Произведение обратных матриц
Матрица, обратная произведению матриц, равна произведению матриц, обратных матрицам-сомножителям, взятому в обратном порядке.
Рассмотрим произведение двух матриц:
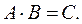
Для того, чтобы найти С–1, умножим обе части равенства слева на В–1А–1, а справа на С–1:
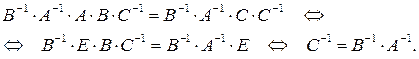
Производная от обратной матрицы
Для значений t, при которых A(t) дифференцируема и существует обратная матрица, производная от A–1(t) имеет вид:
 .
.
Это выражение можно получить, рассматривая
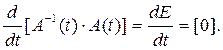
Раскрывая, получим:
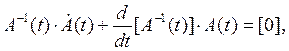
откуда уже окончательно получаем выражение для производной от A–1(t).
Некоторые специальные обратные матрицы
1. Инволютивная матрица.Матрица Аназывается инволютивной, если она совпадает со своей обратной матрицей:
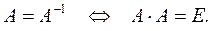
2. Ортогональная матрица. Матрица Аназывается ортогональной, если ее транспонирование равносильно нахождению обратной матрицы:
A–1 = AT.
3. Унитарная матрица.Матрица Аназывается унитарной, если матрица, обратная А, равна матрице, сопряженной с А:

ПРИЛОЖЕНИЕ 2
Некоторые сведения из теории графов
Дата добавления: 2021-09-07; просмотров: 468;











