Линейные и нелинейные модели

Линейными моделями считают такие, для которых выполняется принцип суперпозиции: реакция на суммарное входное воздействие является суммой реакций на каждое из отдельных входных воздействий, составляющих это суммарное.

Такое определение охватывает как статические, так и динамические модели. Применительно к линейным моделям можно также утверждать, что их выход пропорционален входу: чем больше сигнал на входе, тем больше он на выходе. При этом отношение величины выходного сигнала в установившемся режиме к величине входного является коэффициентом пропорциональности.

Так, динамическое уравнение

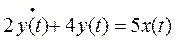
из предыдущего примера является линейной моделью (поскольку и сами переменные x(t), y(t), и их производные – в данном случае y'(t) – входят в уравнение в первой степени). Из этого уравнения можно легко получить статическую модель (статическую характеристику), приравняв производные нулю (так как статическая характеристика – это зависимость выхода от входа в установившемся режиме, т.е. в таком режиме, когда закончены все переходные процессы, а значит, и все изменения переменных). Итак, получаем: 4y = 5x, или y = 1,25x. Коэффициент пропорциональности в данном случае равен 1,25.

Линейную статическую характеристику и прохождение сигналов с выхода на вход безынерционного звена, а также искажение выходного сигнала из-за нелинейной статической характеристики типа «насыщение» иллюстрирует рис. 1.16.

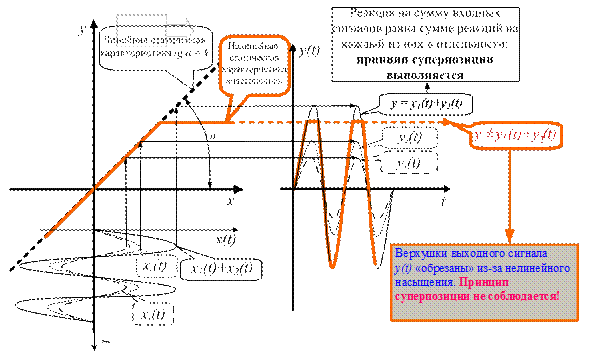Рис. 1.16. Линейная и нелинейная статические характеристики

Однако линейные и нелинейные модели используются не только в технике. Например, в фольклоре разных народов существуют поговорки, изречения, передающие народную мудрость, которые также можно рассматривать в качестве семантических моделей.

Примеры линейных моделей: 1) «Чем дальше в лес, тем больше дров»; 2) «По доходу и расход».

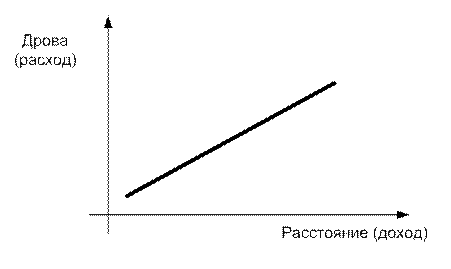
Рис. 1.17. Линейные семантические модели

В двух первых моделях пропорциональная статическая зависимость выхода от входа проиллюстрирована на рис. 1.17.

Примеры нелинейных моделей: 1) «Мал золотник, да дорог»; 2) «Велика фигура, да дура». В двух последних моделях нелинейность выражается в обратной пропорциональности выхода входу и может быть отображена на графике статической характеристики (рис. 1.18).

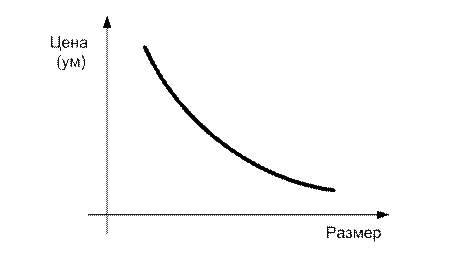
Рис. 1.18. Нелинейные семантические модели

Разумеется, что как линейные, так и разнообразные нелинейные модели находят применение и в других областях. Так, например, в биологии известно, что чем больше вес животного, тем больше пищи оно употребляет для поддержания энергетического баланса (линейная модель) или чем меньше размеры млекопитающего, тем выше у него частота пульса (нелинейная модель) и т.п.

Линейные модели с помощью линейных же преобразований можно трансформировать в другие линейные модели. Например, от модели в виде линейного дифференциального уравнения путем применения линейного интегрального преобразования Лапласа можно перейти к модели в виде передаточной функции. Покажем это на уравнении:

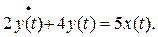
Применим к нему преобразование Лапласа и получим: 2sY(s)+4Y(s)=5X(s), где s – комплексная переменная Лапласа. Далее в левой части вынесем за скобки Y(s) и вспомним из курса ТАУ, что передаточная функция есть отношение преобразованного по Лапласу (при нулевых начальных условиях) выходного сигнала к преобразованному по Лапласу (при тех же условиях) входному сигналу. В результате получим:

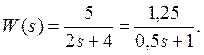
Таким образом, мы получили передаточную функцию апериодического звена с коэффициентом усиления, равным 1,25, и постоянной времени, равной 0,5. При желании можно с помощью линейного преобразования Фурье получить из исходной модели еще одну линейную модель в виде частотных характеристик (из передаточной функции получить ее совсем просто: нужно только произвести замену s=jω). Итак,

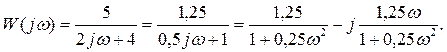
Как правило, реальные объекты и процессы имеют в той или иной степени нелинейный характер, но во многих случаях можно осознанно пренебречь нелинейными свойствами для того, чтобы воспользоваться хорошо разработанным математическим аппаратом исследования линейных моделей для получения предварительных результатов. Однако делать это нужно осторожно, объективно оценивая погрешности и обосновывая возможность такого упрощения.

Так, например, при тщательном описании оказывается, что фактически любые датчики имеют зону нечувствительности – сугубо типовую нелинейность, которая характеризует тот факт, что при очень малых сигналах на входе даже самый чувствительный измерительный прибор на выходе показывает «нуль», означающий отсутствие входного сигнала. Все зависит от величины этой зоны нечувствительности: в некоторых случаях она так мала, что ей можно пренебречь, и тогда модель становится уже линейной.