Классификация видов моделей

<8 9 101112 13 14 >

Рассмотренные выше виды моделей входят в классификацию, приведенную в учебнике [5]. Схема классификации приведена на рис. 1.20.

На схеме темным фоном выделены те виды моделей, которые изучаются в данной дисциплине более подробно.

Особенности использования детерминированных и стохастических, дискретных и непрерывных, статических и динамических, стационарных и нестационарных, распределенных и сосредоточенных моделей были рассмотрены выше.

В зависимости от формы представления оригинала, т.е. средств, используемых при создании моделей, можно выделить идеальное(абстрактное) и реальное моделирование.

Идеальное, или абстрактное моделирование зачастую позволяет исследовать модели объектов, которые практически нереализуемы в заданном интервале времени или не поддаются физическим экспериментам. Идеальное моделирование, как уже говорилось, реализуется посредством сознания человека в виде наглядных,символическихи математическихмоделей.

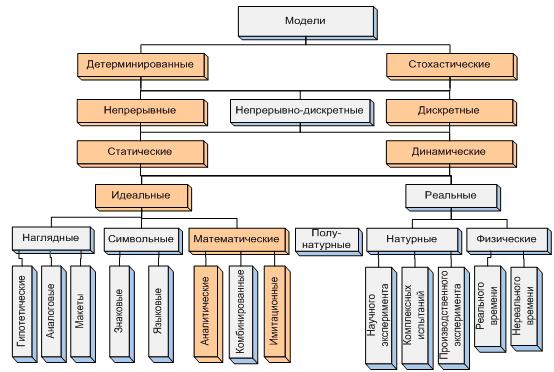
Рис. 1.20. Схема классификации видов идеальных и реальных моделей

Наглядные модели создаются на основе представлений людей о реальных объектах и явлениях и о протекающих в них процессах. При этом гипотетические моделиявляются наименее информативными, опираются на недостаточный для построения формальных моделей уровень знаний исследователя об объекте, отраженный в гипотезах, положенных в основу этих моделей.

Аналоговыемодели используют аналогии разных уровней: от полной аналогии, существующей только для относительно простых объектов, до более низких уровней частных аналогий, охватывающих несколько или даже всего одну сторону функционирования сложного объекта. Идеальные наглядные макетыприменяются в тех случаях, когда процессы, протекающие в реальном объекте, не поддаются физическому моделированию. Для построения идеальных макетов также используются аналогии, как правило, основанные на причинно-следственных связях между процессами и явлениями, происходящими в моделируемом объекте.

Символьныемодели включают знаковыеи языковыемодели, рассмотренные выше (пп. 1.4.7 и 1.4.8). Они представляют собой логические объекты, замещающие реальные объекты-оригиналы и выражающие с помощью определенной системы (алфавита) знаков или символов основные понятия этих оригиналов, а с помощью логических операций – отношения между понятиями.

Математическиемодели представляют собой математические объекты, соответствующие реальным объектам или процессам, конкретный вид которых зависит как от природы реального объекта, так и от задач исследования и требований адекватности и точности их решения. Математические модели подразделяют на аналитические, имитационныеи комбинированные.

Аналитическиемодели характеризуются тем, что процессы функционирования элементов исходной реальной системы записываются в них в виде функциональных соотношений: алгебраических, дифференциальных, интегральных, конечно-разностных и др., а также в виде логических условий. Примером могут служить математические аналитические модели, использующие переменные состояния и аппарат матриц, подробно рассмотренные в п. 2.4 данного учебника. Полученные аналитические модели исследуют следующими методами: 1) аналитическим; 2) численным; 3) качественным.

Аналитический методисследования необходим в том случае, когда нужно получить в общем виде явные зависимости для искомых характеристик. Аналитический метод решения продемонстрирован в примере п. 1.5.4. При невозможности или нецелесообразности решения уравнений в общем виде стремятся получить числовые результаты для конкретных начальных данных, что и приводит к так называемому численному методуисследования. Подобный численный метод решения дифференциальных уравнений рассматривается в гл. 3. Качественный методисследования позволяет даже при отсутствии решения в явном виде определить некоторые важные свойства этого решения, например, его устойчивость.

Как правило, аналитический метод применим к относительно простым объектам и процессам или к упрощенным моделям. Как это было показано, возможно аналитическое решение линейных стационарных дифференциальных уравнений, но это невозможно в общем случае для нелинейных и/или нестационарных дифференциальных уравнений. Численный метод более универсален и позволяет исследовать (по сравнению с аналитическим)более широкий класс систем. Кроме того, он ориентирован на применение компьютеров. Качественные методы анализа используются, например, в теории автоматического управления для оценки эффективности различных вариантов систем управления.

Имитационныемодели отображают все элементарные явления, составляющие моделируемый процесс с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состоянии процесса в определенные моменты времени и оценить характеристики процесса. Основное преимущество имитационного моделирования по сравнению с аналитическимзаключается в возможности решения более сложных задач. Имитационныемодели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные и нестационарные характеристики элементов, разнообразные случайные воздействия и другие, которые создают непреодолимые трудности при аналитических исследованиях. В настоящее время имитационное моделирование представляет собой наиболее эффективный метод исследования сложных и больших систем, а иногда и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования. Более подробно имитационные модели и методы рассмотрены в главе 6.

При реальном моделировании исследование характеристик объекта производится либо полностью на самом реальном объекте, либо частично на реальном объекте, частично на модели. При этом реальный объект может работать как в нормальном режиме, так и в специальных режимах (в ином масштабе времени или при других значениях параметров и переменных). Хотя реальное моделированиеследует признать наиболее адекватным, его возможности весьма ограничены в силу естественных ограничений со стороны реальных объектов. Так, например, проведение реального моделирования сложной автоматизированной системы управления технологическими процессами (АСУТП) потребовало бы прежде всего создания такой системы, а затем проведения экспериментов с управляемыми объектами, т.е. с технологическими процессами, что в большинстве случаев невозможно в условиях реальных действующих предприятий. К тому же в любом случае реальное моделирование обходится чрезвычайно дорого.

Натурныемодели подразумевают использование при исследовании реальных объектов с последующей обработкой результатов эксперимента на основе теории подобия. Такие разновидности натурного эксперимента, как производственный эксперименти комплексные испытания, обладают высокой степенью достоверности. При производственном эксперименте натурное моделирование включает обобщение опыта, накопленного в ходе производственного процесса за счет обработки на базе теории подобия статистического материала по данному процессу и получения его обобщенных характеристик. При комплексных испытаниях повторение испытаний изделий позволяет выявить общие закономерности этих изделий, на основании которых можно судить об их надежности, качестве и других характеристиках.

Научный экспериментотличается широким использованием средств автоматизации при его проведении, разнообразием средств обработки информации и возможностью вмешательства человека в этот процесс.

К реальным моделям относят также и физические модели, которые отличаются от натурных тем, что применяются в исследовательских установках, сохраняющих природу явлений, и обладают физическим подобием. В процессе задаются некоторые характеристики внешней среды, и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях со стороны внешней среды. Физическое моделирование может происходить как в реальном, так и в нереальном масштабе времени, а также и вообще без учета времени («замороженные» процессы).

Вопросы к разделу 1.5