Статические и динамические модели

Статическойназывается модель объекта, отражающая оригинал в какой-то отдельный момент времени, т.е. «моментальная фотография» объекта. Например, буквально фотография или схема.

С фотографией (рис. 1.11) все ясно, что же касается схемы, то даже если это структурная схема с указанием передаточных функций звеньев, по ней явно не видно, как модель изменяется с течением времени (рис. 1.12).

Рис.1.11. Фотография как пример статической модели

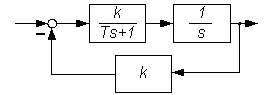
Рис. 1.12. Структурная схема системы

Другой очевидный и знакомый пример статической модели –статическая характеристика, т.е. зависимость выходной переменной объекта (системы) от входной переменной в установившемся режиме, т.е. при t®∞: y(∞)=F[x(∞)] (рис. 1.13).

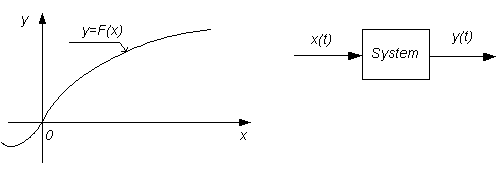
Рис. 1.13. Статическая характеристика системы ”System”

Динамическаямодель, в отличие от статической, учитывает изменения, происходящие в системе с течением времени. Это может выражаться в зависимости входной, выходной и промежуточных переменных от времени. Примером могут служить переходные функции – реакции систем на единичное ступенчатое входное воздействие (рис. 1.14).

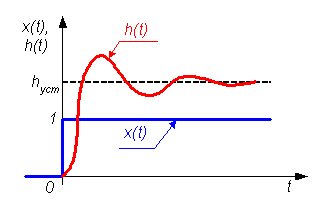
Рис. 1.14. Переходная функция h(t) системы “System”

Обычно переходные функции получаются в результате: 1) аналитического решения; 2) численного интегрирования дифференциальных уравнений, описывающих исследуемую систему; 3) обратного преобразования Лапласа от передаточной функции системы, деленной на s. Модельв виде дифференциальных уравнений (ДУ) является широко распространенной динамической моделью.

Пример. Пусть система описывается моделью в виде дифференциального уравнения: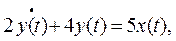

входное воздействие x(t)=1[t] – единичное ступенчатое (как на рис. 1.14), а начальные условия имеют вид: y(t=0) = 0, т.е. процесс начинается из начала координат.

Аналитическое решение. Это линейное дифференциальное уравнение первого порядка с постоянными коэффициентами (стационарное). Его решение складывается из двух слагаемых – общего и частного решения:

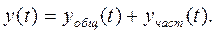
Общее решение ищется в виде:

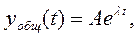
где А – неизвестный коэффициент, определяемый из начальных условий;

l – корень характеристического уравнения, которое в данном случае выглядит так:

,

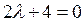откуда l=–2.

В стандартной форме исходное уравнение должно иметь при y(t) коэффициент, равный единице. Для этого исходное уравнение разделим на 4 и получим:

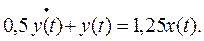
Частное решение зависит от вида правой части ДУ; в данном примере, поскольку x(t)=1[t], частное решение будет равно константе:

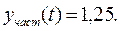
Суммарное решение будет выглядеть так:

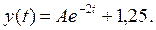
Теперь, подставив в решение y(t) начальное условие (для уравнения 1-го порядка оно одно), можно найти значение коэффициента А:

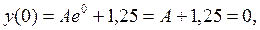
откуда А = –1,25. Окончательно решение имеет вид:

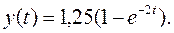
Поскольку входным воздействием было единичное ступенчатое, то полученное решение является переходной функцией и обозначается, как обычно, h(t). График этой функции показан на рис. 1.15.

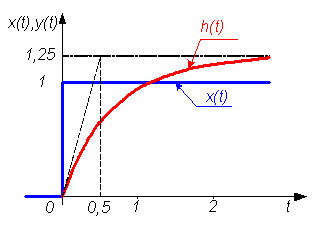
Рис. 1.15. Переходная функция h(t) – решение ДУ из примера

Подобный h(t) характер (с разной погрешностью) имеют такие процессы, как разгон автомобиля, нагрев жидкости, накопление знаний в некоторой предметной области, увеличение численности популяции животных, рост производства (при определенных условиях) и многие другие. В этом заключается одно из важнейших свойств математическихмоделей – их универсальность.