Теорема об изменении количества движения системы

Теорема об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему:

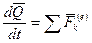. (163)

В проекциях на прямоугольные декартовы оси координат

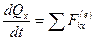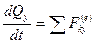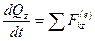, , . (163')

т. е. производная по времени от проекции количества движения системы на какую-либо координатную ось равна сумме проекций всех внешних сил системы на ту же ось.

Теорема импульсов для системы в дифференциальной форме: дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему.

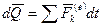. (164)

В проекциях на координатные оси эта теорема примет вид:

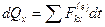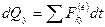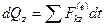, , . (164')

Теорема импульсов для системы в конечной или интегральной форме: изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время.

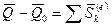, (165)

где 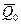– количество движения системы в момент 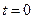; 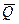– количество движения в момент 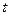; 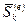– импульс внешней силы, действующей на 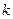-ю точку за время ; .

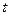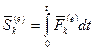В проекциях на прямоугольные оси имеем:

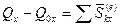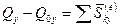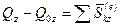, , . (165')

Внутренние силы системы не входят явно в теорему об изменении количества движения системы в любой из форм и, следовательно, не влияют непосредственно на изменение количества движения системы. Они могут влиять на изменение количества движения только неявно через внешние силы.