Моменты инерции относительно точки и оси
 Моментом инерции механической системы, состоящей из
Моментом инерции механической системы, состоящей из 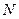 материальных точек, относительно точки
материальных точек, относительно точки 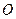 называется сумма произведений масс этих точек на квадраты их расстояний до точки
называется сумма произведений масс этих точек на квадраты их расстояний до точки 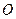 (рис. 51), т. е.
(рис. 51), т. е.
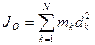 . (139)
. (139)
 Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем:
Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем:
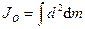 , (139')
, (139')
где 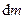 – масса элементарной частицы тела (в пределе точка);
– масса элементарной частицы тела (в пределе точка); 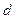 – ее расстояние до точки
– ее расстояние до точки 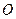 .
.
Моментом инерции 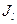 системы материальных точек относительно оси
системы материальных точек относительно оси 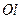 называется сумма произведений масс этих точек на квадраты их расстояний
называется сумма произведений масс этих точек на квадраты их расстояний 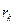 до оси
до оси 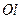 (рис. 51):
(рис. 51):
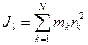 . (140')
. (140')
В частном случае сплошного тела сумму следует заменить интегралом:
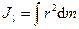 , (140')
, (140')
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 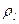 , относительно оси
, относительно оси 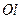 определяется но формуле
определяется но формуле
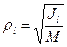 , (141)
, (141)
где 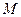 – масса тела.
– масса тела.
Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением
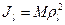 , (141')
, (141')
В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.
Дата добавления: 2017-09-01; просмотров: 1346;











