Векторная диаграмма и схема замещения катушки с сердечником
При расчете цепей с ферромагнитными элементами с синусоидальными источниками питания индуктивность L нельзя считать постоянной, и поэтому необходимо использовать зависимость между ЭДС и потокосцеплением или потоком. Форма кривой зависимости между потоком Ф и намагничивающим током i (рис. 4.8) подобна форме основной кривой намагничивания В(Н), т.к. Ф = B S, а H = IW / L.
Нелинейный характер зависимости между Ф и i приводит к тому, что индуктивность катушки L = W Ф / i перестает быть величиной постоянной и зависит от величины намагничивающего тока.
При непостоянстве индуктивности L ЭДС самоиндукции е, наводимую в катушке переменным током i следует определять по формуле
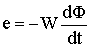 .
.
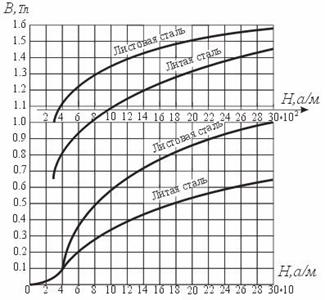
Рис. 4.8. Зависимость В(Н)
Если к катушке подведено синусоидальное напряжение u = Um sin(ωt + π/2), а активное сопротивление обмотки R ≈ 0, то приложенное напряжение уравновешивается только ЭДС самоиндукции:
u = -e,
Um sin(ωt + π/2) = W dФ / dt.
Интегрируя это выражение, получим
Ф = Um / (2 π f) W sin(ωt) = Фm sin(ωt).
Из полученного соотношения следует:
1. При синусоидальном напряжении на зажимах катушки магнитный поток Ф, вызванный протекающим по цепи током I, тоже синусоидальный.
2. Заданному действующему значению напряжения U на зажимах катушки соответствует определенная амплитуда магнитного потока Фm независимо от того, имеется ли у катушки стальной сердечник или же магнитный поток целиком замыкается по воздуху. Магнитный поток индуктирует в обмотке катушки ЭДС самоиндукции е, равную по величине приложенному напряжению и противоположную ему по направлению
e = -W dФ/dt = -W Фm ω cos(ωt) = 2 π f W Фm sin(ωt - π/2),
Em = 2 π f W Фm,
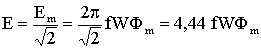 .
.
При этом индуктируемая ЭДС Е отстает от магнитного потока на четверть периода.
Выражение для действующей индуктированной ЭДС E = 4,44 f W Фmчасто используется при анализе работы и в практических расчетах и называется трансформаторной ЭДС.
Процесс намагничивания и размагничивания стального сердечника протекает по несовпадающим ветвям петли гистерезиса. График зависимости Ф(i) при циклическом перемагничивании (рис. 4.9 а) имеет такую же форму, как и петля гистерезиса В(Н). На рис. 4.9 б изображен график синусоидального изменения магнитного потока во времени Ф(t).
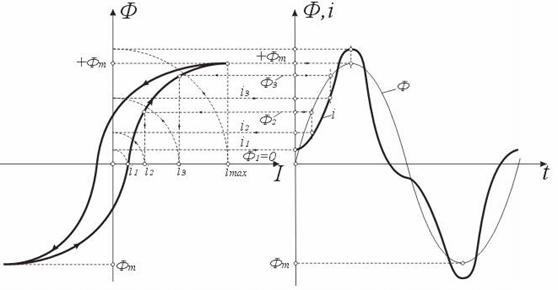
а) б)
Рис. 4.9. Кривая перемагничивания (а) и кривые Ф(t) и Ф(i) для катушки со стальным сердечником
Располагая кривыми Ф(i) и Ф(t), построим кривую намагничивающего тока i(t).
Полученная кривая намагничивающего тока i(t) является несинусоидальной периодической функцией. Для упрощения анализа и расчета цепей переменного тока, содержащих катушки с ферромагнитными сердечниками, несинусоидальный намагничивающий ток заменяют эквивалентным синусоидальным, опираясь на равенство действующих значений. Для построения расчетной схемы замещения катушки с сердечником запишем уравнение
u = -e + Lр di / dt + R i ,
где: R – сопротивление обмотки;
Lр – индуктивность рассеяния.
Полное комплексное сопротивление запишется
Z = R + Ro + i (xр + xo),
где: Ro – активное сопротивление, обусловлено потерями на вихревые токи и гистерезис;
xo – индуктивное сопротивление, определяет мощность, необходимую на создание основного магнитного потока;
R – сопротивление обмотки катушки;
xр – индуктивное сопротивление, определяет мощность потока рассеяния;
Ro и xo – нелинейные сопротивления.
Векторная диаграмма и а) последовательная, б) параллельная схемы замещения изображены на рисунке 4.10.
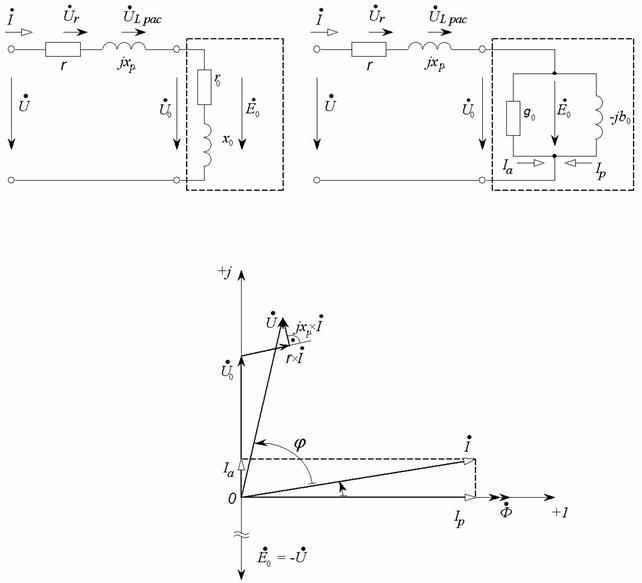
Рис. 4.10. Векторная диаграмма и соответствующие ей а) последовательная и б) параллельная схемы замещения
Дата добавления: 2018-05-10; просмотров: 2299;











