Вычисление моментов инерции относительно осей параллельных центральным осям.
Оси 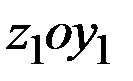 параллельны центральным осям
параллельны центральным осям 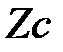 ,
, 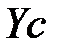 (рис.1.8). Для произвольной точки
(рис.1.8). Для произвольной точки 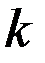 имеем:
имеем: 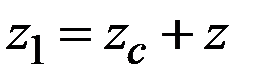 ;
; 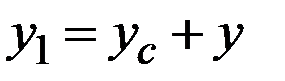 . Тогда
. Тогда
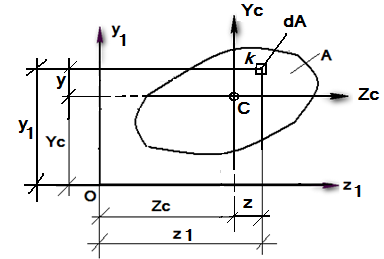
Рис.1.8
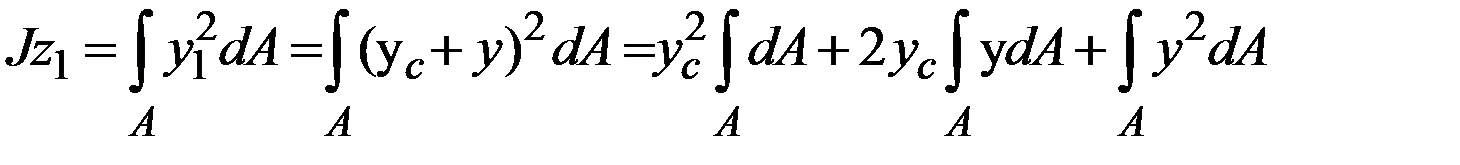 .
.
Таким образом, имеем 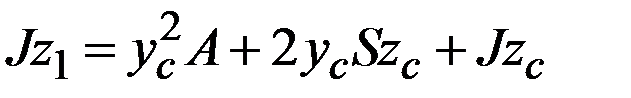 . Так как ось
. Так как ось 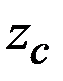 центральная (
центральная ( 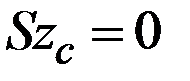 ) , то окончательно получим
) , то окончательно получим 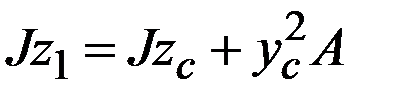 . Проводя аналогичные выкладки, будем иметь:
. Проводя аналогичные выкладки, будем иметь:
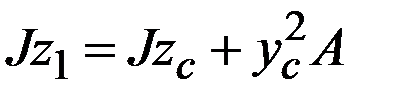
| 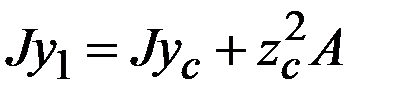
|
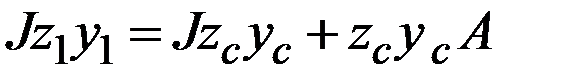
| (1.8) |
Для полярного момента инерции
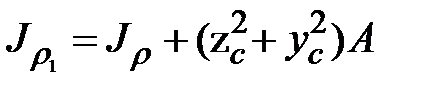 . .
| (1.9) |
Пример 1.1 Найти осевые и центробежный моменты инерции прямоугольника относительно осей 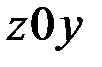 (рис.1.9,а) и относительно центральных осей
(рис.1.9,а) и относительно центральных осей 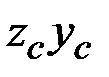 (рис.1.9,б)
(рис.1.9,б)
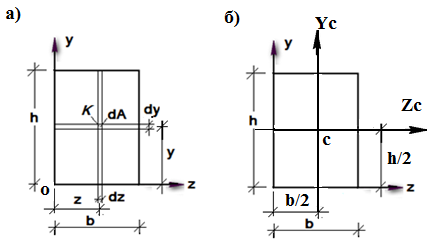
Рис. 1.9 Прямоугольник
Зафиксируем произвольную точку 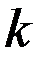 прямоугольника координатами
прямоугольника координатами 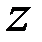 ,
, 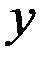 . Вблизи точки
. Вблизи точки 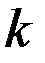 выделим элементарную площадку площадью
выделим элементарную площадку площадью 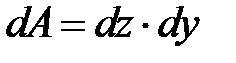 .
.
Момент инерции элементарной площадки относительно оси 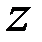 равен
равен 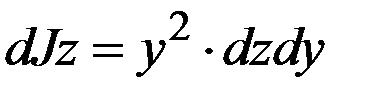 . Момент инерции элементарной горизонтальной полоски равен
. Момент инерции элементарной горизонтальной полоски равен 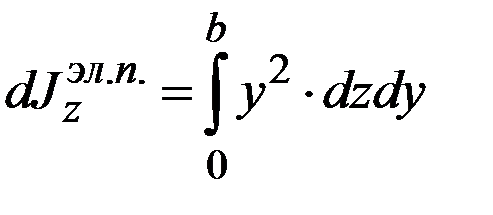 . Тогда момент инерции прямоугольника равен сумме по высоте сечения элементарных моментов инерции горизонтальных полосок, т.е.
. Тогда момент инерции прямоугольника равен сумме по высоте сечения элементарных моментов инерции горизонтальных полосок, т.е. 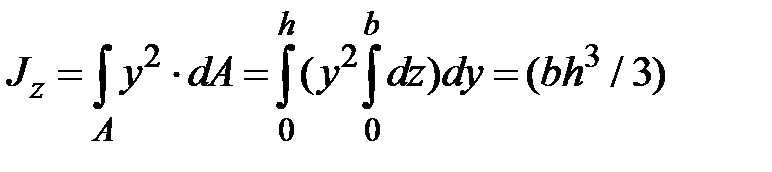 . Аналогично
. Аналогично
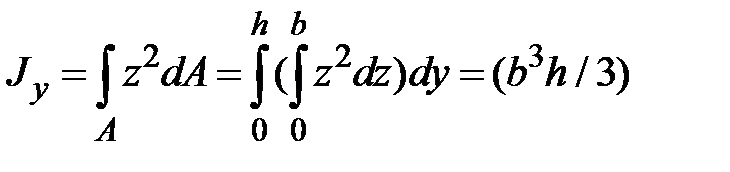 ;
; 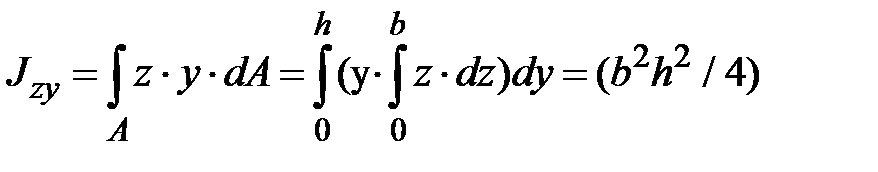 .
.
Для осевых и центробежного моментов инерции прямоугольника относительно осей проходящих через его стороны имеем:
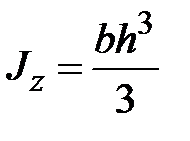
| 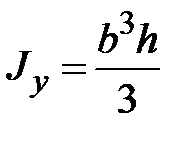
| 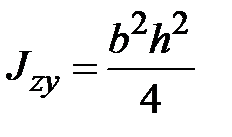
| (1.10) |
Осевые и центробежный моменты инерции относительно центральных осей, в соответствии с формулами (1.8), примут вид:
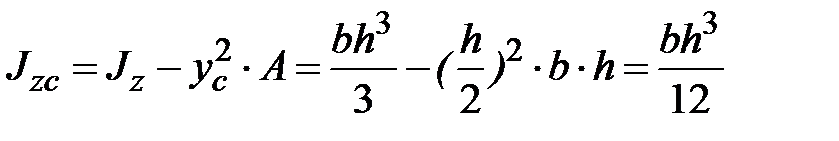 ;
;
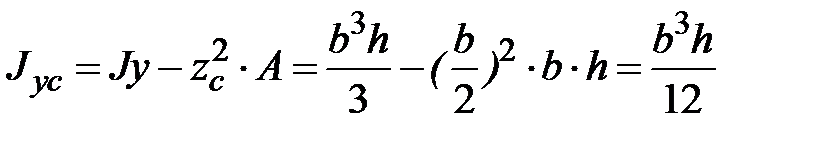 ;
;
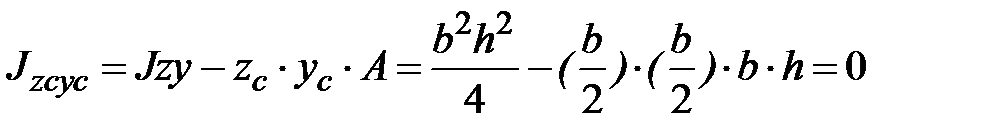 .
.
Осевые и центробежный моменты инерции относительно центральных осей:
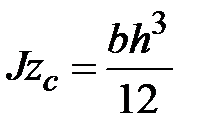 , ,
| 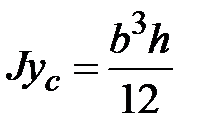 , ,
|
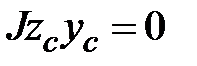 . .
| (1.11) |
Пример 1.2 Определить полярный моменты инерции круга, моменты инерции круга, полукруга, четверти круга относительно центральных осей 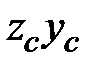 ;
; 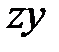 (рис.1.10).
(рис.1.10).
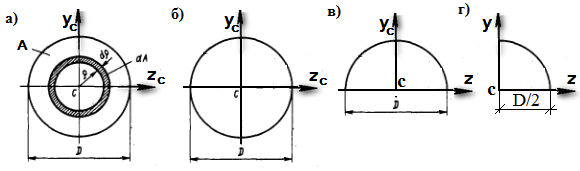
Рис.1.10 К примеру 1.2
Сначала определим полярный момент инерции, а затем, учитывая равенство (1.6) 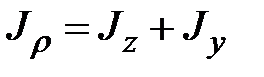 и то, что
и то, что 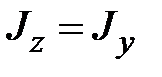 найдем
найдем 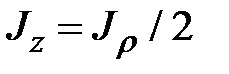 .
.
Разобьем круг на бесконечно тонкие кольца толщиной 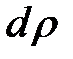 радиусом
радиусом 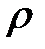 ; площадь такого кольца
; площадь такого кольца 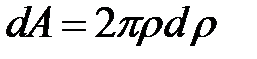 (рис.1.10,а). Далее суммируем элементарные полярные моменты колец вдоль радиуса, получим
(рис.1.10,а). Далее суммируем элементарные полярные моменты колец вдоль радиуса, получим 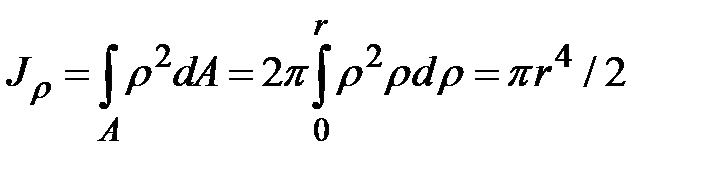 .
.
Окончательно полярный момент инерции для круга 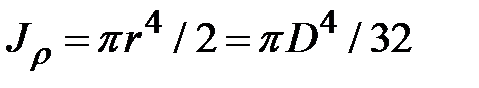 .
.
Осевые моменты инерции, для круга (рис.1.10,б) 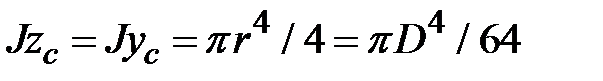 .
.
Для полукруга (рис.1.10,в) 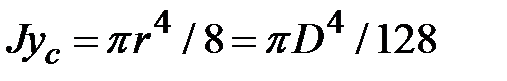 .
.
Для четверти круга (рис.1.10,г) 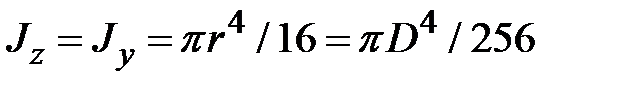 .
.
Дата добавления: 2017-09-01; просмотров: 2280;











