Главные оси и главные моменты инерции. Радиус инерции. Эллипс инерции.
Оси, относительно которых центробежный момент равен нулю, называются главными.
Если главные оси проходят через центр тяжести сечения, то оси называются главными центральными осями.
Моменты инерции относительно этих осей называются главными моментами инерции или главными центральными моментами инерции.
Главными осями являются такие две взаимно перпендикулярные оси, относительно которых центробежный момент равен нулю, а осевые моменты инерции принимают максимальное и минимальное значения.
Пусть известны моменты инерции сечения: 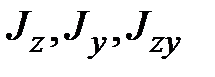 .
.
Обозначим через 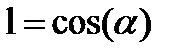 ,
, 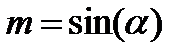 направляющие косинусы оси u,тогда выражение (1.15) можно записать в виде
направляющие косинусы оси u,тогда выражение (1.15) можно записать в виде
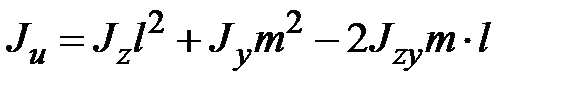
| (1.18) |
Введем в рассмотрение матрицу и вектор:
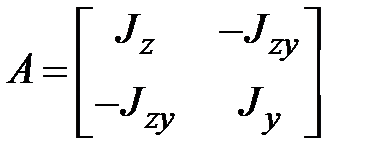 ; ; 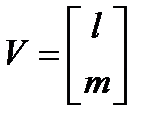 ; ; 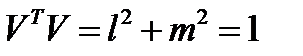 . .
| (1.19) |
Рассмотрим функцию 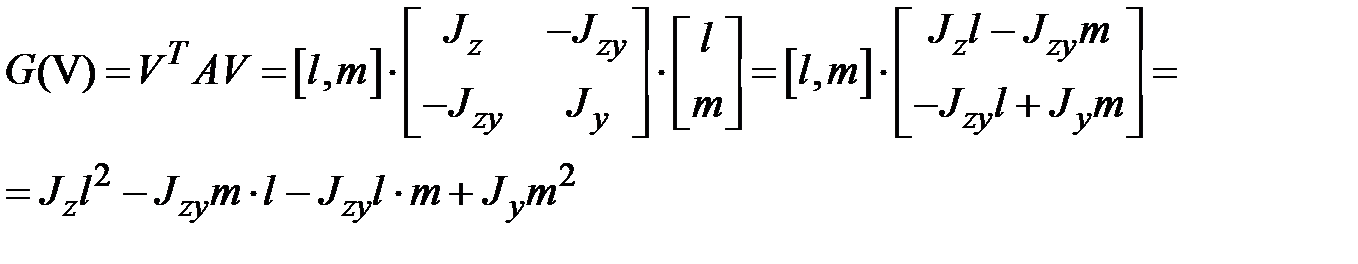
Таким образом, получим
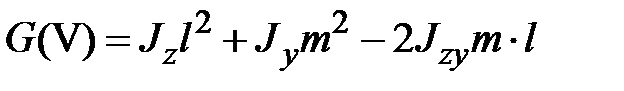 . .
| (1.20) |
Правые части выражений (1.18) и (1.20) одинаковые, следовательно, получаем
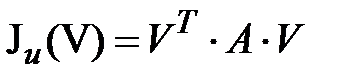
| (1.21) |
Рассмотрим задачу на собственные значения для матрицы 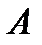 (см.(1.19))
(см.(1.19))
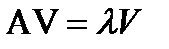 . .
| (1.22) |
Обозначим через 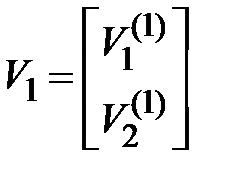 , -собственный вектор и соответствующее ему наименьшее собственное число
, -собственный вектор и соответствующее ему наименьшее собственное число 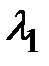 матрицы
матрицы 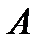 , а через
, а через 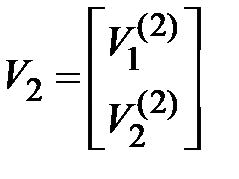 , собственный вектор и соответствующее ему наибольшее собственное число
, собственный вектор и соответствующее ему наибольшее собственное число 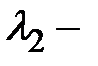 матрицы
матрицы 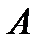 , т.е.
, т.е.
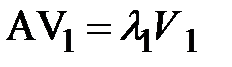 , , 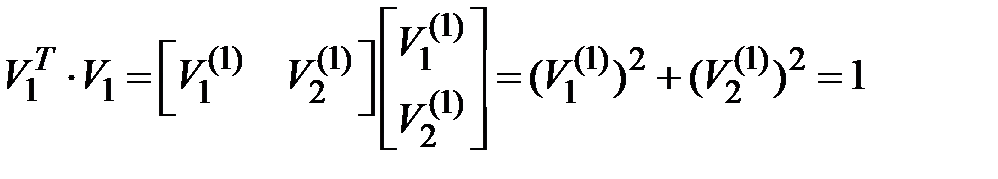 , ,
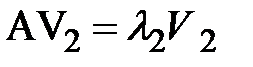 , , 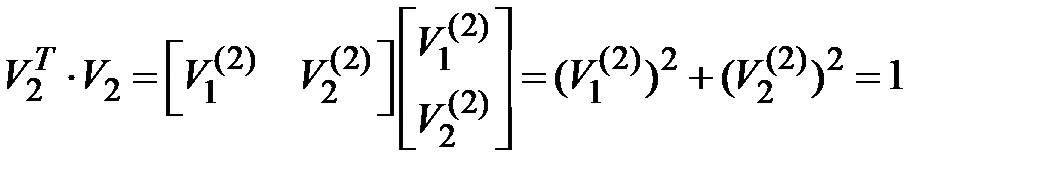 , ,
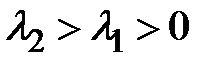 . .
| (1.23) |
Так как матрица 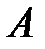 симметричная и положительно определена (
симметричная и положительно определена ( 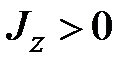 ,
, 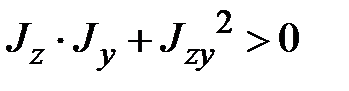 ), то собственные значения
), то собственные значения 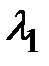 ,
, 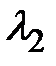 -положительные действительные числа, а векторы
-положительные действительные числа, а векторы 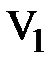 и
и 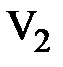 линейно независимы и ортогональны
линейно независимы и ортогональны
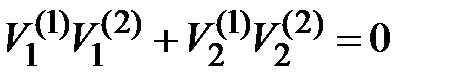 . .
| (1.24) |
Для собственных векторов матрицы 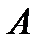 имеем
имеем
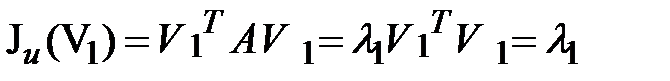 ; ;
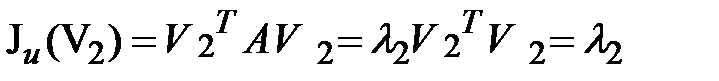
| (1.25) |
Собственные числа матрицы 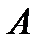 определяются из уравнения
определяются из уравнения
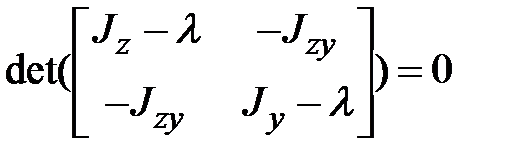 .
.
Раскрываем определитель, получаем
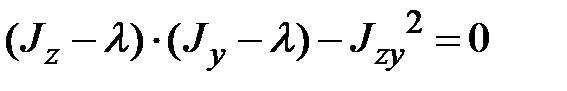 , или после раскрытия скобок имеем квадратное уравнение
, или после раскрытия скобок имеем квадратное уравнение
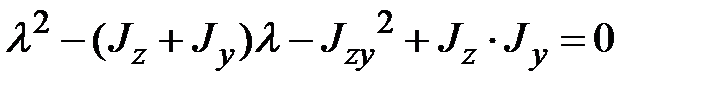
| (1.26) |
Корни квадратного уравнения определяются по формулам:
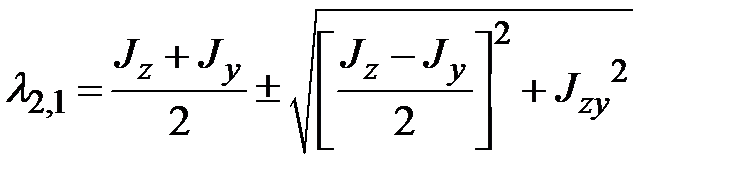 . .
| (1.27) |
Формулы (1.27) для наибольшего собственного числа 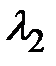 и наименьшего собственного числа
и наименьшего собственного числа 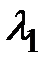 матрицы
матрицы 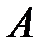 полностью совпадают с известными формулами для главных моментов инерции [1]
полностью совпадают с известными формулами для главных моментов инерции [1]
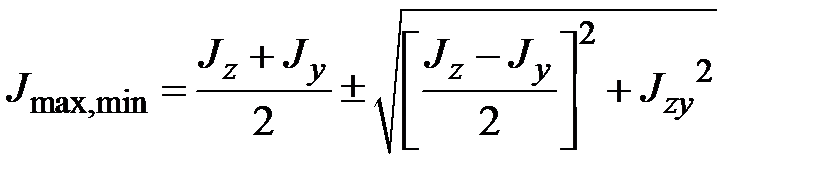
| (1.28) |
Таким образом, минимум функции 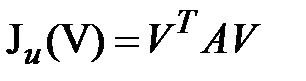 достигается на собственном векторе
достигается на собственном векторе 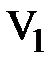 и он численно равен
и он численно равен 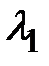 , а максимум достигается на собственном векторе
, а максимум достигается на собственном векторе 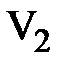 и он численно равен
и он численно равен 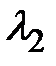 .
.
Собственные векторы матрицы 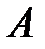 (направляющие косинусы главных осей инерции) определяются из решения систем линейных однородных алгебраических уравнений
(направляющие косинусы главных осей инерции) определяются из решения систем линейных однородных алгебраических уравнений 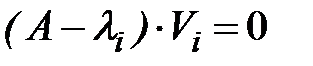 ,
, 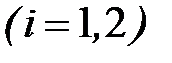 . Так как определитель системы равен нулю, то первое уравнение можно отбросить, а из второго найти отношение координат собственного вектора
. Так как определитель системы равен нулю, то первое уравнение можно отбросить, а из второго найти отношение координат собственного вектора 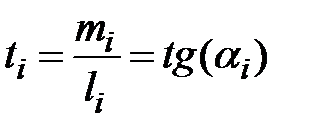 , а затем и сами координаты:
, а затем и сами координаты: 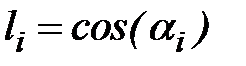 ;
; 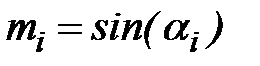 .
.
Ниже представлены расчетные формулы:
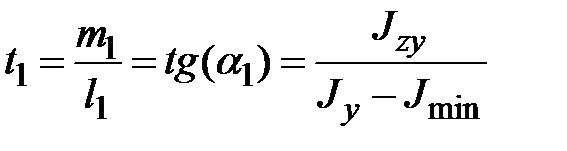 , , 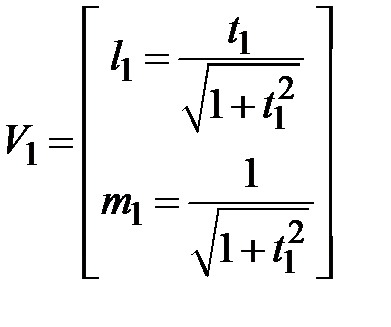 ; ;
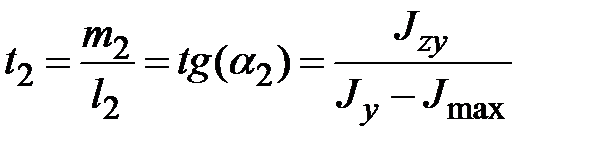 , , 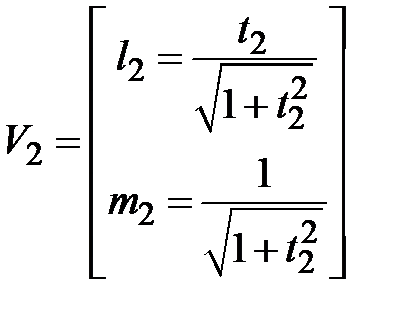 . .
| (1.29) |
Покажем, что углы, найденные из уравнений (1.29), обращают выражение для центробежного момента (1.17) в нуль.
Приравниваем выражение (1.17) нулю и из уравнения
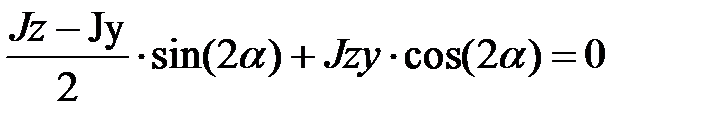 , находим
, находим 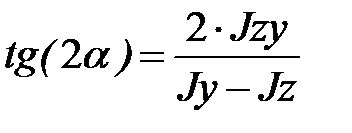 . Тангенс двойного аргумента выразим через тангенс одинарного аргумента
. Тангенс двойного аргумента выразим через тангенс одинарного аргумента 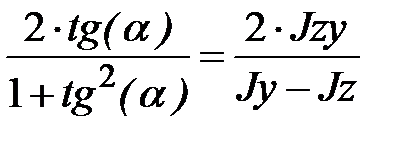 . Введем замену
. Введем замену 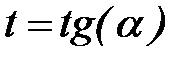 , тогда последнее уравнение примет вид
, тогда последнее уравнение примет вид 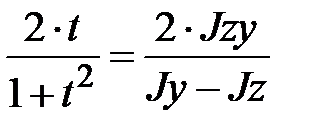 . Решаем квадратное уравнение относительно
. Решаем квадратное уравнение относительно 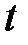 , получаем
, получаем
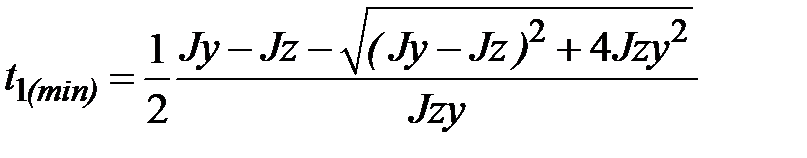 ;
; 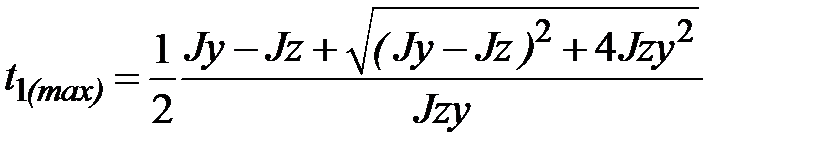 .
.
В исходных обозначениях:
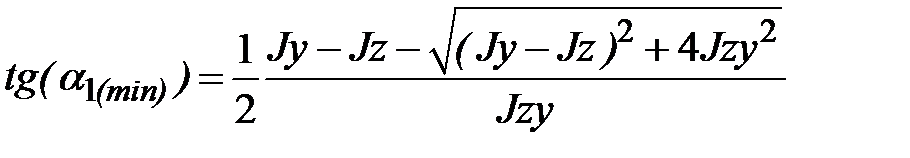 , ,
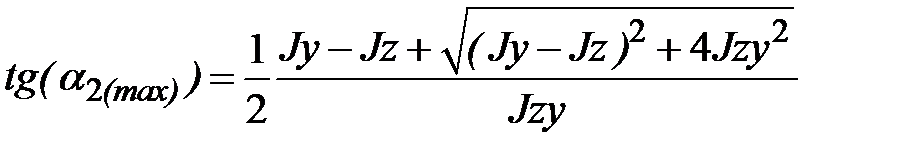 . .
| (1.30) (1.31) |
Приравниваем правые части выражений (1.29) и (1.30), получаем
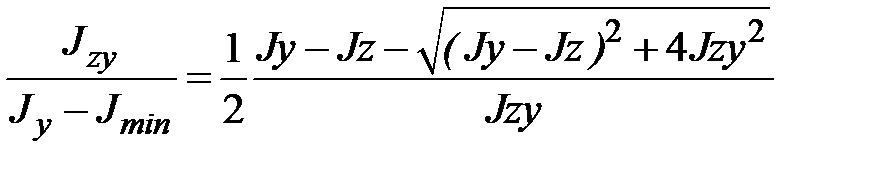 .Подставляем в последнее выражение
.Подставляем в последнее выражение
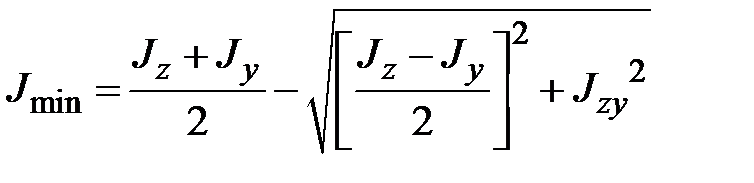 . После несложных преобразований приходим к тождеству
. После несложных преобразований приходим к тождеству 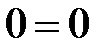 . Аналогичное доказательство для
. Аналогичное доказательство для 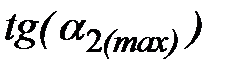 .
.
Важной геометрической характеристикой поперечного сечения стержня являются максимальный и минимальный радиусы инерции. Эти геометрические характеристики используются в теории устойчивости стержней и определяются по формулам:
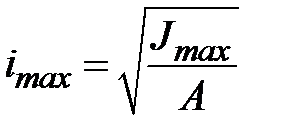 , , 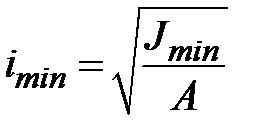 . .
| (1.32) |
Пример 1.6 Прямоугольный равнобедренный треугольник со сторонами 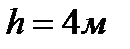
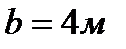 (рис.2). Вычислим главные моменты инерции и положение главных центральных осей инерции:
(рис.2). Вычислим главные моменты инерции и положение главных центральных осей инерции:
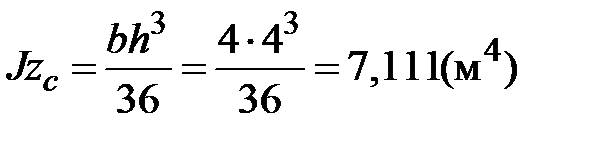 ,
, 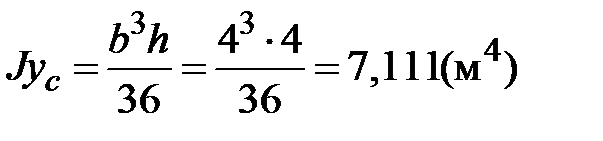 ,
, 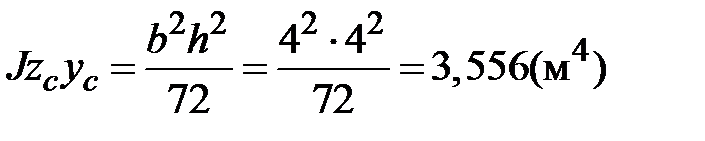 ;
; 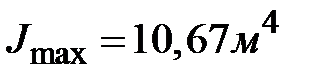 ,
, 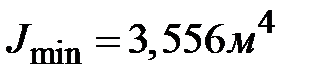 ,
,
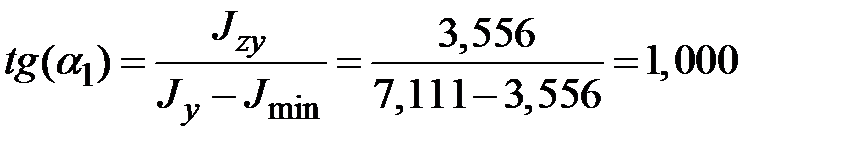 ,
, 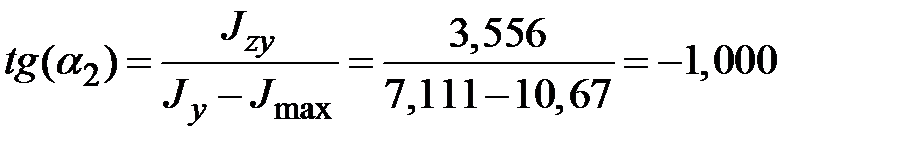
Угол между осью 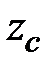 и главной осью инерции, относительно которой момент инерции минимален, равен
и главной осью инерции, относительно которой момент инерции минимален, равен 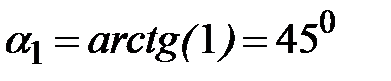 (рис. 1.17,б).
(рис. 1.17,б).
Угол между осью 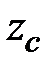 и главной осью инерции, относительно которой момент инерции максимален, равен
и главной осью инерции, относительно которой момент инерции максимален, равен 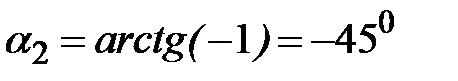 (рис. 1.17,б).
(рис. 1.17,б).
Направляющие косинусы главных осей инерции (рис.1.17,а)
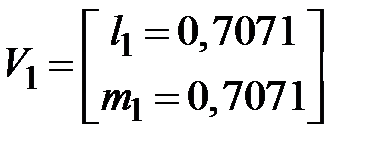 ; ,
; , 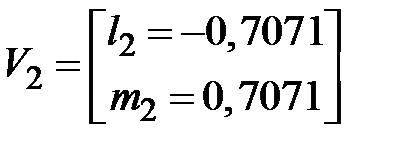 .
.
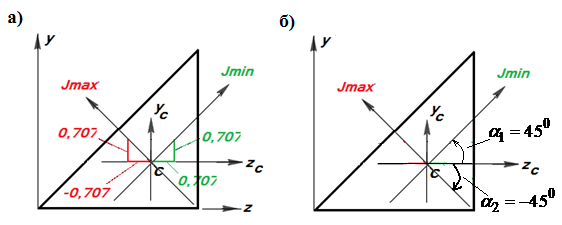
Рис.1.17 К определению главных центральных осей инерции
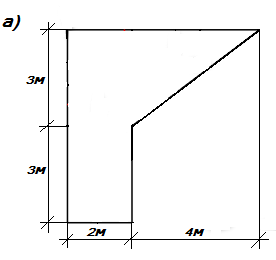
Пример 1.7Определим центр тяжести сложного сечения, состоящего из двух фигур (рис.1.18,а).
Статические моменты сложного сечения, разбитого на простейшие части (рис.1.18,a), для которых известны площади 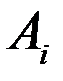 и положение центра тяжести
и положение центра тяжести 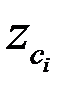 ,
, 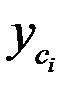 определяются по формулам:
определяются по формулам:
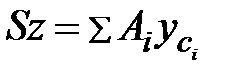 , ,
| 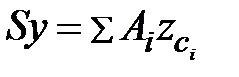 . .
| (1.31) |
Начало координат примем в т.О. Исходную фигуру разобьем на две простые: прямоугольник и треугольник. Площадь прямоугольника и его координаты центра тяжести: 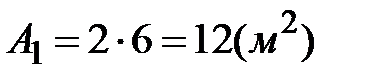 ;
; 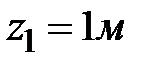 ;
; 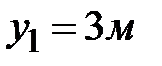 . Площадь треугольника и его координаты центра тяжести:
. Площадь треугольника и его координаты центра тяжести: 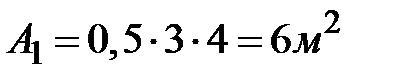 ;
; 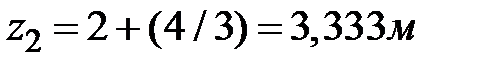 ;
; 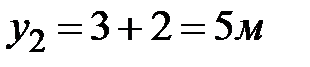 . Площадь сложной фигуры
. Площадь сложной фигуры 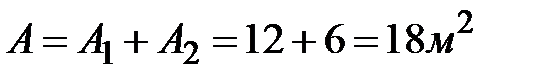
Статические моменты: 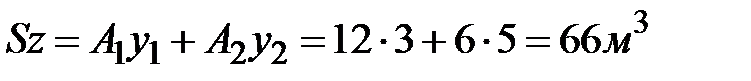 ;
;
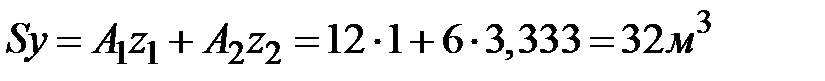 .
.
Координаты центра тяжести: 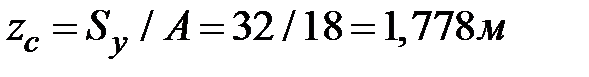 ;
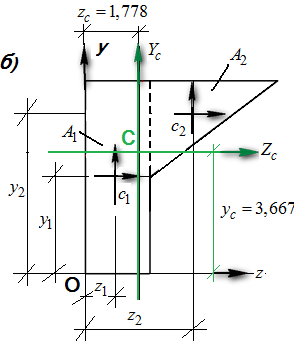
; 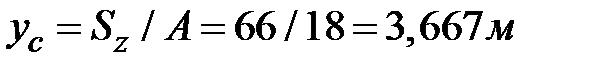 . Центральные оси фигуры показаны на рис. 1.18,б.
. Центральные оси фигуры показаны на рис. 1.18,б.
Сделаем проверку найденных координат центра тяжести. Статические моменты относительно центральных осей равны нулю ( 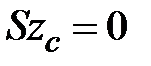 ,
, 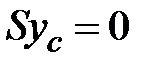 ).
).
Вычислим координаты центров тяжести прямоугольника и треугольника относительно центральных осей всей фигуры: 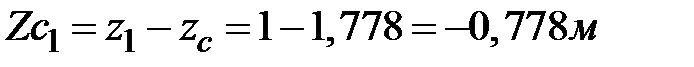 ;
; 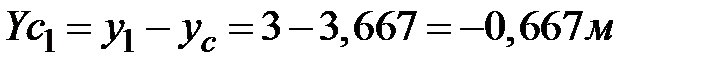 ;
;
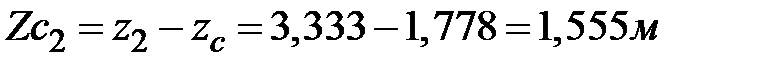 ;
; 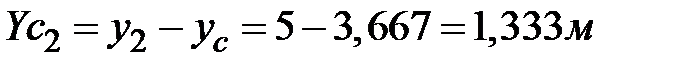 ;
;
| 
|
Рис. 1.18 Сложное сечение из двух фигур
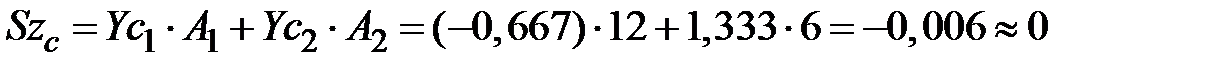 ;
;
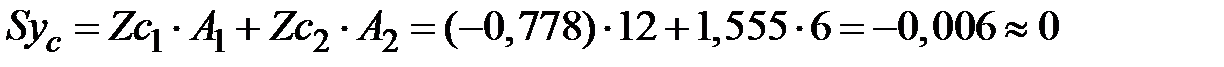 .
.
Координаты центров тяжести определены верно (погрешность соответствует правилу округления, применяемому при вычислениях).
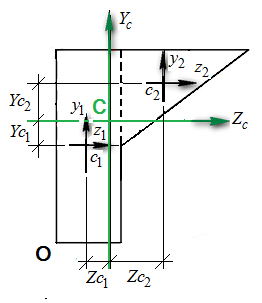
Рис. 1.19 К вычислению моментов инерции
Вычислим значения осевых и центробежного моментов сложной фигуры рис.1.19
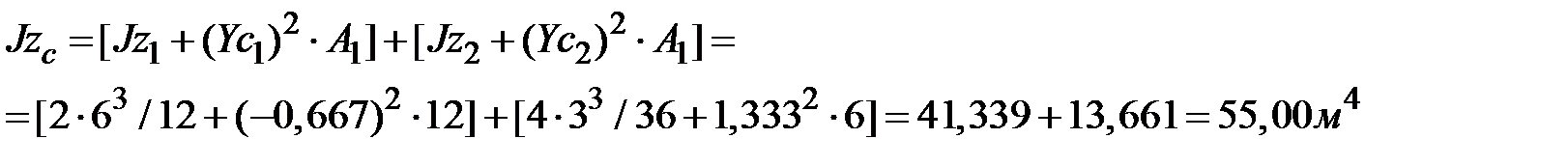
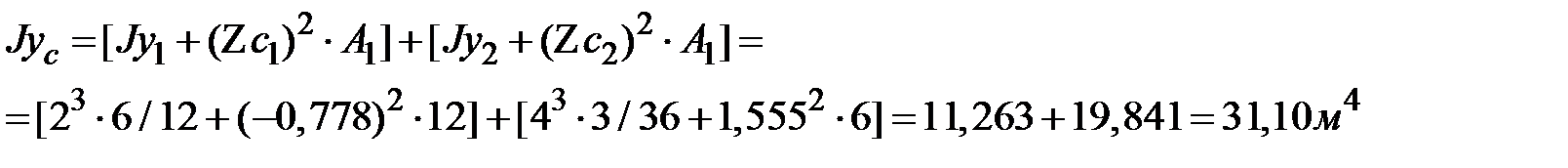
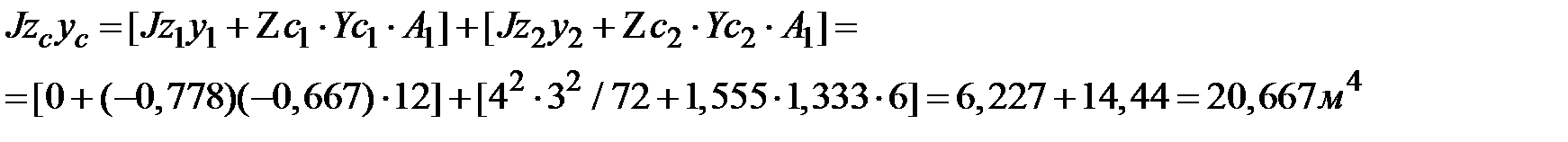 Имеем :
Имеем : 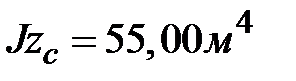 ;
; 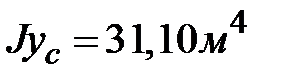 ;
; 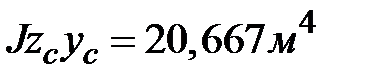 .
.
Определим главные центральные оси и главные моменты инерции.
По формулам(1.28) получим: 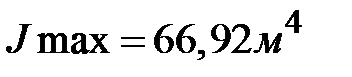 ;
; 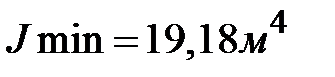 .Радиусы инерции
.Радиусы инерции 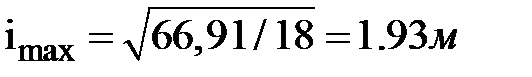 ;
; 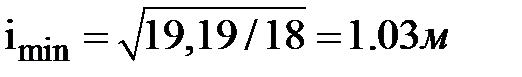 .
.
Углы наклона главных осей инерции к оси 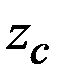
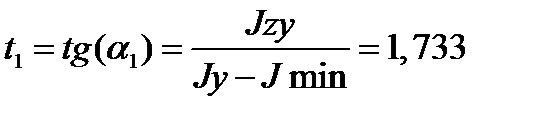 ;
; 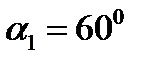 .
. 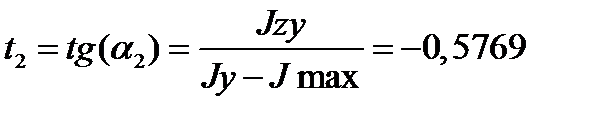 ;
; 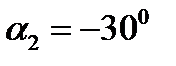 .
.
Углы откладываются с помощью транспортира.
Направляющие косинусы оси 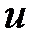 , относительно которой момент инерции минимален (
, относительно которой момент инерции минимален ( 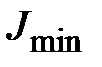 )
) 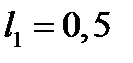 ;
; 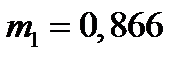 .
.
Направляющие косинусы оси 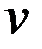 , относительно которой момент инерции максимален (
, относительно которой момент инерции максимален ( 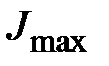 )
) 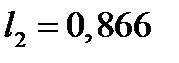 ;
; 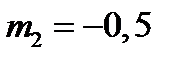 .
.
Направляющие косинусы откладываются с помощью линейки.
| 
|
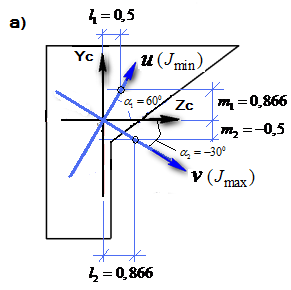
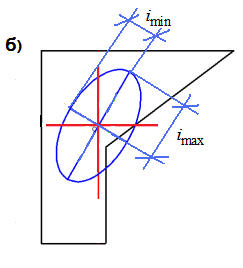
Рис.1.20 Главные центральные оси и эллипс инерции
Вычисляем радиусы инерции 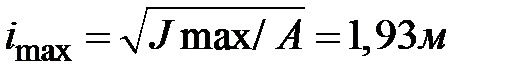 ,
, 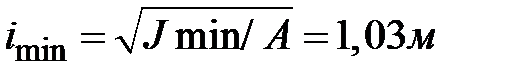 , строим эллипс инерции (рис.1.20,б)
, строим эллипс инерции (рис.1.20,б)
С помощью эллипса инерции можно определить момент инерции относительно произвольной оси графическим способом.
Таблица 1
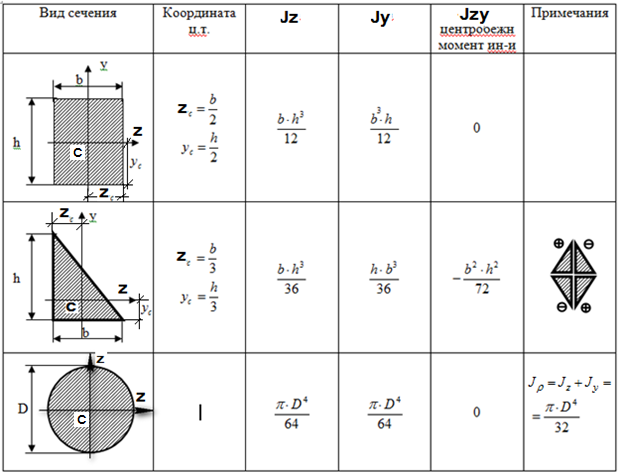

ПРИЛОЖЕНИЕ 1.1
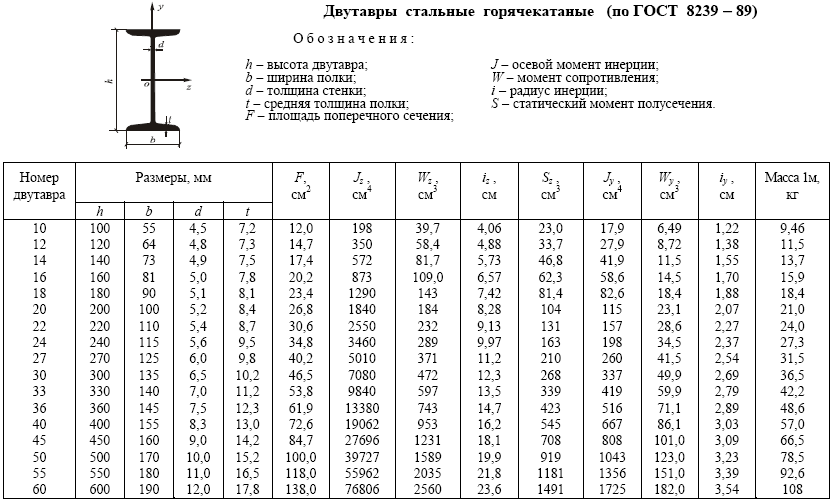
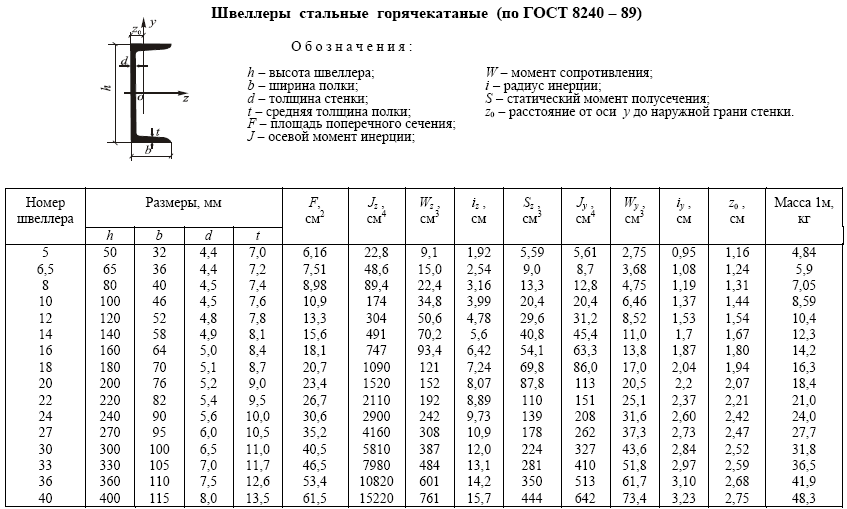
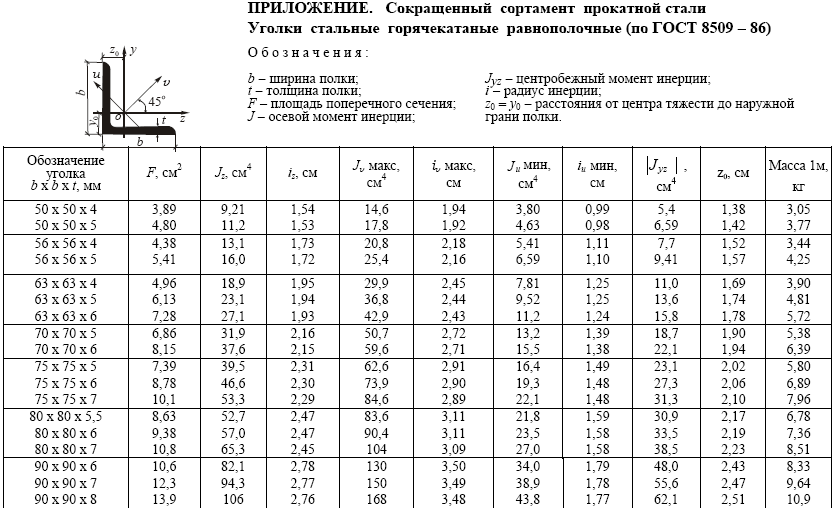
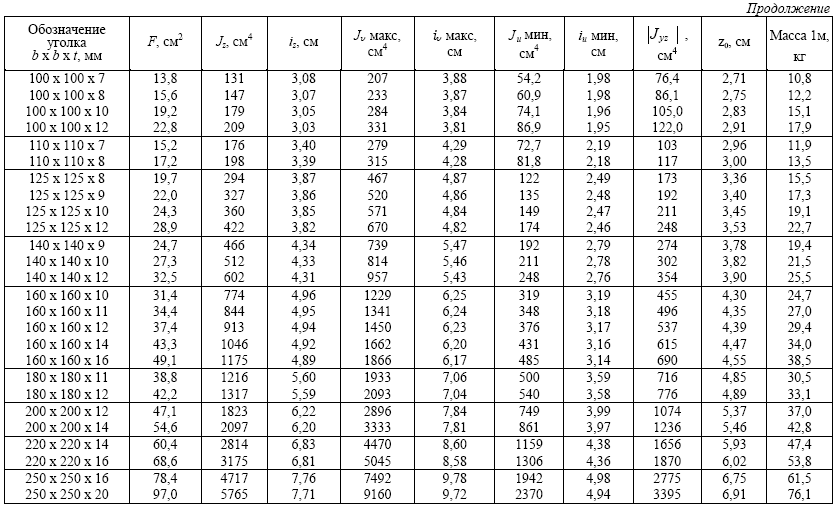
ПРИЛОЖЕНИЕ 1.2
Для вычисления геометрических характеристик поперечных сечений удобно использовать систему инженерных расчетов 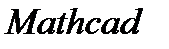 . Ниже представлен код программы, реализующий вычисление геометрических характеристик простых фигур с помощью интегралов (1.12; 1.13)
. Ниже представлен код программы, реализующий вычисление геометрических характеристик простых фигур с помощью интегралов (1.12; 1.13)

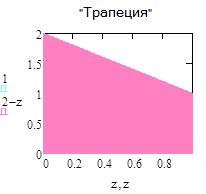
Name:=”Треугольник”



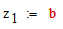
Программный модуль

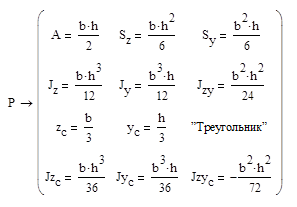
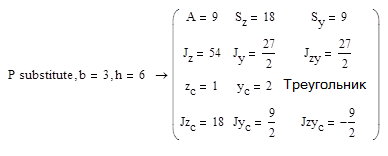
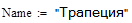
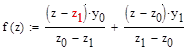











Дата добавления: 2017-09-01; просмотров: 5087;











