Геометрические характеристики криволинейной трапеции.

Если поперечное сечение задается как плоская фигура, ограниченная кривой 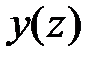на отрезке 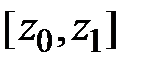(рис.1.11), то площадь и статические моменты сечения можно вычислять, используя обычные интегралы. Рассмотрим плоскую фигуру ограниченную функцией 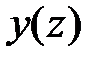на отрезке 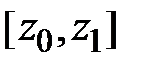(рис.1.11)

Площадь и статические моменты определяются по известным из курса высшей математики формулам [1]:

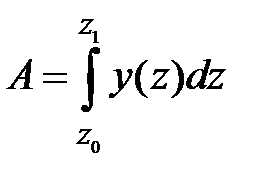
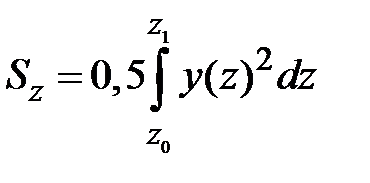
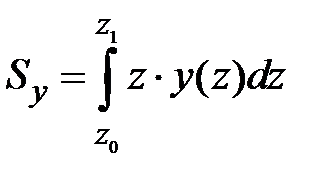
(1.12)

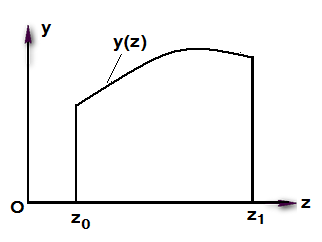
Рис. 1.11 Плоская фигура, ограниченная кривой 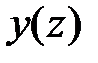на

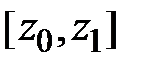
Приведем аналогичные формулы для осевых и центробежного моментов инерции:

,

,

.

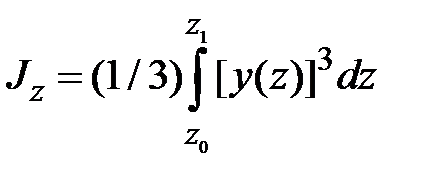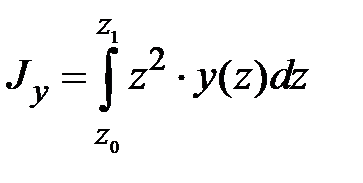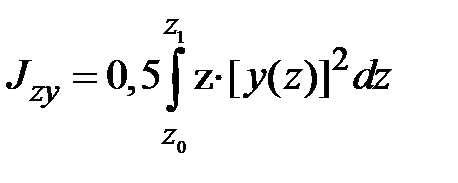(1.13)

Представим вывод формул (1.13).

Разобьем криволинейную трапецию на 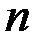частичных трапеций с помощью прямых, параллельных оси ординат, пересекающих ось абсцисс в точках 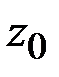, , 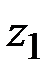,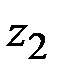…, , 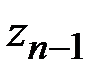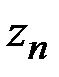(рис.1.12). Заменим каждую частичную трапецию прямоугольником, высотой которого является значение функции 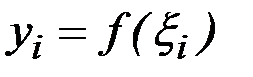в средней точке 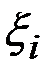частичного интервала: 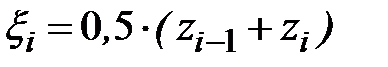, а основание 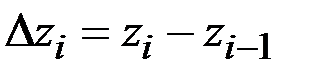. Центр тяжести каждого построенного прямоугольника известен: он расположен в точке .

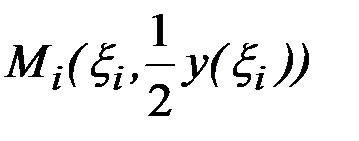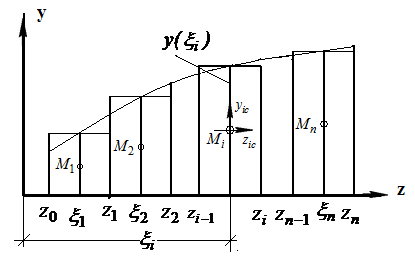
Рис. 1.12 К выводу формул (1.13)

1) Момент инерции прямоугольника относительно собственной центральной оси 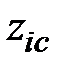равен (см.(1.11)): . Момент инерции прямоугольника относительно оси 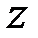, параллельной центральной (см. (1.8)):

.

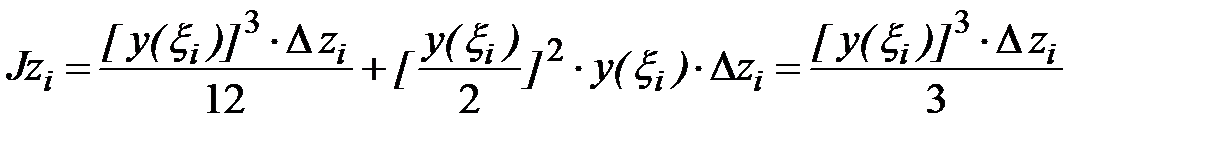Момент инерции 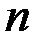прямоугольников определяем как сумму 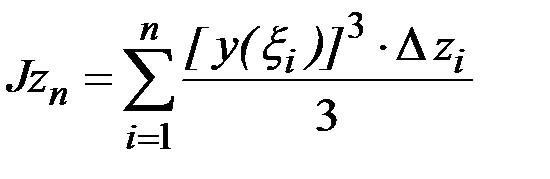. Устремляем 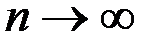и все 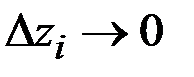, 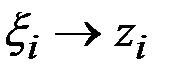. Пределом интегральной суммы будет интеграл .

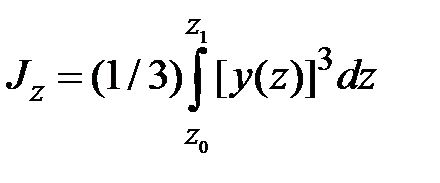2) Момент инерции прямоугольника относительно собственной центральной оси 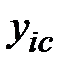, равен (вторая формула (1.11)): 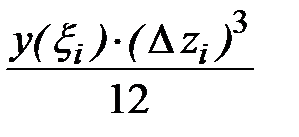. Момент инерции прямоугольника относительно оси 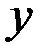(см. (1.8)) равен 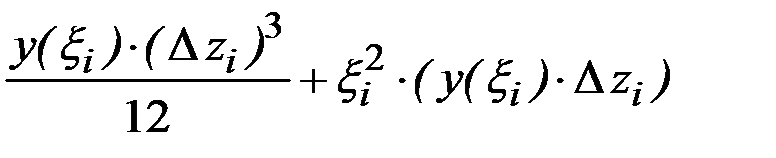. Момент инерции 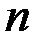прямоугольников определяем как сумму 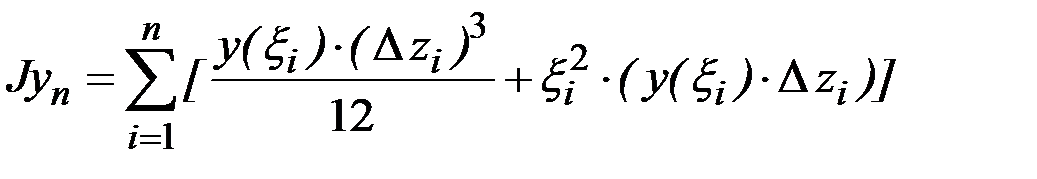. Устремляем 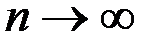и все 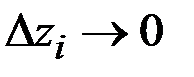, 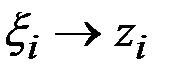. Слагаемые 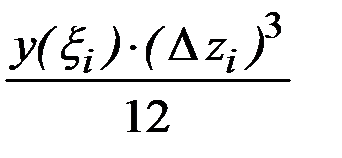имеют третий порядок малости относительно 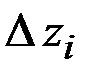, и поэтому ими можно пренебречь. Пределом интегральной суммы будет интеграл .

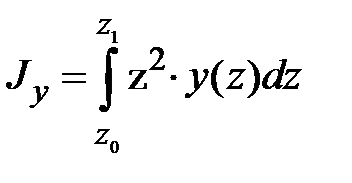Центробежный момент инерции прямоугольника относительно центральных осей равен нулю (третья формула (1.11)) . Центробежный момент инерции прямоугольника относительно осей 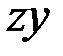, параллельных центральным осям равен 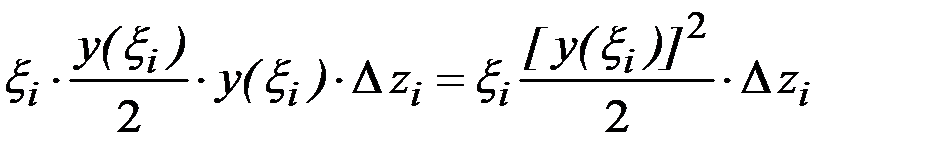. Центробежный момент инерции 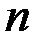прямоугольников определяем как сумму 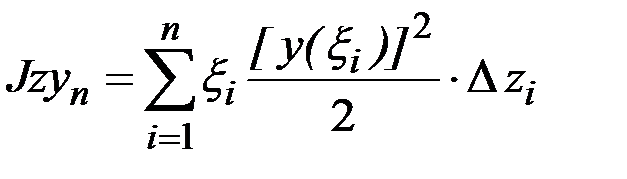Устремляем 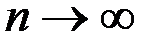и все 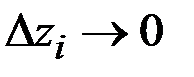, 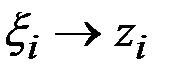Пределом интегральной суммы будет интеграл .

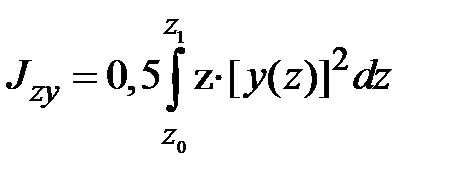Пример 1.3 Найдем координаты центра тяжести прямоугольного треугольника 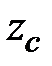, 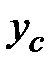(рис.1.13), осевые и центробежный моменты инерции.

Используем формулы (1.12) для 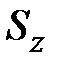и .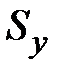

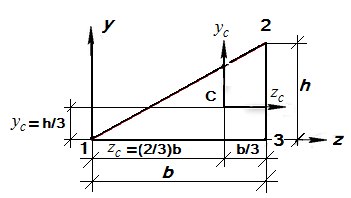
Рис.1.13Прямоугольный треугольник

Уравнение прямой 1-2: 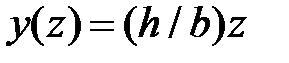. Отрезок интегрирования 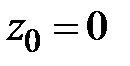, 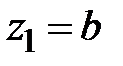. Площадь 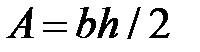. Статические моменты .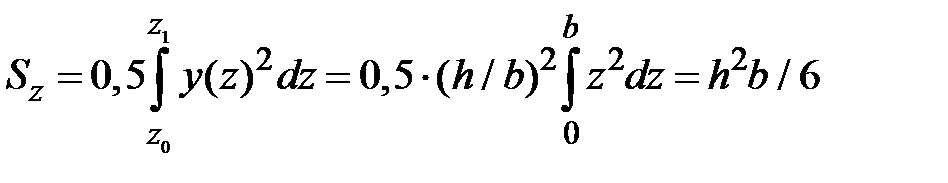

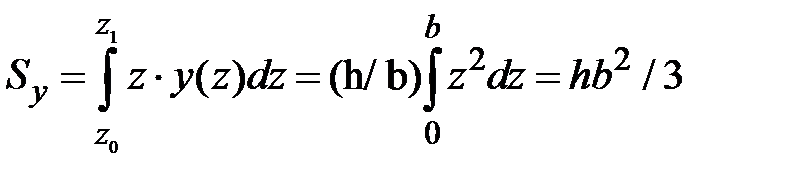Координаты центра тяжести: ; .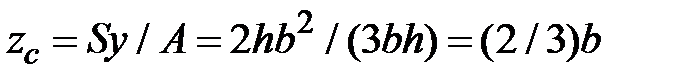

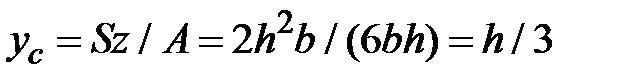Таким образом, центр тяжести в прямоугольном треугольнике удален от вершины прямого угла на 1/3 длин катетов.

Из курса аналитической геометрии известно, что координаты центра тяжести произвольного треугольника определяются через координаты вершин треугольника по формулам:

,

.

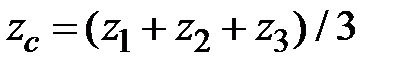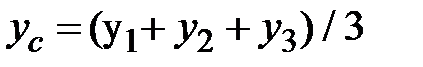(1.14)

Например, для треугольника (рис.1.13) получим:

; .

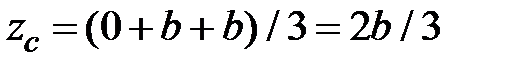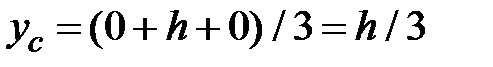Определим центробежный момент инерции прямоугольного треугольника относительно центральных осей 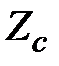, 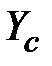(рис.1.13).

Сначала определим 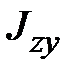, а затем с помощью формул (1.13) найдем 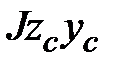. Воспользуемся формулой (1.13). В данном случае уравнение прямой 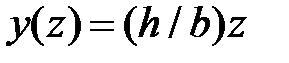. Отрезок интегрирования 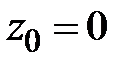, 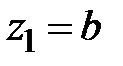. Площадь . .

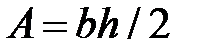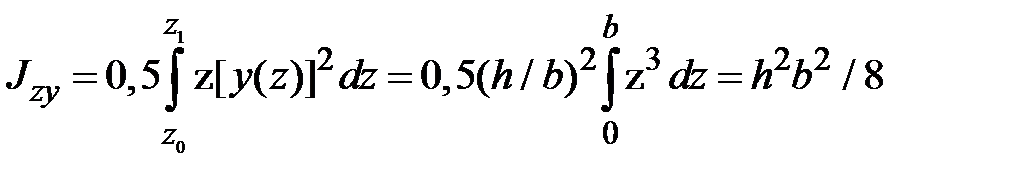Из формулы (1.8) имеем

.

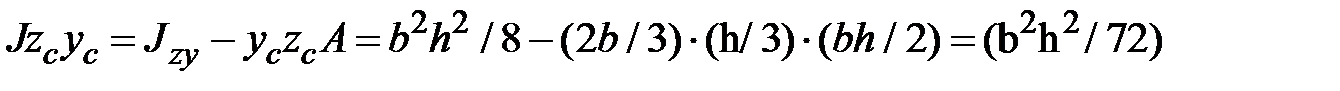Осевые моменты инерции :

;

;

;

.

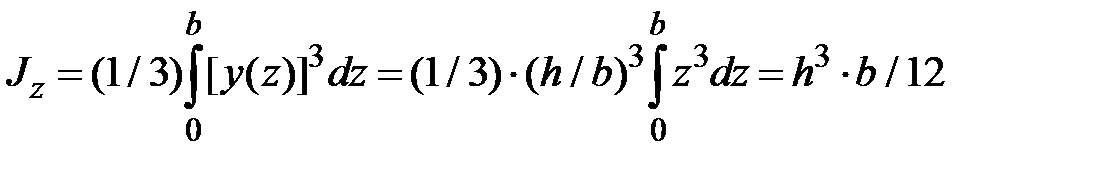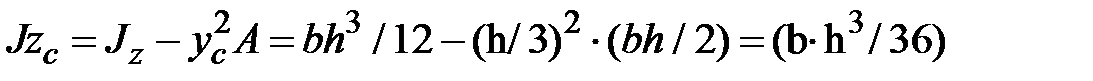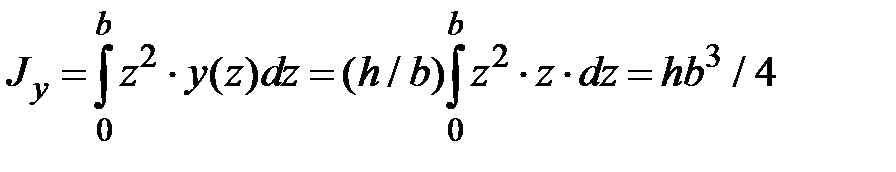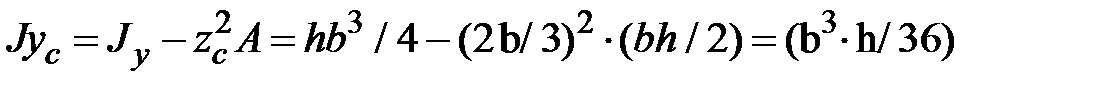Пример 1.4 Найдем координату центра тяжести полукруга 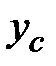(рис.1.14). Используем формулу (1.12) для .

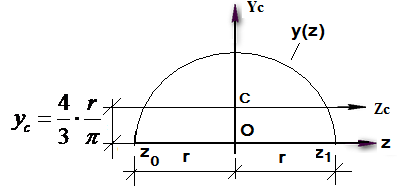
Рис.1.14 Полукруг

Уравнение дуги полуокружности 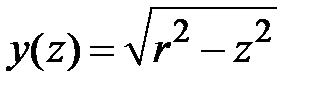, , 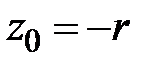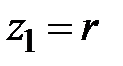. Статический момент равен

,

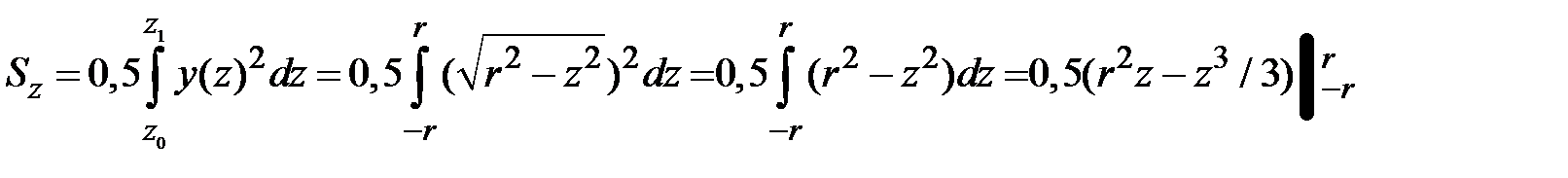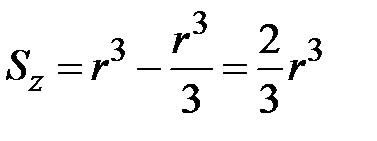. Следовательно, .

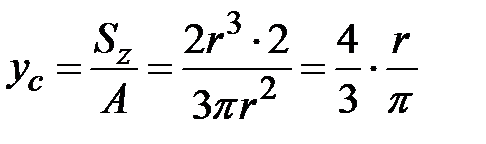Момент инерции относительно оси

.

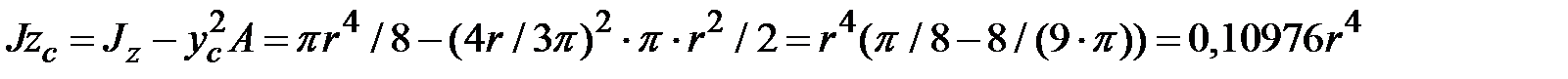
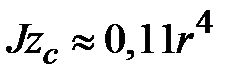Пример 1.5Определить центробежный момент инерции для четверти круга.

Определим сначала центробежный момент инерции 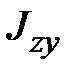для четверти круга (рис.1.15). Воспользуемся формулой (1.13). В данном случае уравнение 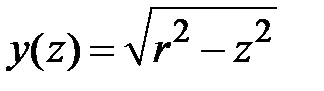. Отрезок интегрирования , .

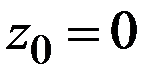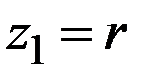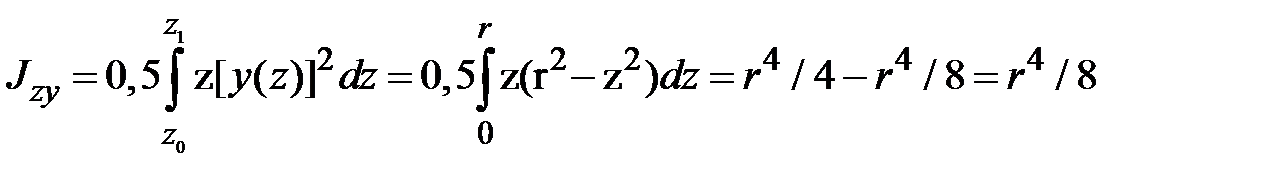
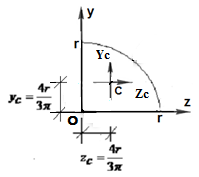
Рис. 1.15 К определению моментов инерции четверти круга

.

Относительно центральной оси

.

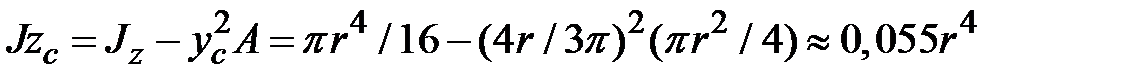Центробежный момент инерции относительно центральных осей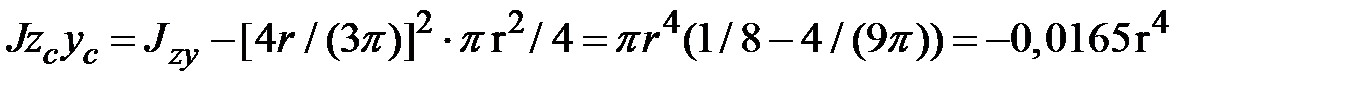

В табл. 1 представлены значения осевых и центробежного моментов инерции для простых фигур относительно собственных центральных осей.

Геометрические характеристики прокатных профилей приведены в приложении 1.