Новый энергетический параметр стабильности кристаллического вещества - энергия сцепления атомных остовов и связующих электронов

До недавнего времени были известны два энергетических подхода к кристаллическому веществу: 1) основанный на концепции энергии кристаллической ионной решетки (энергии разрыва кристалла на свободные составляющие ионы) и 2) основанный на концепции энергии атомизации (энергии разрыва кристалла на свободные нейтральные составляющие атомы).

Следует признать, что по сравнению с ведущим вторым подходом первый энергетический подход имеет менее универсальный характер и соответственно ограниченные возможности в смысле предсказания физических свойств разнообразных кристаллических соединений и, в частности, металлов. Поэтому некоторые современные ученые не только предают забвению первый энергетический подход, но и фактически предлагают от него отказаться, как от устаревшего и неудовлетворительного. Хотя мы и не вполне разделяем эту точку зрения, однако в указанной ситуации разработка (предложение) еще одного принципиально нового конкурентноспособного энергетического подхода к кристаллам (и оценке их разнообразных физических свойств) представляется вполне оправданной, актуальной и целесообразной.

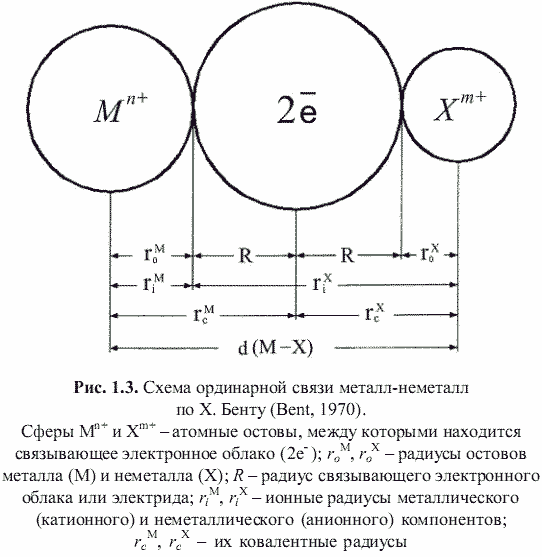
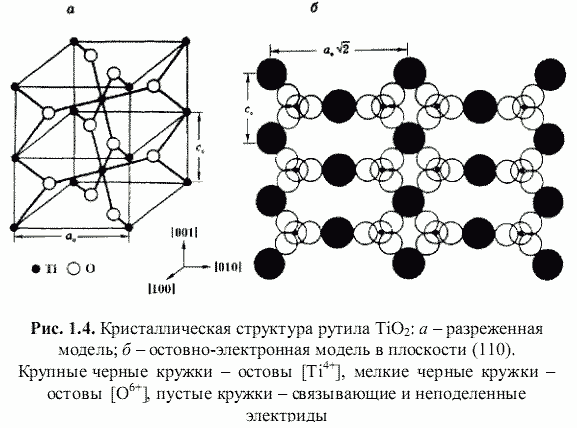
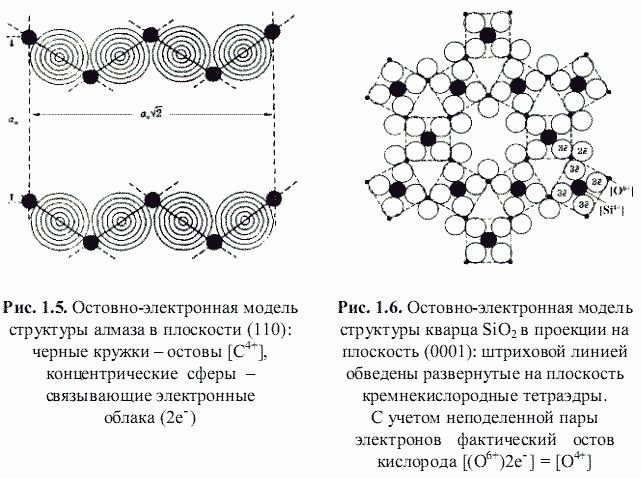
Как оказалось, теоретически возможен также третий энергетический подход к кристаллам, основанный на остовно-электронном моделировании их строения (Зуев, 1990). Напомним, что остовно-электронная концепция рассматривает кристаллическое соединение, независимо от типа химической связи, состоящим из положительно заряженных атомных остовов[1] (как металла, так и неметалла) и связывающих или поделенных (а также несвязывающих или неподеленных) валентных электронов. Принимая для тех и других, согласно (Bent, 1970; Зуев, 1990), сферическую форму (рис. 1.3), были построены соответствующие остовно-электронные модели кристаллических структур минералов, примеры которых приведены на рис. 1.4-1.8. Связывающие электронные облака можно именовать электридами, а соответствующие модели - остовно-электридными. Таким путем удается описать (хотя и с известной долей упрощения) строение соединений всех без исключения классов - будь то металлы, ковалентные или ионные кристаллы.[2]

Естественно предположить, что основу сцепления положительных остовов и отрицательных электридов в моделях типа изображенных на рис. 1.4-1.8 будет составлять электростатическое взаимодействие, энергию которого можно рассчитать в рамках концепции кристаллической ионной решетки, в которой атомные остовы являются катионами, а электриды - анионами. И, как нам представляется, наряду с энергией классической ионной решетки и энергией атомизации (используемых в первом и втором энергетических подходах), энергия остовно-электронного взаимодействия кристаллов в рамках третьего энергетического подхода может служить объективной мерой их стабильности и использоваться для оценки их свойств подобно тому, как это показано в работах (Зуев, Мочалов, Щербатов, 1998; Зуев, Аксенова, Мочалов и др., 1999). Схематически различие трех указанных энергетических подходов лучше всего продемонстрировать на конкретном примере обладающего тетраэдрической координацией атомов кристалла ZnS (сфалерита):

1. ZnS → Zn²⁺ + S^2- + U;

2. ZnS → Zn⁰ + S⁰ + E_а;

3. ZnS → Zn²⁺ + S⁶⁺ + 8e^- + W,

где выражаемые в кДж/моль или МДж/моль соответственно: U - энергия кристаллической решетки, Е_а - энергия атомизации (энергия сцепления атомов), W - энергия сцепления двух остовов (Zn²⁺, S⁶⁺) и четырех двухзарядных электридов (4x2e^-).

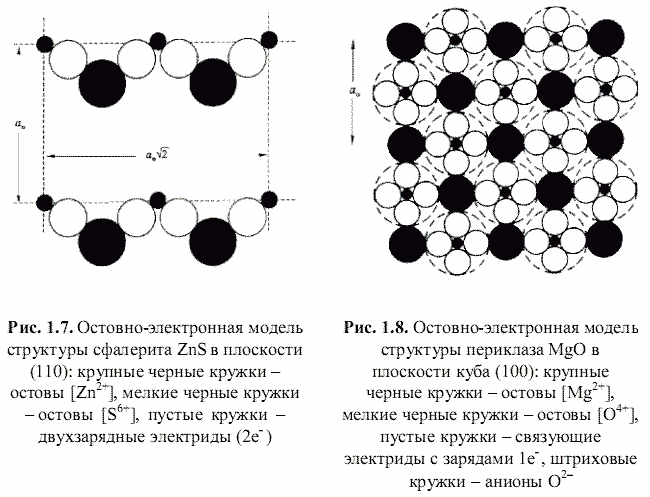
Соответствующая остовно-электронная модель для сфалерита, согласно рис. 1.7, -|[Zn²⁺](2e^-)₄[S⁶⁺]| т. е. на формульную единицу сфалерита приходится шесть заряженных частиц (два остова и четыре электрида). Остовно-электронная модель периклаза (рис. 1.8) - |[Mg²⁺](1e^-)₆[O⁴⁺]| - содержит два остова и шесть электридов (восемь частиц). Важно подчеркнуть, что если координационное окружение остовов электридами соответствует координационным числам (КЧ) атомов соединения, то для всех электридов имеет место линейная координация остовами (КЧ = 2).

В результате уточнения и дополнения классической формулы ионной кристаллической решетки (Урусов, 1975, с. 23; Харрисон, 1983, с. 22), нами была выведена следующая формула энергии сцепления остовов и электридов для общего случая кристаллического соединения[3]:

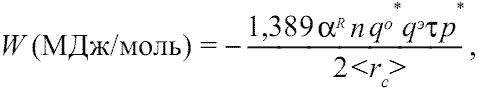(1.9)

где: 1,389 - константа для выражения энергии сцепления остовов и электридов в МДж/моль[4]; α_R - приведенная (связевая) константа Маделунга; n - суммарное число остовов и электридов, приходящихся на формульную единицу соединения; q_o* - суммарный эффективный заряд ядра, действующий на валентные (сверх остовные) электроны атома; q_э - заряд электрида; τ - коэффициент отталкивания, равный 0,1¸0,7; p* - коэффициент, характеризующий ковалентность связей, равный (1-f_i²)^1/2, где f_i - ионность соединения[5]; 2<r_c>, (Å) - удвоенное среднее межатомное расстояние остов-электрид, равное удвоенным усредненным величинам ковалентных радиусов образующих кристалл атомов. Напомним, что в остовно-электронной модели ковалентный радиус атома равен сумме соответствующих ионных радиусов остова и электрида. Таким образом, для соединений МxXy, согласно схеме на рис. 1.3, можно записать: 2<r_c^M,X> = 2(r_c^M + r_c^X)/2 =
= r_cM + r_cX = d(M-X), где d -межатомное расстояние металл - неметалл в структуре. Следовательно, в знаменателе формулы (1.9) вместо члена 2<r_c> можно поместить параметр d, Å среднего межатомного расстояния металл - неметалл соответствующего соединения:

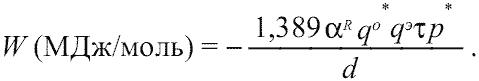(1.10)

Очевидно, что в случае сложных кристаллических соединений в расчетах по формуле (1.10) необходимо использовать усредненные параметры q_o*, q_э, f_i, d.

Как указывалось, вместо номинального заряда остова (например, Na⁺, Zn²⁺, Al³⁺, C⁴⁺, S⁶⁺ и т. д.) в формуле (1.10) используется, согласно (Зуев, 1990; Зуев, Денисов, Мочалов и др., 2000), более адекватно характеризующий силовое поле остова параметр:

q_o* = ΣZ_i*, (1.11)

где Z_i* - эффективные заряды ядра, действующие на валентные электроны и рассчитываемые по формуле (Zhang, 1982):

Z* = n*(I_w/R)^1/2, (1.12)

где n* - эффективное главное квантовое число, I_w (эВ) - потенциал ионизации атома соответствующей валентности (w), R - потенциал ионизации атома водорода, равный 13,595 эВ.

Например, расчеты по этим формулам дают для остовов:

[Na⁺] - q_o* = 2,89(5,138/13,595)^1/2 = 1,78;

[Zn²⁺] - q_o* = 3,45(9,391/13,595)^1/2 + 3,45(17,96/13,595)^1/2 = 6,83;

[C⁴⁺] - q_o* = 1,99(11,264/13,595)^1/2 + 1,99(24,376/13,595)^1/2 +

+1,99(47,86/13,595)^1/2 + 1,99(64,48/13,595)^1/2 = 12,54;

[S⁶⁺] - q_o* = 2,89(10,357/13,595)^1/2 + 2,89(23,4/13,595)^1/2 +

+ 2,89(34,8/13,595)^1/2 + 2,89(47,29/13,595)^1/2 +

+ 2,89(72,5/13,595)^1/2 + 2,89(88/13,595)^1/2 = 30,35 и т. д.

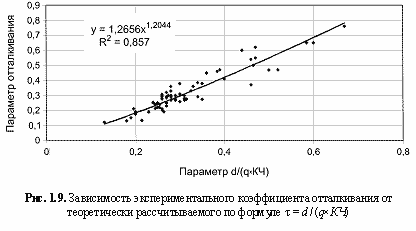
Необходимо объяснить сравнительно малую величину (0,1-0,7) коэффициента отталкивания, который в случае ионных кристаллических решеток гораздо выше (около 0,9). С одной стороны, это связано со значительным ростом положительных зарядов q_o* по сравнению с соответствующими номинальными. С другой стороны, остовно-электронные модели кристаллов являются по образному выражению Бента (Bent, 1970) постройками из «ионов внутри ионов», что наглядно показано на примере периклаза на рис. 1.8. Этими обстоятельствами и объясняется столь сильное взаимное отталкивание одноименно заряженных частиц в остовно-электридных моделях. Обычно параметр t находится из данных по сжимаемости кристаллов. Нами для его оценки была выведена (рис. 1.9) следующая эмпирическая формула:

τ = 1,2656[d/(qxКЧ)]^1.2, (1.13)

где d - межатомное расстояние в структуре; q - заряд электрида; КЧ - координационное число атомов (для сложных кристаллов все эти параметры являются средними для рассматриваемой структуры величи­нами).

Следует специально остановиться на оценке константы Маделунга α_R, строгий вывод которой для сложных остовно-электронных моделей структур весьма трудоемок. Поэтому нами принят упрощенный метод ее расчета по формуле Темплтона (Урусов, 1975):

α_R = 1,89 - 1/n x Σn_i/КЧ_i. (1.14)

Здесь n_i - число частиц (остовов, электридов) i-сорта с соответствующими координационными числами; n - общее число остовов и электридов, приходящихся на формульную единицу соединения.

Например, для имеющего в своем составе два остова и четыре электрида сфалерита ZnS расчет по формуле (1.14) приводит к
α_R = 1,89 - (2/4 + 4/2)/6 = 1,473. Для периклаза MgO (с двумя остовами и шестью электридами) получается такая же величина α_R = 1,89 - (2/6 + 6/2)/8 = 1,473. Если (см. рис. 1.6) неподеленную пару электронов включить в остов атома кислорода, то остовно-электронная модель кварца будет |[Si4+](3e-)₄[O4+]₂|, и в этом случае α_R = 1,89 - (1/4 + 2/2 + 4/2)/7 = 1,426.

Остановимся также подробнее на физическом смысле параметра р* в формуле (1.10). С этой целью рассмотрим ряд изоэлектронных и изоструктурных (типа сфалерита) соединений GeGe, GaAs, ZnSe, CuBr (таблица 1.10). Если обратиться к остовно-электронным схемам отдельных межатомных связей: [Ge⁴⁺](2e^-)[Ge⁴⁺], [Ga³⁺](2e^-)[As⁵⁺], [Zn²⁺](2e^-)[Se⁶⁺] и [Cu¹⁺](2e^-)[Br⁷⁺] этих соединений, то они оказываются практически идентичными по всем кристаллохимическим параметрам (средним зарядам остовов, зарядам электридов, межатомным расстояниям и др.), по величинам энергий гипотетических неполярных (λ = 0) ковалентных связей, а также по величинам формульных весов, мольных объемов и плотностей. Тем не менее, в ряду CuBr→ZnSe→GaAs→GeGe имеет место явно ощутимый, закономерный рост термодинамической и механической стабильности соединений (фиксируемый соответствующим увеличением их энергоплотности E_v и относительной твердости Н_М).

Таблица 1.10