Коэффициенты гармонической линеаризации типовых нелинейностей

Статическая характеристика нелинейного элемента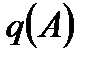
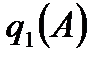
Линейная характеристика с зоной нечувствительности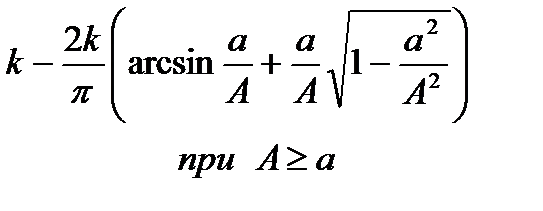
Линейная характеристика с ограничением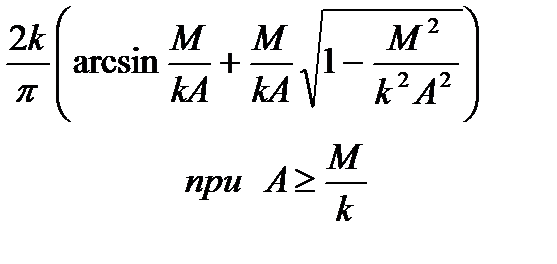
Линейная характеристика с зоной нечувствительности и ограничением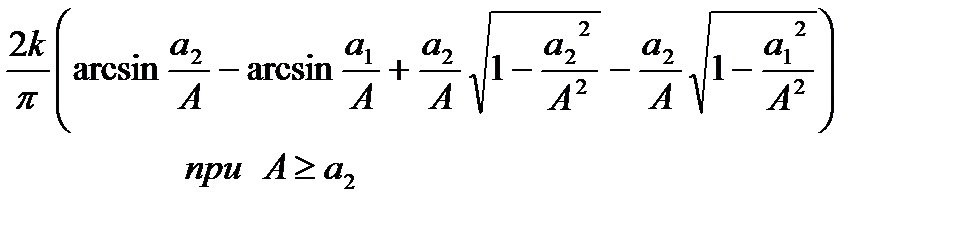
Характеристика «люфт»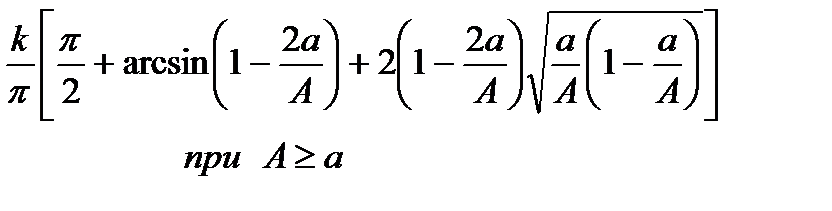
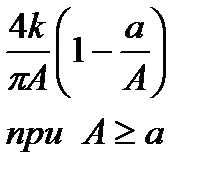
Идеальная релейная характеристика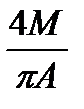
Однозначная релейная характеристика с зоной нечувствительности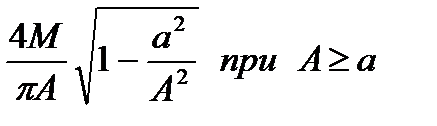
Неоднозначная релейная характеристика с зоной нечувствительности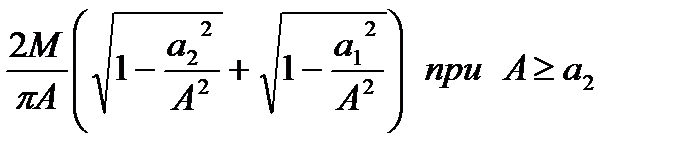
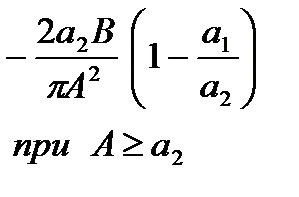
Кубическая парабола: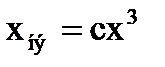
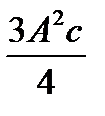
Характеристика «петля гистерезиса»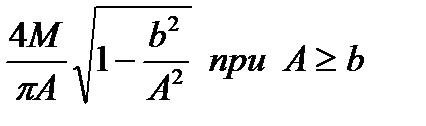

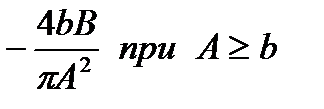
Передаточная функция 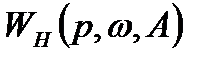нелинейного эле­мента имеет существенное отличие от передаточной функ­ции линейной системы 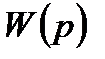, заключающееся в том, что 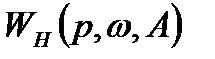зависит от амплитуды и частоты входного сигнала.

Выражение (8.22) запишем в виде:

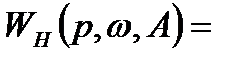q(A) + 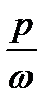q₁(A), (8.23)

где q(A), q₁(A) – коэффициенты гармонической линеаризации, определяемые как отношения коэффициентов ряда Фурье для пер­вой гармоники выходных колебаний к амплитуде вход­ных колебаний:

q(A) = 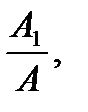q₁(A) = 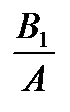. (8.24)

Заменяя в выражении (8.23) р на 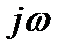, получим выражение для комплексного коэффициента передачи нелинейного элемента:

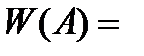q(A) +j q₁(A), (8.25)

являющегося аналогом АФХ для линейного звена.

В качестве примера определим выражение для комплексного коэффициента передачи нелинейного элемента с релейной статической характеристикой (8.14). Коэффициенты ряда Фурье A₁ и B₁ для указанной нелинейности равны:

;

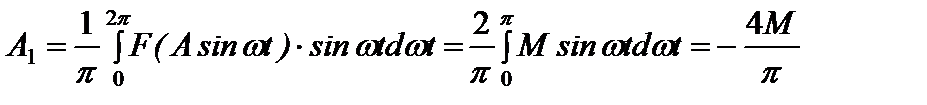B₁ .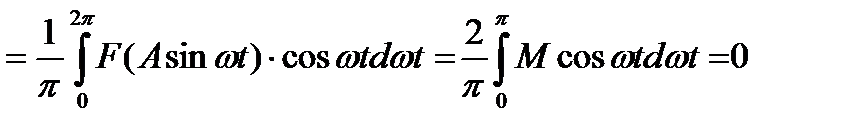

Очевидно, что коэффициент B₁ будет равен нулю для любого нелинейного элемента с нечетно-симметричной статической нелинейностью.

Тогда, согласно выражениям (8.24) и (8.25) получим:

q(A) = 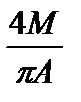; q₁(A) = 0 и W(A) = .

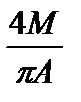Значения коэффициентов гармонической линеаризации для нескольких типовых нелинейностей приведены в таблице 8.1.