Методы определения параметров автоколебаний

Если в замкнутой нелинейной системе САУ возникают автоколебания с постоянной амплитудой и частотой, то коэффициенты гармонической линеаризации оказывают­ся постоянными, а вся система стационарной. Незатуха­ющие колебания в замкнутых системах возникают в том случае, когда характеристиче­ское уравнение системы содержит пару мнимых сопря­женных корней.

Характеристический полином замкнутой системы (рис.8.1) при осуществлении гармонической линеаризации входящего в нее нелинейного звена запишем в виде:

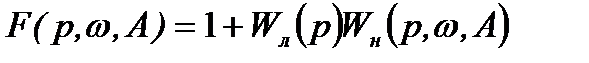, (8.26)

где 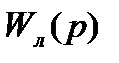—передаточная функция линейной части си­стемы; 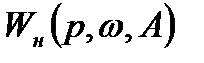—передаточная функция нелинейного элемента после его линеаризации.

Если 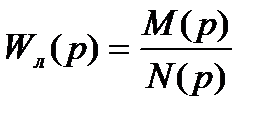, то выражение (8.26) можно записать в виде:

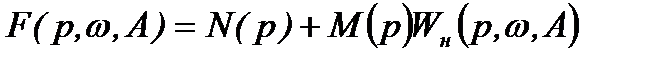. (8.27)

Заменяя в выражении (8.27) р на 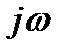, по­лучим комплексное выражение, в котором необходимо выделить вещественную 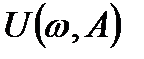и мнимую 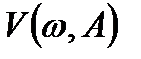части:

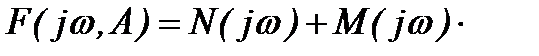[ q(A) +j q₁(A)] 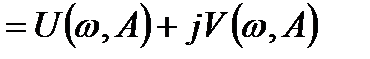. (8.28)

При этом условие возникновения периодических колебаний в системе с частотой 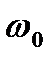и амплитудой 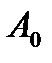запишем:

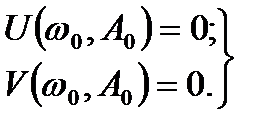(8.29)

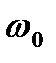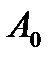Если решения системы (8.29) комплексные или отрицательные, режим автоколебаний в системе невозможен. Наличие положительных вещественных решений для и свидетельствует о наличии в системе автоколебаний, которые необходимо проверить на устойчивость.

В качестве примера найдем условия возникновения автоколеба­ний в САУ, если передаточная функция ее линейной части равна:

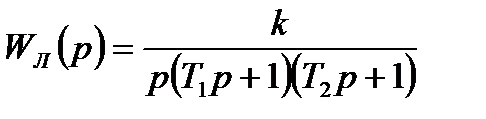(8.30)

и нелинейным элементом типа «петля гистерезиса».

Передаточная функция гармонически линеаризованного нелинейного элемента (см. табл. 8.1) имеет вид:

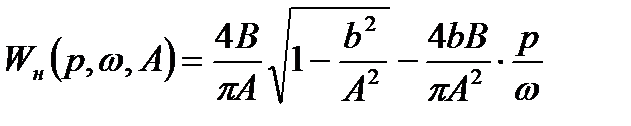. (8.31)

Подставляя выражения (8.30) и (8.31) в выражение (8.26) и заменяя р на 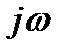, найдем выражение для :

.

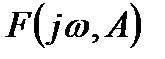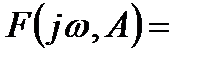
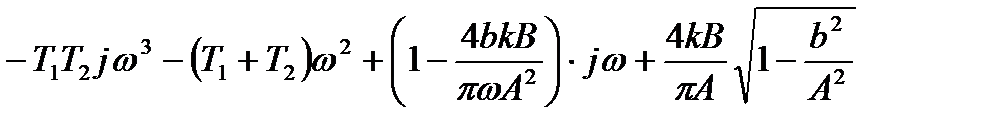Отсюда в соответствии с выражением (8.29) получаем следующие условия возникновения автоколебаний в системе:

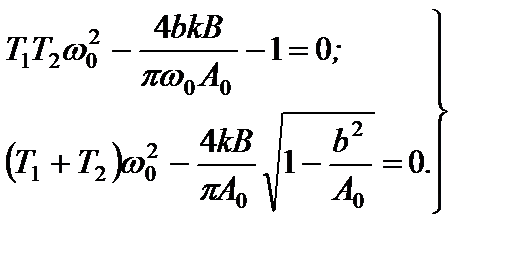
Решение системы уравнений (8.29) обычно затруднительно, так как ко­эффициенты гармонической линеаризации имеют слож­ную зависимость от амплитуды входного сигнала. Кроме того, помимо определения амплитуды 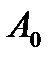и частоты 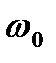, необходимо оценить устойчивость автоколебаний в системе.

Условия возникновения автоколебаний в нелинейной системе и параметры предельных циклов можно исследо­вать, используя частотные критерии устойчивости, например, критерий устойчи­вости Найквиста. Согласно этому критерию при наличии автоколебаний амплитудно-фазовая характеристика разомкнутой гармонически линеаризованной системы, равная

= ,

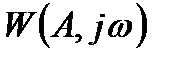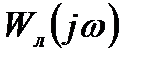
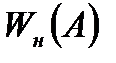проходит через точку (-1, j0). Следовательно, для 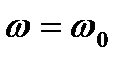и 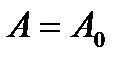справедливо равенство:

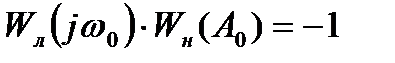
или

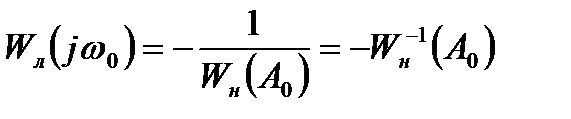. (8.32)

Решение уравнения (8.32) относительно частоты и амплитуды автоколебаний можно получить графически. Для этого на комплексной плоскости необходимо, изменяя частоту 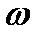от 0 до 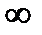, построить годограф АФХ линейной части системы 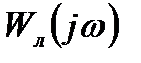и, изменяя амплитуду А от 0 до 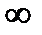, построить годограф обратной ха­рактеристики нелинейной части 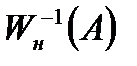, взятый с знаком «минус». Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует (рис. 8.18, б).

Рис. 8.18. К определению наличия и устойчивости автоколебаний в нелинейной системе

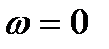
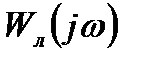
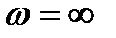
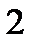
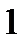
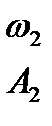
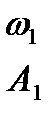
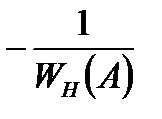
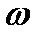
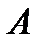
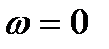
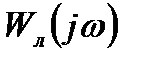
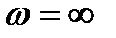
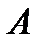
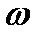
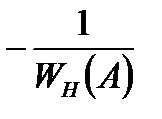
а)

б)

При пересечении годографов (рис. 8.18, а) в системе возникают автоколебания, частота и амплитуда которых опреде­ляются значениям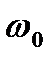и и 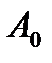в точке пересечения.

Есл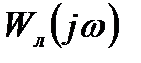и и - 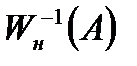пересекаются в нескольких точках (рис. 8.18, а), то это свидетельствует о наличии в системе нескольких предельных циклов. При этом колебания в системе могут быть устойчивы­ми и неустойчивыми.

Устойчивость автоколебательного режима оценивается следующим образом. Режим автоколебаний устойчив, если точка на годографе нелинейной части 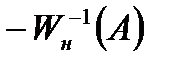, соответствующая амплитуде большей по сравнению со значением в точке пересечения годографов, не охватывается годографом частотной характеристики линейной части системы. В противном случае автоколебательный режим неустойчив.

На рис. 8.18, а годографы пересекаются в точках 1 и 2. Точка 1определяет неустойчивый режим автоколебаний, так как точка годографа 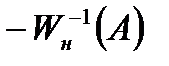, соответствующая увеличенной амплитуде, охватывается годографом частотной характеристики линейной части системы. Точке 2 соответствует устойчивый режим автоколебаний, амплитуда которых определяется по годографу 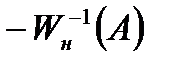а частота – по годографу .

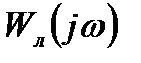В качестве примера оценим устойчивость автоколебаний в двух нелинейных системах. Будем полагать, что передаточные функции линейных частей этих систем совпадают и равны:

,

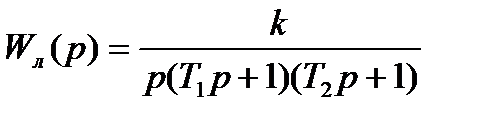но входящие в них их нелинейные элементы различны. Пусть в первую систему включен нелинейный элемент «идеальное реле», описываемый системой (8.14), а во вторую – нелинейный элемент со статической характеристикой «кубическая парабола». Воспользовавшись данными таблицы 8.1, получим:

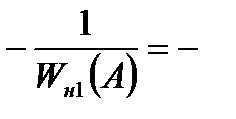
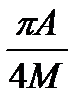и – .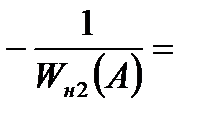

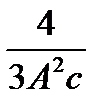Рис. 8.19. К оценке устойчивости автоколебаний

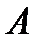
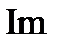
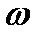
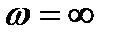
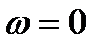
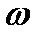
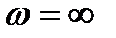
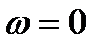
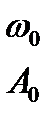
а)

б)

На рис. 8.19 изображены годографы 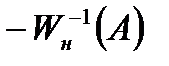этих систем совместно с годографом АФХ линейной части системы 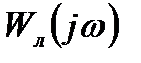. На основании изложенного можно утверждать, что в первой системе возникают устойчивые автоколебания с частотой 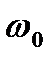и амплитудой 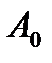, а во второй системе автоколебания неустойчивые.

Литература

1. Теория автоматического регулирования: Учеб. пособие/ А.С.Востриков, Г.А.Французова - М.: Высшая школа, 2004.- 365 с.

2. Пупков К.А., Егупов Н.Д., Баркин А.И. и др. Методы классической и современной теории автоматического управления. В 5 томах. Том 1. Математические модели, динамические характеристики и анализ систем автоматического управления. – М.: Издательство МГТУ им. Н. Э. Баумана, 2004 – 656 с.

3. Теория автоматического управления: Учебник для вузов/ С.Е. Душин,

Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В.Б.Яковлева.– М.: Высшая школа, 2003.– 567 с.

4. Мирошник И.В. Теория автоматического управления. Линейные системы. – СПб.: Питер, 2005. – 336 с.: ил.

5. Пупков К.А., Егупов Н.Д., Баркин А.И. и др. Методы классической и современной теории автоматического управления. В 5 томах. Том 2. Статистическая динамика и идентификация систем автоматического управления . – М.: Издательство МГТУ им. Н. Э. Баумана, 2004 – 656 с.

6. Мирошник И. В. Теория автоматического управления. Часть 2. Нелинейные и оптимальные системы. – СПб.: Питер, 2005. – 336 с.: ил.

7. Никулин Е. А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем. – СПб.: БХВ-Петербург, 2004. – 640 с.

8. Теория автоматического управления: Учебное пособие для ВУЗов/ Анхимюк В. Л., Опейко О. Ф., Михеев Н. Н. – М.: Дизайн ПРО, 2002. – 352 с.

9. Ерофеев А.А. Теория автоматического управления: Учебник для вузов Изд. 2-е, перераб., доп., 2001

10. Брюханов В.Н., Косов М.Г., Протопопов С.П. и др. Теория автоматического управления: Учебник для вузов (под ред. Соломенцева Ю.М.) Изд. 2-е, испр./ 3-е, 2001

11. Пупков К.А., Егупов Н.Д., Баркин А.И. и др. Методы классической и современной теории автоматического управления. В 5 томах. Том 3. Синтез регуляторов систем автоматического управления. – М.: Издательство МГТУ им. Н. Э. Баумана, 2004 – 656 с.

12. Воронов А.А. Основы теории автоматического управления: Особые линейные и нелинейные системы. – 2-е изд. перераб. и доп. – М.: Энергия, 1981. – 304 с.

13. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем: Учебник для вузов. – М.: Машиностроение, 1978. – 736 с.

14. Цыпкин Я.З. Основы теории автоматических систем. – М.: Наука, 1977. – 560 с.

15. Бессекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука, 2004. – 768 с.

16. Теория автоматического управления / Под ред. А.С. Шаталова. – М.: Высшая школа, 1977. – 448 с.

17. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. Учебное пособие для вузов. – М.: Машиностроение, 1985. – 536 с.

18. Сборник задач по теории автоматического регулирования / Под ред. В.А. Бессе­керского. – М.: Наука, 1972. – 588 с.

19. Задачник по теории автоматического управления / Под ред. А.С. Шаталова. – 2-е изд., перераб. и доп. – М.: Энергия, 1979. – 544 с.

20. Теория автоматического управления. Учебник для вузов/Под ред. В.Б.Яковлева.- М.: Высшая школа, 2003.-567 с.

21. Теория управления в примерах и задачах: Учебное пособие/ А.В.Пантелеев, А.С.Бортаковский.- М.: Высшая школа, 2003.-583 с.

22. Ю.В.Бородакий, Ю.Г.Лободинский. Основы теории систем управления. Исследование и проектирование – М.: Радио и связь, 2004. – 254 с.

23. http:// www.toehelp.ru/theory/tau/contents.html

24. http:// zdo.vstu.edu.ru/html/course.html

25. http:// www.ispu.ru/library/lessons/faleev/