Весовые коэффициенты важности критериев
В рамках решения многокритериальных задач имеют место дополнительные трудности, связанные с получением информации от ЛПР о значимости отдельных критериев. Естественное решение этой проблемы основано на агрегировании нескольких критериев в один с помощью весовых коэффициентов важности критериев. Комплексный критерий вычисляются по формуле
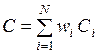 , (1)
, (1)
где 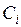 - частные критерии;
- частные критерии; 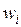 - веса (коэффициенты важности) критериев;
- веса (коэффициенты важности) критериев;
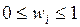 ,
, 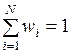 . (2)
. (2)
Идея такого объединения состоит в том, что ЛПР назначает числа (часто по численной шкале 1 - 100), представляющие для него ценность рассматриваемого критерия. Далее, весовые коэффициенты нормируются на основе условия (2). Обратимся к рисисунку 15. Легко увидеть, что решения, соответствующие точкам А и В на множестве Парето, могут быть представлены в виде
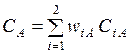 ,
, 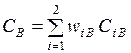
Существует лемма, утверждающая, что для линейной задачи любое эффективное, находящееся на множестве Э-П решение может быть предъявлено в виде (1). Следовательно, формально задача сводится к нахождению весов.
Возникла идея, оперативно получать эти веса от ЛПР. Если ЛПР затрудняется выбрать эти веси в начале процесса принятия решений (до изучения области допустимых значений D), то можно построить ЧМП следующего содержания. ЛПР назначает первоначальные веса, анализирует полученное решение и корректирует веса до получения удовлетворительного результата.
Классификация ЧМП
Известна классификация ЧМП, основанная на характере информации, получаемой от ЛПР на этапе анализа.
1. Прямые ЧМП - ЛПР непосредственно назначает веса критериев и корректирует их на основе полученных решений.
2. ЧМПоценки векторов - ЛПР сравнивает многокритериальные решения.
3. ЧМП поиска удовлетворительных решений - ЛПР выбирает ограничения на значения критериев и, следовательно, на область допустимых значений.
Проанализируем общие этапы предварительной обработки данных, встречающиеся вомногих ЧМП. Перед решением задачи рекомендуется нормировать критерии, преобразовав их к стандартному диапазону изменения от 0 до 1.
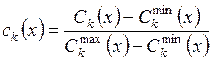
где 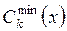 ,
, 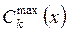 - минимальное и максимальное значения k- го критерия;
- минимальное и максимальное значения k- го критерия; 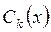 - текущее значение. Кроме того, как это было показано выше в примере раздела 7, для каждого из критериев вычисляется оптимальное абсолютное значение. Вектор таких совместно недостижимых значений помогает ЛПР оценить пределы фактически возможных величин.
- текущее значение. Кроме того, как это было показано выше в примере раздела 7, для каждого из критериев вычисляется оптимальное абсолютное значение. Вектор таких совместно недостижимых значений помогает ЛПР оценить пределы фактически возможных величин.
Дата добавления: 2017-09-01; просмотров: 3516;











