Реальные газы. Уравнение Ван-дер-Ваальса
Газовые законы, рассмотренные в предыдущих разделах, точно выполняются только для идеальных газов, которые не конденсируются при охлаждении их вплоть до абсолютного нуля температуры.
Свойства большинства газов близки к свойствам идеального газа, когда они находятся при температурах, достаточно далеких от точки конденсации, т.е. когда между молекулами отсутствует взаимодействие и когда собственный объем молекул газа мал по сравнению с объемом газа.
Вблизи точки конденсации (при высоком давлении и низкой температуре) свойство газов значительно отличается от свойств идеального газа. В этих случаях говорят о реальных газах.
Уравнение состояния для 1-го моля идеального газа 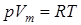 (Vm – молярный объем) видоизменяется в случае реальных газов.
(Vm – молярный объем) видоизменяется в случае реальных газов.
Для реальных газов необходим учет собственного объема молекул.
Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm , а Vm – b, b – объем, занимаемый самими молекулами. Объем b равен учетверенному собственному объему молекул.
Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т.е.
 ,
,
где a — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения.
Вводя поправки в уравнение 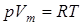 для идеального газа, получим уравнение Ван-дер-Ваальса для 1-го моля газа
для идеального газа, получим уравнение Ван-дер-Ваальса для 1-го моля газа
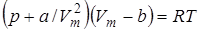 . (9.45)
. (9.45)
Учитывая, что 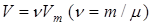 , получим уравнение для произвольного количества вещества:
, получим уравнение для произвольного количества вещества:
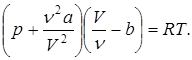 (9.46)
(9.46)
Поправки Ван-дер-Ваальса (a и b) являются постоянными для каждого газа величинами. Для их определения записывают уравнения для двух известных из опыта состояний газа и решаются относительно a и b.
Уравнение (9.45) можно записать в виде
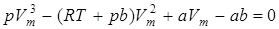 .
.
При заданных p и T — это уравнение третьей степени относительно Vm, следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни.
Изотермами Ван-дер-Ваальса называются кривые зависимости p от Vm при заданных T, определяемые уравнением Ван-дер-Ваальса для моля газа.
При некоторой температуре Tk — критической температуре— на изотерме (рис. 9.11.) только одна точка перегиба (в этой точке касательная к ней параллельна оси абсцисс). Точка K — критическая точка, соответствующие
 этой точке объем Vk и давление pk называются также критическими. Изотерма при Tk называется критической изотермой.
При высокой температуре (T>Tk) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При низкой температуре (T<Tk) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь. этой точке объем Vk и давление pk называются также критическими. Изотерма при Tk называется критической изотермой.
При высокой температуре (T>Tk) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При низкой температуре (T<Tk) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
|
Изотермам при низкой температуре (T<Tk) одному значению давления например, p1 соответствует три значения объема V1, V2 и V3, а при T>Tk — одно значение объема. В критической точке все три объема (три корня) совпадают и равны Vk.
Рассмотрим изотерму при T<Tk на рис. 9.12.
 | |||
 | |||
На участках 1–3 и 5–7 при уменьшении объема Vm давление p возрастает. На участке 3–5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3–5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма имеет вид ломанной линии 7–6–2–1. Часть 7–6 отвечает газообразному состоянию, а часть 2–1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6–2, наблюдается равновесие жидкой и газообразной фаз вещества.
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колокообразная кривая (рис. 9.13.), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму p, Vm под изотермой на три области: под колокообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа— область пара. Пар — вещество, находящееся в газообразном состоянии при температуре ниже критической. Насыщенный пар — пар, находящийся в равновесии со своей жидкостью.
Контрольные вопросы
1. Газ совершает над граничащими с ним телами отрицательную работу. Что происходит при этом с объемом газа?
2. Может ли случится, что газ получает теплоту, а его внутренняя энергия уменьшается?
3. Изменяется ли внутренняя энергия идеального газа при изотермическом расширении?
4. Всегда ли справедливо соотношение Cp-CV=R?
5. В ходе какого процесса работа, совершаемая телом, пропорциональна изменению его объема?
6. Чему равна работа, совершаемая в изохорическом процессе?
7. В ходе какого процесса работа, совершаемая телом, равна убыли его внутренней энергии?
8. Что такое вечный двигатель второго рода?
9. Может ли энтропия убывать в ходе необратимого процесса?
10. Какие величины, которыми пренебрегают, рассматривая идеальные газы, учитывает уравнение Ван-дер-Ваальса?
Дата добавления: 2016-06-05; просмотров: 3052;











