Применение первого начала термодинамики к изопроцессам
Изопроцессы — это равновесные процессы, в которых один из основных параметров сохраняется постоянным.
Изобарный процесс— это процесс, протекающий при постоянном давлении (p= const).
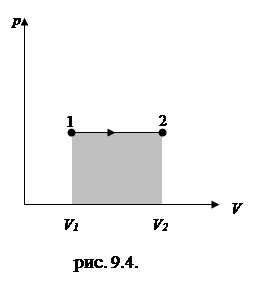
| Диаграмма этого процесса (изобара) в координатах p, V изображается прямой, параллельной оси V (рис. 9.4.). При изобарном процессе работа газа при увеличении объема от V1 до V2
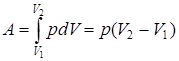 (9.15)
и определяется площадью закрашенного прямоугольника. Используя уравнение Клапейрона (9.15)
и определяется площадью закрашенного прямоугольника. Используя уравнение Клапейрона 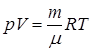 , получаем , получаем
|
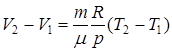 . (9.16)
. (9.16)
Поэтому работа изобарного расширения
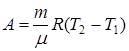 . (9.17)
. (9.17)
В изобарном процессе при сообщении газу массой m количества теплоты
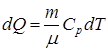 (9.18)
(9.18)
его внутренняя энергия возрастает на величину
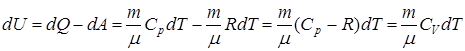 . Итак,
. Итак,
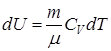 . (9.19)
. (9.19)
Изохорный процесс— это процесс, протекающий при постоянном объеме
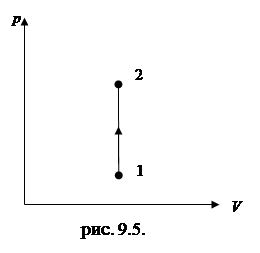
(V=const). Диаграмма этого процесса (изохора) в координатах p, V изображается прямой, параллельной оси ординат (на рис. 9.5.процесс 1-2 — изохорное нагревание). В изохорном процессе газ над внешними телами работы не совершает:
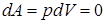 . (9.20)
. (9.20)
| Из первого начала терм одинамики 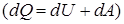 для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: 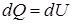 .
Согласно формуле (9.9) .
Согласно формуле (9.9) 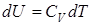 . Тогда для произвольной массы газа . Тогда для произвольной массы газа
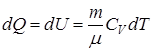 . (9.21) . (9.21)
|
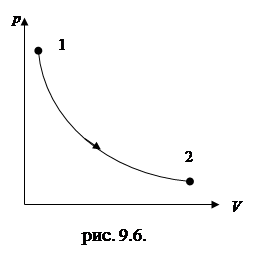
Изотермический процесс— это процесс, протекающий при постоянной температуре (T = const). Диаграмма этого процесса (изотерма) в координатах p, V изображается гиперболой (pV=const), (рис.9.5.). Учитывая, что 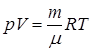 , работа изотермического расширения газа есть:
, работа изотермического расширения газа есть:
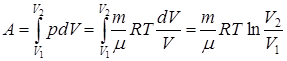 . (9.22)
. (9.22)
| Из первого начала термодинамики 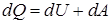 следует, что в изотермическом процессе следует, что в изотермическом процессе 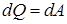 , т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: , т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
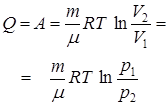 (9.23) (9.23)
|
Чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
Адиабатный процесс—это такой процесс, при котором отсутствуеттеплообмен между системой и окружающей средой (dQ = 0).
Из первого начала термодинамики 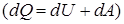 для адиабатического процесса следует, что
для адиабатического процесса следует, что 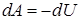 , т.е. внешняя работа совершается за счет изменения внутренней энергии системы. Перепишем это уравнение с учетом того, что
, т.е. внешняя работа совершается за счет изменения внутренней энергии системы. Перепишем это уравнение с учетом того, что 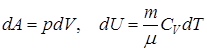 :
:
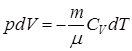 . (9.24)
. (9.24)
Возьмем полный дифференциал от левой и правой частей уравнения 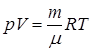 :
:
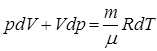 . (9.25)
. (9.25)
Разделив уравнение (9.25) на (9.24) и учитывая, что 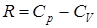 и
и 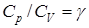 , найдем
, найдем
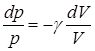 . (9.26)
. (9.26)
Интегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, а затем потенциируя, придем к выражению
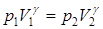 . (9.27)
. (9.27)
Состояния ( 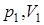 ) и (
) и ( 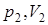 ) произвольны, поэтому искомое уравнение:
) произвольны, поэтому искомое уравнение:
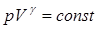 . (9.28)
. (9.28)
Уравнение (9.28) называется уравнением Пуассона.
Используя уравнение Клапейрона-Менделеева 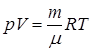 , можно из уравнения Пуассона найти связь между p и T, а также V и T в адиабатическом процессе:
, можно из уравнения Пуассона найти связь между p и T, а также V и T в адиабатическом процессе:
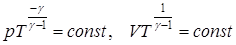 . (9.29)
. (9.29)
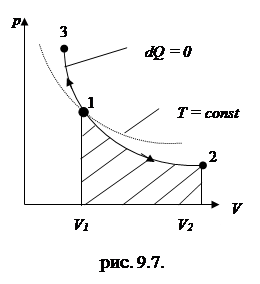
| Диаграмма адиабатного процесса (адиабата) в координатах p, V изображается гиперболой, правда, более крутой, чем изотерма (см. рис 9.7.). Это объясняется тем, что при адиабатном сжатии 1-3 увеличение p обусловлено не только уменьшением V (как при изотермическом процессе), но и повышением Т. Вычислим работу газа в адиабатном процессе. Из равенств 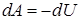 , , 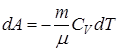 , получим , получим
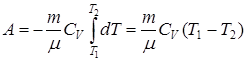 . (9.30) . (9.30)
|
Работа адиабатного расширения 1–2 (на рис. 9.6. определяется заштрихованной площадью) меньше, чем в изотермическом процессе. При адиабатном расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
В таблице 9.1 приведены сводные данные о характеристиках изопроцессов в газах.
Дата добавления: 2016-06-05; просмотров: 3439;











