Дрейф заряженной частицы, вызванный неоднородностью величины магнитной индукции.
 Допустим, что индукция магнитного поля
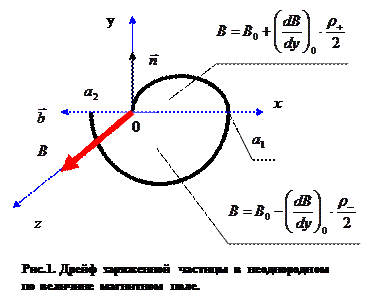
Допустим, что индукция магнитного поля 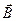 направлена вдоль оси z, магнитное поле практически не изменяет своего направления, величина его индукции медленно возрастает с координатой у как показано на рис. 1. Здесь
направлена вдоль оси z, магнитное поле практически не изменяет своего направления, величина его индукции медленно возрастает с координатой у как показано на рис. 1. Здесь 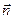 - направление главной нормали к силовой линии магнитной индукции,
- направление главной нормали к силовой линии магнитной индукции, 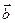 - направление бинормали к силовой линии магнитной индукции, т.е. направления осей координат выбрано специфическим образом. Поперечная скорость условно положительно заряженной частицы
- направление бинормали к силовой линии магнитной индукции, т.е. направления осей координат выбрано специфическим образом. Поперечная скорость условно положительно заряженной частицы 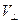 определяет вместе с величиной В ларморовский радиус траектории «быстрого движения». Определим его значение в верхней и нижней частях траектории выражением
определяет вместе с величиной В ларморовский радиус траектории «быстрого движения». Определим его значение в верхней и нижней частях траектории выражением
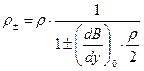 . (1)
. (1)
В этом случае положение точки а1 на оси х в конце движения по верхней части траектории оценивается величиной 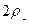 , а смещение влево по оси
, а смещение влево по оси 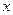 на нижней части траектории – величиной
на нижней части траектории – величиной 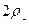 . В итоге частица за циклотронный период сместилась по оси
. В итоге частица за циклотронный период сместилась по оси 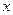 в положение с координатой
в положение с координатой 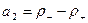 . Если разделить полученное выражение на циклотронный период, получим оценку дрейфовой скорости в рассматриваемом случае:
. Если разделить полученное выражение на циклотронный период, получим оценку дрейфовой скорости в рассматриваемом случае:
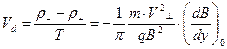 . (2)
. (2)
В более строгом анализе величина 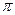 в этой формуле заменяется величиной 2, а зависимость для скорости дрейфа записывается в векторном виде:
в этой формуле заменяется величиной 2, а зависимость для скорости дрейфа записывается в векторном виде:
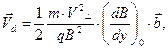 (3)
(3)
где 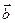 - орт направления бинормали к силовой линии магнитной индукции. Заметим, что соотношением (2) скорость дрейфа определена как проекция вектора скорости на ось x, а направление бинормали к силовой линии магнитного поля в формуле (3) противоположно направлению координатной оси x. В соответствии с полученным результатом положительно заряженная частица дрейфует в положительном направлении бинормали к силовой линии магнитной индукции, а отрицательно заряженная – в отрицательном направлении.
- орт направления бинормали к силовой линии магнитной индукции. Заметим, что соотношением (2) скорость дрейфа определена как проекция вектора скорости на ось x, а направление бинормали к силовой линии магнитного поля в формуле (3) противоположно направлению координатной оси x. В соответствии с полученным результатом положительно заряженная частица дрейфует в положительном направлении бинормали к силовой линии магнитной индукции, а отрицательно заряженная – в отрицательном направлении.
Зависимости скорости дрейфа от исходной поперечной скорости частицы и параметров магнитного поля (3) можно придать следующую форму
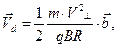 (4)
(4)
где R - радиус кривизны силовой линии векторного поля магнитной индукции. Действительно, частная производная от индукции магнитного поля по координате у в точках пространства, где нет электрического тока, может быть заменена на частную производную от величины  по продольной координате z. Если учесть, что длина элемента силовой линии ds равна произведению радиуса кривизны R на величину элементарного угла
по продольной координате z. Если учесть, что длина элемента силовой линии ds равна произведению радиуса кривизны R на величину элементарного угла 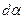 , где
, где 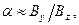 - угол наклона силовой линии к продольной координатной оси (для малых значений
- угол наклона силовой линии к продольной координатной оси (для малых значений  ), то оказывается справедливой зависимость
), то оказывается справедливой зависимость
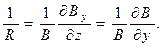 (5)
(5)
При выводе последнего соотношения учтено, что величина  (заметим, не производная!) на силовой линии равна нулю.
(заметим, не производная!) на силовой линии равна нулю.
Хотя форма записи зависимости скорости дрейфа (4) не так уж много содержит новой информации, она оказывается удобной при анализе дрейфа заряженной частицы в магнитном поле в общем случае.
Дата добавления: 2017-09-01; просмотров: 1818;











