Движение частицы в однородном магнитном поле.

В настоящем разделе ограничимся изучением движения нерелятивистских электрически заряженных частиц в однородном магнитном поле, т.е. в поле, вектор магнитной индукции 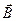которого сохраняет свою величину и направление в пространстве. Для частицы с массой 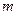и электрическим зарядом 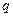уравнения движения имеют вид:

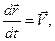
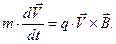(1)

Первое из этих уравнений – кинематическое определение скорости, а второе – уравнение динамики материальной точки (второй закон Ньютона) с учётом силы Лоренца. Отличительной особенностью движения заряженной частицы в магнитном поле является постоянство кинетической энергии материальной частицы, поскольку сила Лоренца не производит работы на элементарном перемещении. Действительно, умножая второе из уравнений (1) скалярно на вектор скорости, получаем:

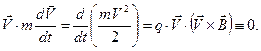(2)

Следствием полученного результата является постоянство абсолютной величины скорости частицы 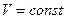в процессе движения.

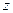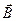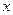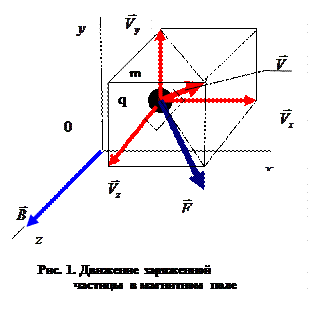
Если ось декартовой системы координат направить вдоль вектора магнитной индукции , оси и 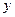направить так как показано на рис. 1, то вектор силы Лоренца будет расположен в плоскости Оху (направление силы Лоренца показано для движения положительно заряженной частицы 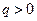),ауравнения динамики частицы примут вид:

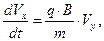
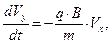
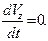(3)

Из уравнений (3) следует, что продольная скорость заряженной частицы и рассмотреть движение положительно заряженной частицы 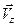, т.е. скорость вдоль направления однородного магнитного поля 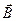, остаётся постоянной. Если в начальный момент времени эта скорость равнялась нулю 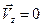, то дальнейшее движение происходит в плоскости 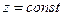, т.е. в плоскости Оxy. Исключая 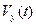из системы уравнений (3) , приходим к уравнению:

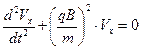. (4)

Анализируя форму записи уравнения (4), замечаем, что положительная величина

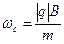(5)

является круговой частотой процесса, она имеет специальное название: «циклотронная частота». Общее решение уравнения (4) имеет вид:

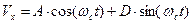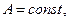
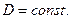, (6)

Возвращаясь к системе уравнений (3), запишем выражение для функции :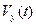

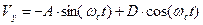, (7)

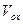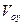Если искомые функции в начальный момент времени равнялись величинам и , постоянные интегрирования приобретают определенный физический смысл:

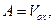
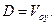(8)

Выше для общего случая было установлено, что при движении заряженной частицы в магнитном поле величина модуля скорости частицы сохраняется. Проверим это положение для рассматриваемого случая, используя зависимости (6) и (7) с учётом постоянства продольной скорости частицы:

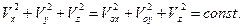(9)

Действительно, величина модуля скорости заряженной частицы в магнитном поле сохраняется.

Зависимости от времени для смещений частицы вдоль координатных осей х и у можно получить интегрированием выражений (6) и (7) соответственно с учётом начального положения частицы:

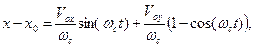
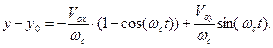(10)

Если возвести приведённые выражения в квадрат и сложить результаты, можно получить уравнение траектории заряженной частицы в однородном магнитном поле в форме смещённой окружности:

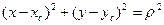, (11)

где 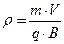- радиус круговой орбиты, 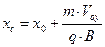и 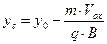- координаты центра окружности.

Интересно рассмотреть следующую форму записи выражений (6) и (7) для проекций скорости частицы на координатные направления:

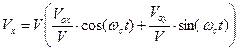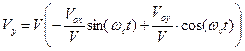, . (12)

Введём в рассмотрение вспомогательный угол 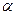соотношениями 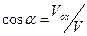, 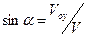и перепишем выражения (12):

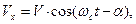
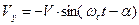. (13)

Аналогичные зависимости имеют место и для координат частицы:

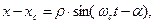
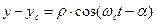. (14)

В соответствии с зависимостями (14) положительно заряженная частица вращается вокруг направления индукции магнитного поля (силовая линия поля 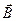проходит через точку плоскости ху с координатам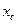и и 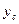) по часовой стрелке. Нетрудно убедиться, что угловая скорость вращения при этом численно совпадает с циклотронной частотой, а пространственная картина движения позволяет записать зависимость для вектора угловой скорости заряженной частицы в однородном магнитном поле :

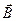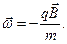(15)

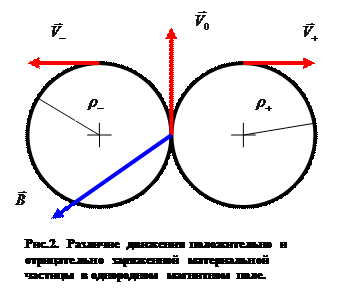Заметим, что при изменении знака электрического заряда частицы меняется на противоположное и направление вектора угловой скорости, что означает смену направления вращения частицы и, как следствие, изменение рисунка траектории частицы (рис. 2). Это явление используется в ядерной физике и физике элементарных частиц при исследовании реакций взаимодействия, рождения и распада элементарных частиц в камерах Вильсона (пузырьковые камеры с магнитным полем). По кривизне траектории частицы на фотоснимке можно определить величину и знак её удельного заряда q/m.

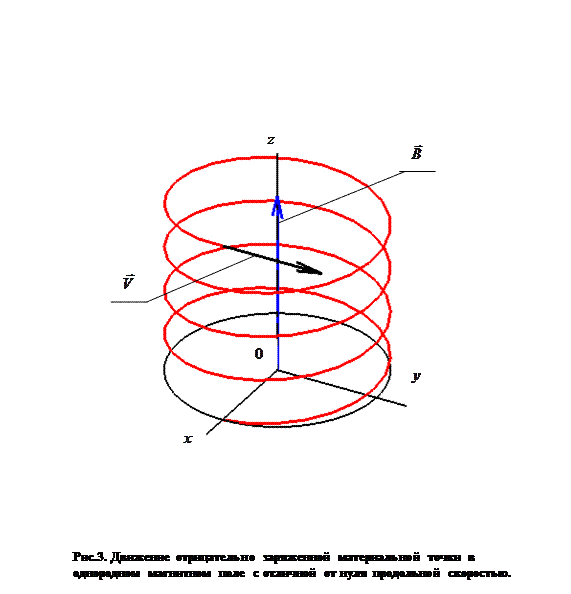
До сих пор мы рассматривали движение заряженной частицы в однородном магнитном поле без учёта её продольной скорости. В более общем случае продольное движение частицы происходит независимо от поперечного движения. Если продольная составляющая скорости постоянна по величине, траектория движения является винтовой линией с постоянным шагом, ось которой совпадает по направлению с соответствующей силовой линией. В случае переменного продольного движения частицы шаг винтовой линии становится тоже переменным. Винтовая линия оказывается «правой» или «левой» в зависимости от знака электрического заряда материальной точки. На рис. 3 приведена качественная траектория движения отрицательно заряженной частицы в однородном магнитном поле с отличной от нуля постоянной продольной скоростью. Здесь индукция магнитного поля направлена вдоль оси z, параметрические уравнения движения имеют вид

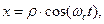
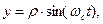
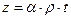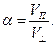, (16)

В этих соотношениях циклотронный радиус и циклотронная частота рассчитываются по модулю продольной скорости и модулю электрического заряда, величина параметра 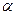, равная отношению продольной скорости к поперечной скорости частицы, может быть как положительной, так и отрицательной величиной.