Движение частицы в неоднородном магнитном поле.

В общем случае, кода магнитное поле является нестационарным и неоднородным, уравнения динамики заряженной частицы становятся либо линейными уравнениями с переменными во времени коэффициентами (случай однородного поля), либо «коэффициенты» уравнений движения оказываются функциями от искомых координат частицы и задача становится нелинейной (случай неоднородного поля). Хотя несложно получить все конкретные результаты (координаты частицы, проекции скорости на координатные направления, ориентацию элементарного отрезка траектории в окрестности рассматриваемой точки пространства) с помощью численного интегрирования системы уравнений движения с учётом силы Лоренца, выработать общее представление о движении заряженных частиц в неоднородном магнитном поле достаточно сложно. Однако, если «сильное» магнитное поле «слабо» меняется во времени и (или) в пространстве, анализ движения заряженной частицы в магнитном поле можно провести методом последовательных приближений. Суть его состоит в том, что в «нулевом» приближении считают, что частица движется в сильном однородном постоянном во времени магнитном поле. Такое движение является быстрым вращением по ларморовскому кружку, центр которого перемещается вдоль силовой линии индукции магнитного поля. В «первом приближении» учитываются

пространственные неоднородности магнитного поля как поправки к описанной картине движения. Они проявляются в том, что центр ларморовского кружка («ведущий центр» заряженной частицы) получает дополнительное, относительно медленное движение. Такое движение называют «дрейфом», его параметры суть циклотронная частота 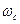, радиус ларморовского кружка 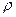, продольная 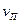и поперечная 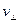скорости частицы. Приближение дрейфа удовлетворительно, если за циклотронный период 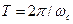изменения параметров дрейфа будут малы в сравнении с самими параметрами, а величина индукции магнитного поля мало изменяется на расстояниях, сравнимых с радиусом ларморовского кружка. В «дрейфовой» теории быстрое вращение частицы по ларморовскому кружку большого интереса не представляет, параметры его «усредняют», а во внимание принимают сглаженное движение ведущего центра.

В последние годы дрейфовая теория нашла многочисленные приложения при анализе движения космических частиц в межзвёздном пространстве, околопланетных магнитных полях, магнитных ловушках для удержания и нагрева плазмы с целью освоения управляемых термоядерных реакций.

Строгое обоснование дрейфового приближения требует применения специальных методов анализа нелинейной механики, поэтому ниже ограничимся простейшим качественным рассмотрением дрейфа заряженной частицы.