Дрейф заряженной частицы, вызванный искривлением магнитных силовых линий.

Рассмотрим дрейф условно положительно заряженной частицы в магнитном поле с искривленными силовыми линиями в предположении, что величина модуля вектора магнитной индукции меняется незначительно. Допустим, что силовая линия, проходящая через точку расположения заряженной частицы в рассматриваемый момент времени имеет вид, показанный на рис.1. В общем случае траектория частицы не обязательно совпадает 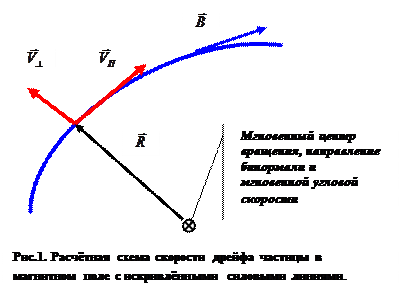с силовой линией магнитного поля, поэтому исходную скорость частицы можно разложить на продольную 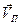и поперечную 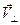составляющие относительно направления вектора индукции магнитного поля 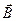. Единичные векторы главной нормали, касательного направления и бинормали к силовой линии магнитной индукции определяются выражениями:

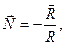
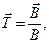
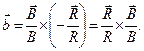(1)

Поскольку 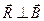по условию, вектор бинормали 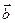является единичным.

Движение частицы вдоль силовой линии магнитного поля можно представить как вращение вокруг мгновенного центра вращения с угловой скоростью :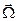

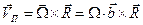. (2)

Перейдём в систему координат, которая вращается вокруг мгновенного центра вращения с угловой скоростью 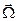(при этом, естественно, изменится и система отсчёта). В новой системе координат продольное движение частицы отсутствует, а поперечная составляющая исходной скорости частицы является относительной скоростью. Рассматриваемая система отсчёта не является инерциальной, поэтому в число сил, действующих на частицу, при описании её движения в рассматриваемой системе координат необходимо включить силу инерции и силу Кориолиса:

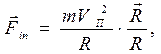
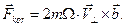(3)

Но кориолисова сила направлена параллельно вектору 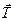, она будет изменять только продольную составляющую скорости, на параметрах дрейфа это скажется только во втором приближении. Центробежная сила инерции 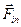обуславливает возникновение дрейфа в поперечном направлении. Скорость этого дрейфа можно рассчитать по аналогии со случаем электрического дрейфа:

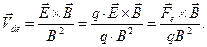(4)

Если вместо силы 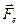, действующей на частицу со стороны электрического поля напряжённости 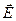, в соотношение (4) подставить выражение для центробежной силы 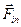в соответствии с формулой (3), получим:

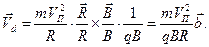(5)

В заключение анализа дрейфа заряженной частицы в электромагнитном поле запишем общую формулу для скорости ведущего центра:

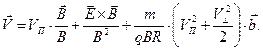(6)

Подведём итоги анализа дрейфового движения заряженной частицы в электромагнитном поле. В магнитном поле, в котором возможные пространственные и временные неоднородности выражены слабо, а электрическое поле невелико, заряженная частица относительно быстро вращается по окружности ларморовского радиуса. Ведущий центр заряженной частицы смещается вдоль силовой линии магнитного поля с продольной скоростью и в поперечном направлении со скоростью дрейфа. Этот движение определяется вторым и третьим слагаемым в правой части соотношения (6). Направление «электрического» дрейфа не зависит от знака электрического заряда, а направление «магнитного» дрейфа для положительно и отрицательно заряженных частиц происходит по направлению бинормали или против направления бинормали к силовой линии магнитного поля в зависимости от знака электрического заряда частицы.

9.3.5. Адиабатический инвариант.

Когда заряженная частица двигается в переменном и (или) неоднородном магнитном поле, параметры её движения меняются с течением времени и в зависимости от положения частицы в пространстве. Элементарный анализ этого явления можно выполнить, если считать, что величина индукции магнитного поля велика, а неоднородность магнитного поля и скорость изменения его во времени являются малыми величинами: изменение индукции магнитного поля на расстояниях, сравнимых с ларморовским радиусом, и изменение магнитного поля в течение времени, сравнимого с периодом ларморовского движения, малы по сравнению с самой величиной индукции магнитного поля.

Рассмотрим простейший случай движения заряженной частицы: магнитное поле однородно и медленно меняется с течением времени, электрическое поле отсутствует, продольной скорости частицы нет, имеется только поперечная составляющая. В постоянном магнитном поле частица двигалась бы по ларморовской окружности под действием постоянной по величине силы Лоренца. Но переменное магнитное поле порождает электрическое поле, которое изменяет траекторию и остальные параметры движения частицы. В первом приближении для выяснения характера движения частицы можно считать, что движение всё ещё происходит по ларморовской окружности. Уравнение динамики частицы в проекции на касательное направление к траектории движения имеет вид:

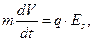(1)

где 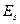- проекция напряжённости электрического поля на касательное направление к траектории. Эту величину можно определить с помощью закона электромагнитной индукции Фарадея:

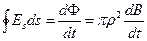. (2)

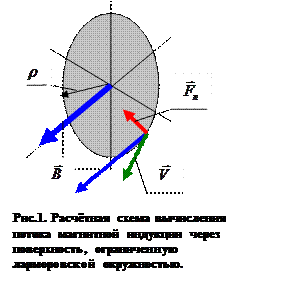
Отсутствие знака «минус» в правой части соотношения (2) легко понять из рассмотрения рис. 1. Положительное направление обхода контура при заданном направлении вектора индукции магнитного поля (и согласованного с ним направления вектора нормали к поверхности) является направлением против часовой стрелки, а положительное направление движения частицы выбрано по часовой стрелке. Поток вектора магнитной индукции через ларморовский кружок является положительной величиной, это удобно, но нужно учитывать изменение направления положительного обхода контура.

Если мы предположим, что величина 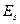мало меняется на контуре, легко получим:

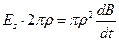
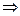
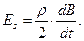(3)

Подставим полученный результат в уравнение (1) с учётом определения ларморовского радиуса:

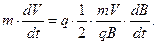(4)

Из уравнения (4) следует соотношение

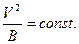(5)

По смыслу использованных при выводе соотношения (5) обозначений под величиной V следует понимать величину 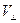- величину поперечной скорости частицы. В приближении теории дрейфа величина 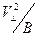является постоянной величиной, она сохраняется в процессе движения. Её называют адиабатическим инвариантом движения. Соотношение (5) справедливо только при медленных изменениях магнитного поля с течением времени, точным интегралом движения оно не является. Можно показать, что оно остаётся справедливым и при малой величине пространственной неоднородности магнитного поля.

Следствием соотношения (5) является явление отражения заряженной частицы от области с большой величиной магнитной индукции. Объяснение этого явления заключается в том, что в дрейфовом приближении в отсутствие внешнего электрического поля кинетическая энергия заряженной частицы сохраняется, значит, сохраняется и величина квадрата модуля скорости частицы:

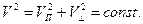(6)

В сочетании с зависимостью (5) получаем

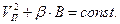(7)

Здесь 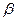- некоторая постоянная величина. При увеличении магнитной индукции В значение продольной скорости 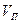уменьшается и в предельном случае может достичь нуля, частица останавливается в продольном движении и в результате флуктуации состояния начинает движение в обратном направлении. Описанное явление используется при создании магнитных ловушек для удержания плазмы в экспериментальных установках для исследования термоядерных реакций.