Графическая иллюстрация безразмерных (относительных) зависимостей

На рисунке 3 приведены графики изменения во времени касательных компонент векторов напряжённости электрического поля падающей, отражённой и преломлённой волн для s-поляризации падающей электромагнитной волны. Величины напряжённости электрического поля отнесены к величине амплитуды напряжённости электрического поля падающей волны, по оси абсцисс отложена величина 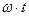, процесс колебаний в начале координат показан в течение двух периодов электромагнитной волны. Угол падения электромагнитной волны равен 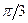, относительный показатель преломления n=0,5. Приведённые графики описывают изменение во времени напряжённостей магнитного поля для 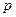- поляризации падающей электромагнитной волны

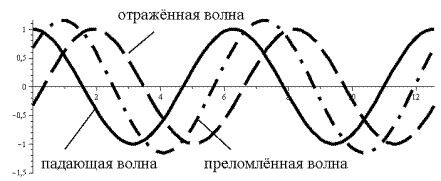
Рис. 3. Силовые факторы электромагнитной волны.

На рис. 3 прослеживается факт выполнения условий сопряжения электромагнитных полей на поверхности раздела сред.

На рис4. приведены графические зависимости изменения во времени мгновенных значений нормальных составляющих векторов Умова-Пойнтинга падающей, отражённой и преломлённой волн для s-поляризации падающей электромагнитной волны. Угол падения равен величине 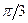, относительный показатель преломления n=0.5. По оси абсцисс отложена величина 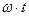, нормальная составляющая вектора Умова-Пойнтинга падающей волны нормирована на единицу.

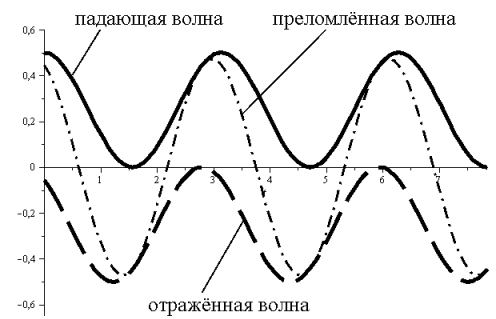
Рис. 4. Нормальные к поверхности раздела сред мгновенные

составляющие векторов Умова-Пойнтига.

На рис. 4 следует обратить внимание на выполнение баланса плотности потоков электромагнитной энергии в каждый момент времени.

На рис. 5 показано влияние угла падения а на нормальные составляющие векторов Умова-Пойнтинга падающей, отражённой и преломлённой волн для точки наблюдения в начале координат в начальный момент времени для случая n=0,5 и s-поляризации падающей волны.

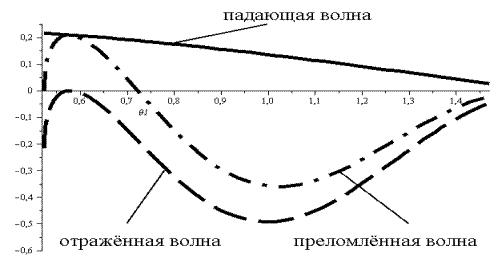
Рис. 5. Влияние угла падения на величины нормальных составляющих плотности потока энергии в точке наблюдения начало координат в начальный момент времени.

Вывод:

Основные результаты теории полного внутреннего отражения плоской гармонической электромагнитной волны на границе раздела двух диэлектриков получены без дополнительной гипотезы о том, что в классических формулах Френеля можно использовать комплексные тригонометрические функции. Показано, что в течение периода электромагнитной волны на поверхности раздела двух диэлектриков баланс плотностей потоков электромагнитной энергии, перпендикулярных поверхности раздела, выполняется для каждого момента времени.

Литература.

1. Стрэттон Дж. А. Теория электромагнетизма. –М.: ГТТИ, 1948. (Stratton J.A. Electromagnetic Theory,ch IX – N.-Y.: McGraw-Hill. 1941).
2. Борн М., Вольф Э. Основы оптики. – М.: НАУКА, ГРФМЛ, -1970. 856 с.
3. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Электродинамика сплошных сред. – М.: ГИФМЛ. – 1959. – 532с.
4. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика в 10 т. Том VIII. Электродинамика сплошных сред. - Изд третье, исправл. – М.: НАУКА. ГРФМЛ. – 1992. – 662с.
5. Сивухин Д.В. Оптика: Учебн. пособие. – 2-е изд. испр. – М.: НАУКА, ГРФМЛ. -1985 -752 с., ил. (Общ. курс физики).
6. Эйхенвальд А. О движении энергии при полном внутреннем отражении. – М.: Известия императорского московского инженерного училища, часть 2, выпуск 2. – 1908.
7. Мандельштам Л.И. //Phys. Z. - 15. – 220. -1914. (Полное собрание трудов, изд-во АН СССР, -1948. –т.1. –стр. 261).
8. Макаров А.М., Лунёва Л.А., Макаров К.А. О сопряжении плоских гармонических волн на поверхности раздела в классической электродинамике. //Вестник МГТУ им. Н.Э.Баумана.Сер. Естественные науки. -2008. - №3. –С.29-36.
9. Макаров А.М., Лунёва Л.А., Макаров К.А. О некоторых эффектах при падении плоской гармонической волны на границу раздела диэлектрик-проводник. //Вестник МГТУ им. Н.Э.Баумана.Сер. Естественные науки. -2009. - №2(33). –С.57-71.