Цилиндрический конденсатор.

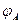
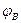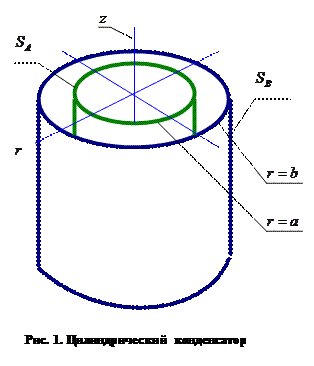
Допустим, что область D представляет собой пространство между двумя коаксиальными цилиндрическими проводящими поверхностями, размеры которых в осевом направлении велики по сравнению с величинами радиусов описываемых поверхностей и величиной зазора между ними (b-a). Потенциалы обкладок конденсатора являются постоянными заданными величинами и . В настоящем случае удобно использовать цилиндрическую систему координат ( 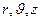), ось z при этом направить вдоль оси цилиндрических поверхностей (рис. 1).

Уравнение Лапласа для потенциала электростатического поля в области D имеет вид:

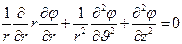в D . (1)

Уравнение (1) можно существенно упростить, если учесть условие осевой симметрии задачи ( 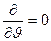) и «бесконечную протяженность» конструкции вдоль оси z. В последнем случае две точки области D, отличающиеся значениями координаты z, одинаково удалены от краев цилиндрических поверхностей, поэтому можно считать, что выполняется условие 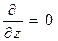. В итоге уравнение (1) принимает вид:

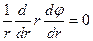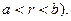, ( (2)

С учетом граничных условий

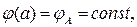
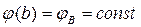(3)

решение уравнения (2) можно записать в форме:

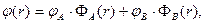(4)

где

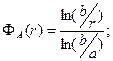
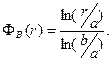(5)

Вычислим производную от 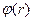- соотношения (4)-(5) – по радиальной координате:

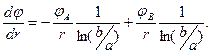(6)

Рассмотрим внешнюю обкладку конденсатора 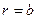. Направление нормали к поверхности раздела с плотностью заряда 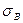выберем вдоль поперечной координаты. Учтём, что в пространстве вне конденсатора напряжённость электростатического поля равна нулю. При этом 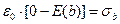, 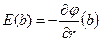и соотношение (6) позволяет рассчитать величину поверхностной плотности электрического заряда на соответствующей обкладке цилиндрического конденсатора:

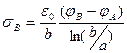(7)

и погонную плотность электрического заряда (т.е. величину электрического заряда в пересчёте на единицу длины конденсатора вдоль оси z)

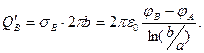(8)

Поскольку было принято, что 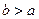, то знак величины 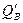определен знаком разности потенциалов 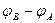. В этом случае величина ёмкости цилиндрического конденсатора в пересчете на единицу длины вдоль продольной оси имеет вид:

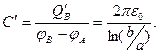(9)

Следует обратить внимание на принципиальную разницу между зависимостями (9) и (20) раздела 3.4.1: при изучении электростатического поля цилиндрического конденсатора нет необходимости выбирать в качестве опорного значения потенциал бесконечно удалённой точки.

Проанализируем физические размерности величин, входящих в выражение (9). Размерность величины погонной плотности электрического заряда 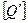равна 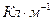, поэтому размерность погонной ёмкости цилиндрического конденсатора 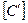равна 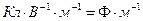. Поскольку под знаком логарифма в выражении (9) стоит безразмерная величина, то размерность электрической постоянной 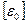должна быть равна .

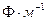В рассматриваемом случае, так же как и в случае плоского конденсатора, уменьшение зазора между обкладками конденсатора ( 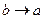) приводит к увеличению ёмкости конденсатора. Если заметить, что формально 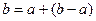, и в условиях малого зазора между обкладками конденсатора имеет место соотношение 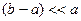, можно воспользоваться первыми членами разложения в ряд Тэйлора для зависимости 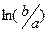в окрестности :

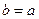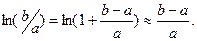(10)

С учетом последнего приближенного результата получаем, что при очень малом зазоре между обкладками цилиндрического конденсатора из соотношения (9) следует зависимость:

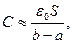(11)

где 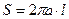- площадь обкладки, 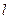- продольный размер конденсатора. По форме записи выражение (11) идентично формуле (9) предыдущего раздела для ёмкости плоского конденсатора. Исходя из этого результата, можно полагать, что это соотношение будет справедливо для произвольного конденсатора с постоянным малым зазором между обкладками.