Мкость уединённого проводника.
Уединённыйпроводник ограниченных размеров и произвольной формы в безграничном однородном пространстве обладает «электрической ёмкостью». Это понятие является следствием возможности накапливать электрический заряд на наружной поверхности проводника. Величина электрического заряда проводника и потенциал его поверхности связаны между собой линейной зависимостью. Допустим, что проводник находится в вакууме, а бесконечно удалённая от его поверхности точка пространства обладает нулевым потенциалом. Электрической ёмкостью или просто ёмкостью проводника принято считать отношение заряда проводника к потенциалу его поверхности:
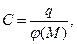
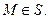 (1)
(1)
Здесь 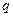 - электрический заряд проводника,
- электрический заряд проводника, 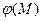 - потенциал электростатического поля в произвольной точке
- потенциал электростатического поля в произвольной точке 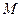 поверхности
поверхности 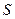 проводника.
проводника.
Поскольку значение потенциала поверхности проводника определено выбором значения потенциала бесконечно удалённой точки, можно подумать, что значение электрической ёмкости зависит от этого выбора. Правильное представление о физической сути введённого понятия заключается в том, что 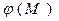 представляет собой разность потенциала поверхности проводника и потенциала бесконечно удалённой точки пространства. Приписать потенциалу бесконечно удаленной точки определенное значение не всегда удаётся. Определение электрической ёмкости (ГОСТ 19880-74. Электротехника. Основные понятия. Термины и определения. –М.-1976) звучит так:
представляет собой разность потенциала поверхности проводника и потенциала бесконечно удалённой точки пространства. Приписать потенциалу бесконечно удаленной точки определенное значение не всегда удаётся. Определение электрической ёмкости (ГОСТ 19880-74. Электротехника. Основные понятия. Термины и определения. –М.-1976) звучит так:
Электрическая ёмкость уединённого проводника равна отношению заряда 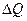 , внесённого на проводник, к приращению потенциала
, внесённого на проводник, к приращению потенциала 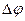 этого проводника.
этого проводника.
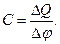 (2)
(2)
В этом определении величина потенциала бесконечно удалённой точки не имеет принципиального значения (при этом молчаливо подразумевается, что изменение заряда проводника на малую величину 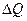 не сказывается на величине потенциала бесконечно удалённой точки).
не сказывается на величине потенциала бесконечно удалённой точки).
Электрическая ёмкость является размерной величиной [C]=[q]/[ 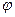 ], в системе СИ это отношение равно Кл/В и ему присвоено специальное название - «фарад»: 1 Ф – это ёмкость конденсатора, разность потенциалов обкладок которого составляет величину 1 В при заряде конденсатора 1 Кл. Фарад – очень большая величина ёмкости, на практике используются дольные величины ёмкости: мФ, мкФ, нФ и пФ.
], в системе СИ это отношение равно Кл/В и ему присвоено специальное название - «фарад»: 1 Ф – это ёмкость конденсатора, разность потенциалов обкладок которого составляет величину 1 В при заряде конденсатора 1 Кл. Фарад – очень большая величина ёмкости, на практике используются дольные величины ёмкости: мФ, мкФ, нФ и пФ.
Ёмкость уединённого проводника является положительной величиной и полностью определяется геометрией поверхности проводника и электрическими свойствами окружающего пространства. Действительно, на поверхности заряженного проводника находится поверхностная плотность электрического заряда 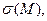
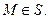 Величина электрического заряда проводника определена соотношением
Величина электрического заряда проводника определена соотношением
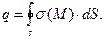 (3)
(3)
В силу принципа суперпозиции для потенциала произвольной точки пространства 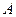 можно записать выражение:
можно записать выражение:
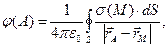 (4)
(4)
где 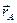 и
и 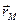 - радиус-векторы соответствующих точек пространства. Но это выражение должно быть справедливо и для произвольной точки поверхности проводника, только в этом случае должно выполняться условие
- радиус-векторы соответствующих точек пространства. Но это выражение должно быть справедливо и для произвольной точки поверхности проводника, только в этом случае должно выполняться условие 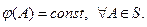 Если справедлива зависимость
Если справедлива зависимость
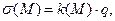 (5)
(5)
то функция формы проводника 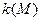 удовлетворяет условию
удовлетворяет условию
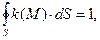 (6)
(6)
а потенциал поверхности проводника приобретает вид:
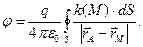 (7)
(7)
В соответствии с определением понятия ёмкости проводника получаем:
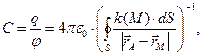

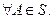 (8)
(8)
Таким образом, электрическая ёмкость уединённого проводника произвольной формы в вакууме зависит только от геометрии проводника.
Вычислим электрическую ёмкость уединённого проводящего шара радиуса а в соответствие с зависимостью (8). С учетом симметрии поверхности проводника для функции формы имеет место соотношение:
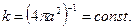 (9)
(9)
Положение точки А на сфере может быть произвольным, поэтому выберем его так, что составляющие радиус-вектора этой точки в декартовой системе координат приобретают вид:
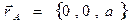 . (10)
. (10)
Проекции радиус-вектора произвольной точки М на сфере имеют вид:
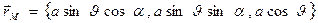 . (11)
. (11)
Знаменатель подынтегральной функции в формуле (8) в этом случае равен
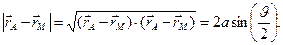 (12)
(12)
Вычислим интеграл:
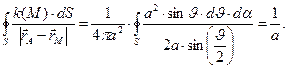 (13)
(13)
В итоге получаем известную формулу для ёмкости шара
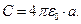 (14)
(14)
Конечно, этот результат можно получить значительно более просто: по теореме Гаусса определить зависимость напряжённости поля 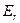 от расстояния, интегрированием получить зависимость потенциала для произвольной точки пространства и точки поверхности шара и рассчитать величину электрической ёмкости шара в соответствии с определением. К сожалению, этот путь приемлем только для проводников с высокой степенью симметрии формы.
от расстояния, интегрированием получить зависимость потенциала для произвольной точки пространства и точки поверхности шара и рассчитать величину электрической ёмкости шара в соответствии с определением. К сожалению, этот путь приемлем только для проводников с высокой степенью симметрии формы.
Для проводящего эллипсоида, поверхность которого описывается уравнением
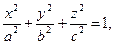 (15)
(15)
где для определённости 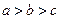 , величина электрической ёмкости равна
, величина электрической ёмкости равна
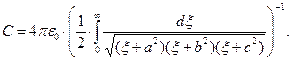 (16)
(16)
Интеграл в этом соотношении не выражается через элементарные функции, его можно выразить через табулированные эллиптические интегралы достаточно сложных аргументов, а можно воспользоваться системой символьных вычислений Maple или Mathematica современного специального математического обеспечения персональных компьютеров и получить значение ёмкости С проводящего эллипсоида для произвольного сочетания значений a, b и c.
Для случая 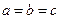 эллипсоид превращается в шар, при этом из зависимости (16) следует результат (14). Для двухосного эллипсоида (эллипсоид вращения) зависимость ёмкости от геометрических параметров проводника выражается через элементарные функции. Так для вытянутого эллипсоида вращения
эллипсоид превращается в шар, при этом из зависимости (16) следует результат (14). Для двухосного эллипсоида (эллипсоид вращения) зависимость ёмкости от геометрических параметров проводника выражается через элементарные функции. Так для вытянутого эллипсоида вращения 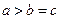 имеет место зависимость:
имеет место зависимость:
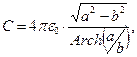 (17)
(17)
а для сплюснутого эллипсоида вращения 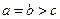 ёмкость может быть рассчитана по формуле
ёмкость может быть рассчитана по формуле
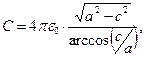 (18)
(18)
в частности, для диска 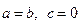 имеет место зависимость
имеет место зависимость
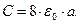 (19)
(19)
Для практического определения величины электрической ёмкости проводника заданной формы придётся предварительно решить уравнение Лапласа для внешнего по отношению к проводнику пространства с условием, что потенциал принимает на поверхности проводника постоянное значение, затем вычислить суммарный заряд проводника и воспользоваться определением (2). Для проводников канонических форм (шар, например) описанная процедура не представляет особой сложности. Для «точечного» проводника потенциал его поверхности обращается в бесконечность при конечной величине сосредоточенного заряда, поэтому ёмкость такого объекта равна нулю.
Попытка определить ёмкость уединённого бесконечного проводящего цилиндра (хотя бы и в расчёте на единицу длины) соотношением
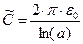 , (20)
, (20)
где а – радиус поперечного сечения цилиндра, физически несостоятельна. Действительно, размерность погонной ёмкости такого проводника «фарад на метр» обеспечивается размерностью электрической постоянной 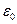 , под знаком логарифма должна находиться безразмерная величина, а второго характерного линейного размера в рассматриваемой расчётной схеме нет. Зависимость (20) и при малых и при больших значениях радиуса цилиндра приводит к результатам, не обладающим физическим содержанием. Попытка заменить логарифм радиуса цилиндра модулем логарифма к успеху не приводит. Заметим, что для конденсатора из двух бесконечных проводящих поверхностей с достаточно произвольной формой поперечного сечения существует возможность расчёта погонной ёмкости.
, под знаком логарифма должна находиться безразмерная величина, а второго характерного линейного размера в рассматриваемой расчётной схеме нет. Зависимость (20) и при малых и при больших значениях радиуса цилиндра приводит к результатам, не обладающим физическим содержанием. Попытка заменить логарифм радиуса цилиндра модулем логарифма к успеху не приводит. Заметим, что для конденсатора из двух бесконечных проводящих поверхностей с достаточно произвольной формой поперечного сечения существует возможность расчёта погонной ёмкости.
3.4.2. Ёмкость конденсатора.
3.4.2.1. Ёмкость конденсатора произвольной формы.
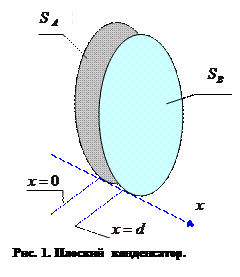
Пусть замкнутая простая достаточно гладкая, в остальном, произвольная, проводящая поверхность SB охватывает без точек соприкосновения замкнутую простую достаточно гладкую, в остальном произвольную, проводящую поверхность SA как показано на рис.1 . Пусть область изменения независимых переменных D – множество внутренних точек M области D – представляет собой пространство, заключенное между поверхностями SA и SB. Очевидно, что границей области D служит объединение поверхностей SA и SB:
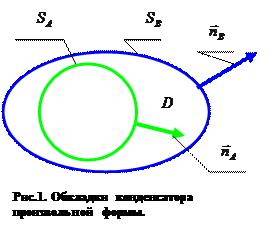
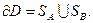 (1)
(1)
 Пусть в области D относительная диэлектрическая проницаемость равна единице, на поверхности SA поддерживается заданное значение электрического потенциала
Пусть в области D относительная диэлектрическая проницаемость равна единице, на поверхности SA поддерживается заданное значение электрического потенциала 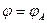 , на поверхности SB – значение
, на поверхности SB – значение 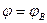 . Если в области D отсутствует объёмная плотность свободного электрического заряда, распределение электрического потенциала в области D, как известно, является решением следующей математической задачи:
. Если в области D отсутствует объёмная плотность свободного электрического заряда, распределение электрического потенциала в области D, как известно, является решением следующей математической задачи:
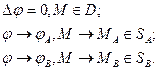 (2)
(2)
Оператор 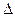 в формулировке задачи (2) является оператором Лапласа, граничные условия понимаются как «предельные», точка М приближается к граничным поверхностям из области D. Поскольку на границе области D заданы значения искомой функции, задача (2) получила название «краевая задача первого рода (или задача Дирихле) для уравнения Лапласа в области D.
в формулировке задачи (2) является оператором Лапласа, граничные условия понимаются как «предельные», точка М приближается к граничным поверхностям из области D. Поскольку на границе области D заданы значения искомой функции, задача (2) получила название «краевая задача первого рода (или задача Дирихле) для уравнения Лапласа в области D.
Решение задачи (2) можно записать с помощью функции Грина:
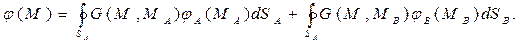 (3)
(3)
С методами построения функции Грина можно познакомиться по учебникам математической физики. Для дальнейшего изложения важно обратить внимание на то, что функция Грина зависит только от положения точки наблюдения М и положения источника поля – точки МА или точки МВ. Поскольку в настоящем разделе поверхности SA и SB являются проводящими, электрическое поле является статическим, то имеют место соотношения:
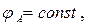

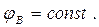 (4)
(4)
С учетом соотношений (3.87) распределение электрического потенциала в области D можно переписать в форме:
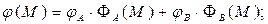 (5)
(5)
где
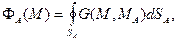
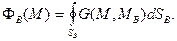 (6)
(6)
Заметим, что соотношения (6) в простейших случаях можно получить, не прибегая к построению функции Грина. Ниже это будет показано для плоского, цилиндрического и сферического конденсаторов.
Если 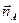 и
и 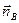 - орты внешних нормалей к элементам поверхностей SA и SB соответственно, то решение рассматриваемой задачи обладает свойством:
- орты внешних нормалей к элементам поверхностей SA и SB соответственно, то решение рассматриваемой задачи обладает свойством:
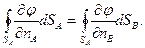 (7)
(7)
Доказать свойство (7) несложно. Первый способ доказательства состоит из следующих шагов. Запишем уравнение Лапласа в дивергентной форме:
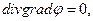 (8)
(8)
проинтегрируем его по объёму (область D):
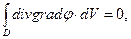 (9)
(9)
воспользуемся теоремой Остроградского-Гаусса и перейдем от интеграла по объёму к интегралу по замкнутой поверхности, ограничивающей этот объём:
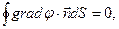 (10)
(10)
используем обозначение
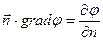 (11)
(11)
и получим
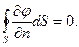 (12)
(12)
Осталось только вспомнить, что здесь замкнутая поверхность S состоит из двух частей, SA и SB, причем внешняя по отношению к замкнутой поверхности SB нормаль к элементу dSB совпадает с нормалью 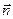 , а внешняя по отношению к замкнутой поверхности SA нормаль к элементу dSA – противоположна вектору
, а внешняя по отношению к замкнутой поверхности SA нормаль к элементу dSA – противоположна вектору 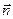 . Свойство (7) доказано.
. Свойство (7) доказано.
Второй способ физически более нагляден. Если догадаться, что
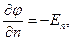 (13)
(13)
где 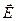 - вектор напряженности электростатического поля, то правая и левая части свойства (7) – это потоки вектора
- вектор напряженности электростатического поля, то правая и левая части свойства (7) – это потоки вектора 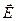 через соответствующие замкнутые поверхности, взятые с обратным знаком. Поскольку в области D, ограниченной поверхностями SA и SB нет электрических зарядов, в соответствии с теоремой Гаусса для вектора напряженности электростатического поля должно иметь место соотношение (7).
через соответствующие замкнутые поверхности, взятые с обратным знаком. Поскольку в области D, ограниченной поверхностями SA и SB нет электрических зарядов, в соответствии с теоремой Гаусса для вектора напряженности электростатического поля должно иметь место соотношение (7).
Для конденсатора характерно то, что электрические заряды обкладок конденсатора (поверхности SA и SB) равны по величине и противоположны по знаку, при этом напряженность электрического поля обращается в нуль вне области D. С учетом этого обстоятельства из соотношений для нормальных составляющих вектора напряженности на границе раздела сред получаем выражения для поверхностных плотностей электрического заряда на поверхностях SA и SB:
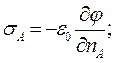
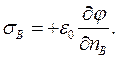 (14)
(14)
Соотношения (14) позволяют вычислить суммарные величины электрических зарядов на поверхностях SA и SB:
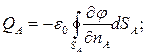
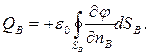 (15)
(15)
Свойство (7) позволяет убедиться, что вычисленные значения электрических зарядов действительно равны по величине и противоположны по знаку.
Ёмкость конденсатора определяют как положительный коэффициент пропорциональности между абсолютной величиной электрического заряда на одной из обкладок конденсатора и модулем разности электрических потенциалов на обкладках конденсатора (эту величину называют «напряжением»):
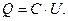 (16)
(16)
Ёмкость конденсатора определяется только геометрией (как в рассматриваемом случае) и диэлектрическими свойствами среды в пространстве между обкладками конденсатора.
Поскольку потенциал электростатического поля определён с точностью до произвольной постоянной, значение потенциала на внешней обкладке конденсатора можно положить равным нулю. Значение потенциала на внутренней обкладке конденсатора удобно считать положительной величиной. При этих условиях выражение для ёмкости конденсатора принимает вид:
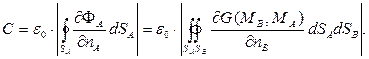 (17)
(17)
Последнее выражение доказывает независимость ёмкости конденсатора от зарядов обкладок и значений потенциалов на обкладках конденсатора.
Значение выражения (17) состоит в том, что показана теоретическая возможность (не совсем удобная в практическом отношении) рассчитать непосредственно ёмкость произвольного конденсатора. Заметим, что с появлением персональных компьютеров и специализированных пакетов математического моделирования типа Matlab, SolidWorks, ANSYS и им подобных численное решение задачи Дирихле применительно к проблемам электростатики перестало быть слишком обременительным делом.
Рассмотрим простейшие частные случаи.
 3.4.2.2.Плоский конденсатор.
3.4.2.2.Плоский конденсатор.
Допустим, что область D представляет собой пространство между двумя проводящими параллельными друг другу плоскостями, продольные размеры которых велики по сравнению с расстоянием между пластинами d. Потенциалы пластин являются постоянными заданными величинами. Система координат и расположение обкладок конденсатора показаны на рис.1. В рассматриваемом случае уравнение Лапласа для потенциала электростатического поля имеет вид (декартова система координат!):
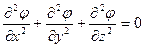 , в D. (1)
, в D. (1)
Уместно предположить, что распределение потенциала зависит только от поперечной координаты 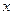 . В основе такого предположения лежит то обстоятельство, что произвольные точки пространства с различными значениями координат
. В основе такого предположения лежит то обстоятельство, что произвольные точки пространства с различными значениями координат 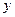 и
и 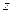 ничем не отличаются друг от друга по положению относительно «бесконечно удаленных» краёв пластин. Уравнение (1) с учетом сказанного можно записать в виде:
ничем не отличаются друг от друга по положению относительно «бесконечно удаленных» краёв пластин. Уравнение (1) с учетом сказанного можно записать в виде:
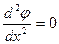 , (0<x<d), (2)
, (0<x<d), (2)
а его решение – в окончательной форме:
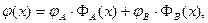 (3)
(3)
где
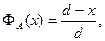
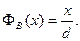 (4)
(4)
Легко видеть, что выполнены следующие соотношения:
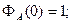
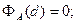
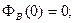
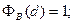 (5)
(5)
что обеспечивает выполнение условий
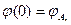
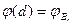 . (6)
. (6)
Заметим, что явные выражения для функций 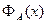 и
и 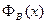 получены без построения функции Грина.
получены без построения функции Грина.
Проведённые выкладки имеет смысл сопоставить с расчётной схемой конденсатора (рис.2). Эта схема ниже будет использована при анализе конденсатора цилиндрической формы и сферического конденсатора. В настоящем разделе приняты обозначения 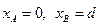 ,
, 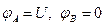 . В соответствии с соотношениями (6) имеет место
. В соответствии с соотношениями (6) имеет место
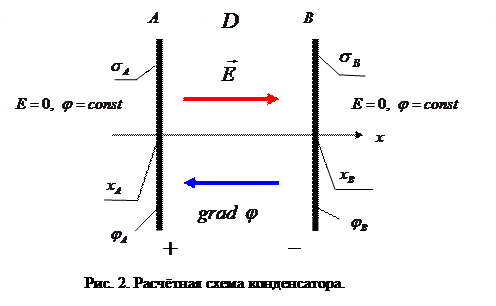
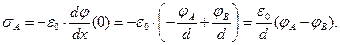 (7)
(7)
Соотношение (7) требует пояснения. Левая обкладка конденсатора представляет собой поверхность раздела сред. На этой поверхности по предположению распределён электрический заряд с плотностью 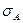 . Направление нормали к поверхности раздела можно выбрать произвольно, выберем это направление вдоль координаты х. В этом случае известное соотношение для нормальных компонент вектора напряжённости электростатического поля надо записать с учётом того, что
. Направление нормали к поверхности раздела можно выбрать произвольно, выберем это направление вдоль координаты х. В этом случае известное соотношение для нормальных компонент вектора напряжённости электростатического поля надо записать с учётом того, что 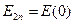 ,
, 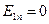 , и учесть определение вектора напряжённости электростатического поля через распределение потенциала.
, и учесть определение вектора напряжённости электростатического поля через распределение потенциала.
Если пластины конденсатора имеют площадь поверхности S (каждая пластина!), то, не учитывая концевые эффекты, получим:
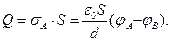 (8)
(8)
Выражение для ёмкости плоского конденсатора с площадью пластины S и расстоянием между пластинами 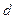 имеет вид:
имеет вид:
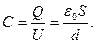 (9)
(9)
Пример учета концевых эффектов для плоского конденсатора можно найти в учебниках по уравнениям математической физики.
Из соотношения (9) следует, что с увеличением расстояния между пластинами плоского идеального конденсатора его ёмкость уменьшается пропорционально обратной величине указанного расстояния. Практически выгодно уменьшать расстояние между пластинами конденсатора, величина ёмкости конденсатора при этом заметно растёт. Минимальное расстояние d ограничено возможным электрическим пробоем пространства между обкладками конденсатора.
Дата добавления: 2017-09-01; просмотров: 2348;











