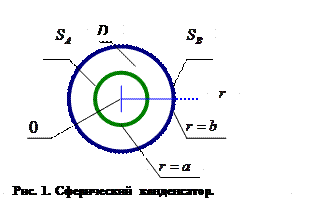
Сферический конденсатор.

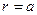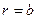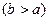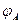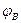Допустим, что область D представляет собой пространство между двумя концентрическими проводящими сферами радиусов и соответственно . Потенциалы обкладок сферического конденсатора являются постоянными заданными величинами - и .Уравнение Лапласа для потенциала 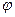электростатического поля в области D (рис. 1) в сферической системе координат имеет вид:

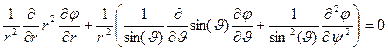в D. (1)

При записи уравнения (1) независимая переменная 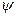играет роль азимутальной координаты.

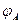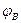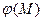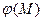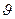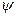Поскольку величины и не изменяются от точки к точке на соответствующих поверхностях, распределение потенциала в области D является «сферически симметричным», т.е. значение потенциала не зависит от угловых переменных и . Уравнение (1) при этом принимает вид:

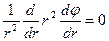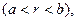, (2)

а граничные условия записываются в форме:

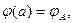
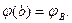(3)

Решение задачи (2)-(3) имеет вид:

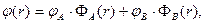(4)

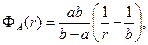
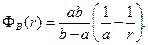(5)

Выражения (4)-(5) позволяют рассчитать значения поверхностной плотности электрического заряда на обкладках конденсатора:

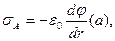
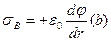(6)

и величины соответствующих электрических зарядов:

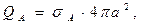
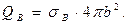(7)

В частности, для величины электрического заряда на внутренней обкладке конденсатора получаем:

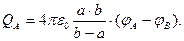(8)

Поскольку знак величины электрического заряда 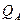определяется знаком разности потенциалов 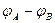, выражение для ёмкости сферического конденсатора имеет вид:

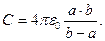(9)

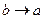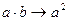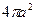
При получаем: , - это площадь поверхности внутренней обкладки конденсатора, величина 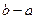является аналогом величины 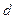в плоском конденсаторе… Итогом этого рассуждения является соотношение

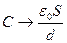при 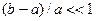. (10)

Ещё раз можно убедиться в том, что конденсатор с малым постоянным зазором подобен идеальному плоскому конденсатору.

В заключение отметим, что успех при решении рассмотренных задач обусловлен высокой степенью симметрии постановки задач, только в этом случае удается избежать построения функции Грина для заданной области изменения независимых переменных. В случае отсутствия симметрии приходится рассчитывать величину ёмкости конденсатора, следуя общему методу. Добавим к сказанному, что заменой величины 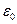на величину 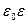, где 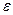- относительная диэлектрическая проницаемость однородной среды, из выражений для ёмкости «пустого» конденсатора можно получить ёмкость конденсатора, заполненного однородным диэлектриком. Расчет конденсатора с неоднородным диэлектриком основан на решении уравнения, более сложного, чем уравнение Лапласа, основы метода при этом сохраняются. Практические результаты часто проще получить применением численных методов решения соответствующей краевой задачи.

Расчёт ёмкости плоского, цилиндрического и сферического конденсаторов, заполненных неоднородным диэлектриком, свойства которого зависят только от поперечной координаты, можно выполнить с использованием теоремы Остроградского-Гаусса в интегральной форме. Применение указанного метода описано в разделе 4.7.

3.4.3. Система заряженных проводящих тел в безграничном пространстве.Пусть в конечной области безграничного пространства с относительной диэлектрической проницаемостью 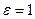расположено конечное число 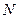заряженных проводящих тел конечного объёма, ограниченных замкнутыми достаточно гладкими поверхностями (рис. 1). Допустим, что описанные тела не касаются друг друга. Величины электрических зарядов 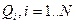на этих телах, естественно, как-то связаны с величинами электростатических потенциалов этих тел 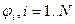. Ниже попытаемся установить эту связь.

Если 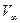- неограниченная область изменения независимых переменных, 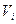- область изменения независимых переменных, описывающих заряженное проводящее тело с индексом 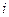, 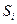- граничная поверхность описываемого тела, то область 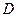можно определить соотношением:

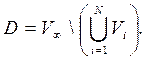(1)

В соответствии с выражением (1) область 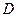изменения независимых переменных определена как дополнение к объединению объёмов заряженных тел до безграничного пространства. Задача о распределении потенциала электростатического поля в области 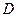включает в себя уравнение Лапласа

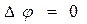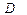в (2)

и систему граничных условий

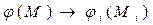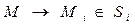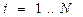, , (3)

с дополнительным условием

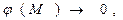
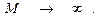(4)

Описанная задача также как и в предыдущих случаях настоящего раздела является краевой задачей первого рода или задачей Дирихле для уравнения Лапласа в области 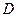. Решение рассматриваемой задачи представляет определенные трудности, но они не являются непреодолимыми. Ниже нам будет достаточно знать, что искомое решение можно записать в конечной форме с помощью функции Грина:

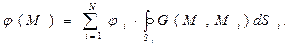(5)

Если формально вычислить производную от функции 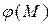по внешней нормали к элементу граничной поверхности проводящего тела с индексом 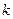(понимаемую как предел соответствующего выражения при стремлении точки наблюдения к граничной точке из области )

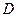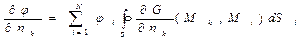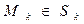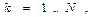, , (6)

то можно рассчитать величину электрического заряда на каждом проводящем теле:

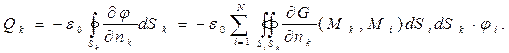(7)

Соотношением (7) определены так называемые «ёмкостные» коэффициенты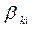

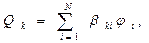
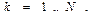(8)

а система соотношений (8) является «второй группой формул Максвелла».

Конечную систему линейных алгебраических уравнений (8) можно разрешить относительно потенциалов заряженных тел:

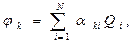
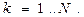(9)

Легко видеть, что матрица 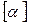с компонентами 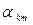является обратной для матрицы 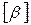с компонентами 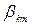. Соотношения (9) называют «первой группой формул Максвелла», а компоненты матрицы 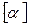- потенциальными коэффициентами.

Физический смысл ёмкостных коэффициентов состоит в следующем. Пусть для всех заряженных тел системы электрические потенциалы равны нулю за исключением одного фиксированного тела:

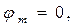
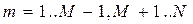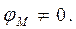, (10)