Соотношение (8) при этом приобретает вид

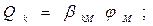(11)

что позволяет сказать, что ёмкостный коэффициент 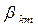численно равен электрическому заряду на проводящем теле с порядковым номером 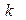при условии, что электрические потенциалы всех остальных заряженных тел системы равны нулю кроме электрического потенциала, равного единице, на проводящем теле с порядковым номером .

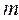Подобным образом устанавливается физический смысл и потенциальных коэффициентов. Более того, приведенные рассуждения являются основой как экспериментального, так и теоретического определения указанных коэффициентов. Последнее часто предполагает использование численных методов моделирования электростатических полей.

В качестве примера использования понятия «ёмкостные коэффициенты» рассмотрим задачу по определению ёмкости системы двух проводящих тел при условии, что электрический заряд первого тела равен по величине электрическому заряду второго тела и отличается от последнего знаком заряда. Рассматриваемая система проводящих тел отличается от классической схемы «конденсатора» тем, что поверхность одного из тел не охватывает поверхность второго тела. Допустим, что из предварительного анализа нам известна матрица ёмкостных коэффициентов 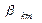. В силу общей теории справедливы соотношения:

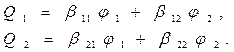(12)

Воспользуемся условием равенства нулю общего электрического заряда системы

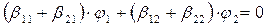, (13)

откуда следует:

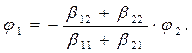(14)

Зависимость (14) позволяет вычислить разность потенциалов второго и первого тела:

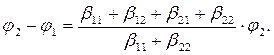(15)

Полученные зависимости позволяют рассчитать ёмкость рассматриваемой системы:

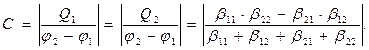(16)

Легко видеть, что соотношение (16) инвариантно относительно смены индексов тел системы.

В заключение раздела заметим, что сложность практического использования изложенной теории обусловлена в немалой степени тем, что электрические заряды (в отличие от массы твердого тела в теории тяготения) могут перемещаться по поверхности проводящего тела. Расчеты ёмкости уединенного тела, конденсатора или системы заряженных тел, как правило, значительно упрощаются, если удается «задать» характер распределения электрического заряда по поверхности проводящего тела и использовать принцип суперпозиции для расчета напряженности электростатического поля и далее для расчета разности потенциалов между поверхностями проводящих тел.