Первый и второй законы Кирхгофа в комплексной форме

По аналогии с законом Ома в комплексной форме, применяя метод комплексных амплитуд к сложной электрической цепи, содержащей пассивные и активные элементы, можно сформулировать законы Кирхгофа в комплексной форме, учитывая формулировки эти же законы для мгновенных значений токов и напряжений (см. п. 3.3).

Тогда согласно первому закону Кирхгофа в комплексной форме алгебраическая сумма комплексных амплитуд токов всех ветвей, подключенных к одному и тому же узлу электрической цепи, равна нулю

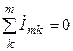, (4.24)

где 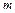— число ветвей, подключенной к узлу; 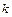— номер ветви, подключенной к узлу; 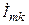— комплексная амплитуда тока k-ой ветви.

Аналогичное уравнение может быть записано для комплексных действующих значений токов ветвей, подключенных к одному и тому же узлу электрической цепи,

,

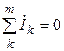где 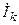— комплексное действующее значение тока k-ой ветви.

Согласно второму закону Кирхгофа в комплексной форме алгебраическая сумма комплексных амплитуд напряжений пассивных элементов и источников тока, входящих в состав контура электрической цепи, равна алгебраической сумме комплексных амплитуд э.д.с. идеальных источников напряжения, действующих в этом контуре,

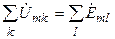, (4.25)

где 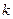— номер ветви контура; 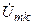— комплексная амплитуда напряжения на k-ом ветви контура; 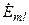— комплексная амплитуда l-ой э.д.с. идеального источника напряжения, действующего в контуре.

Аналогичное уравнение может быть записано, используя комплексные действующие значения напряжений и э.д.с.,

.

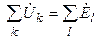где 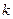— номер ветви контура; 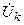— комплексное действующее значение напряжения на k-ой ветви контура; 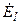— комплексное действующее значение l-ой э.д.с. идеального источника напряжения, действующего в контуре.

Суммирование комплексных амплитуд (комплексных действующих значений) токов и напряжений электрической цепи в выше приведённых формулах выполняется с учётом их направления по тем же правилам, что и суммирование мгновенных значений.