Понятие о методе комплексных амплитуд
Поскольку в реактивных элементах цепи (ёмкости и индуктивности) ток и напряжение связаны интегрально-дифференциальные соотношениями (2.4), (2.5) и (2.10), (2.11), то уравнения электрического равновесия такой будут представлять собой интегрально-дифференциальные уравнения, решение которых во временной области переменной 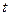 является достаточно трудоемкой задачей.
является достаточно трудоемкой задачей.
Однако, поскольку производная и интеграл по времени любого порядка от гармонической функции представляют собой также гармоническую функцию, то при гармоническом воздействии все напряжения и токи цепи, в установившемся режиме будут также гармоническими функциями времени той же частоты, что и частота воздействия. Поэтому всем этим гармоническим функциям будет соответствовать комплексные изображения, аналогичные функции 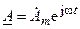 , важным свойством которой является то, что она не изменяет своего вида при многократном дифференцировании и интегрировании по времени. Действительно, производная n-го порядка по времени от функции
, важным свойством которой является то, что она не изменяет своего вида при многократном дифференцировании и интегрировании по времени. Действительно, производная n-го порядка по времени от функции 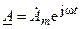 имеют вид
имеют вид 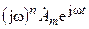 , то есть сводится к умножению исходной функции на
, то есть сводится к умножению исходной функции на 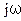 столько раз, каков порядок производной. Последовательное n-кратное интегрирование по времени функции
столько раз, каков порядок производной. Последовательное n-кратное интегрирование по времени функции 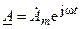 преобразует её к виду
преобразует её к виду 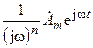 , то есть сводится к делению исходной функции на
, то есть сводится к делению исходной функции на 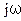 столько раз, каков порядок интеграла.
столько раз, каков порядок интеграла.
Метод комплексных амплитуд заключается в следующем. В интегрально-дифференциальных уравнениях цепи все вещественных гармонические функций напряжений и токов (оригиналы), заменяют изображениям в виде комплексных показательных функций 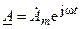 и выполняют операций дифференцирования и интегрирования. В результате все уравнения будут содержать только слагаемые вида
и выполняют операций дифференцирования и интегрирования. В результате все уравнения будут содержать только слагаемые вида 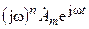 и
и 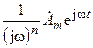 , в состав которых входит сомножитель
, в состав которых входит сомножитель 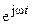 . После сокращения этого сомножителя уравнения преобразуются из интегрально-дифференциальных в алгебраические.
. После сокращения этого сомножителя уравнения преобразуются из интегрально-дифференциальных в алгебраические.
Решая полученных алгебраические уравнения при условии постоянства частоты 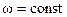 , находят комплексные амплитуды токов и напряжений, зная которые определяют вещественные гармонические функции токов и напряжений путем обратного перехода от изображений к оригиналам.
, находят комплексные амплитуды токов и напряжений, зная которые определяют вещественные гармонические функции токов и напряжений путем обратного перехода от изображений к оригиналам.
Достоинством метода комплексных амплитуд является существенное упрощение расчёта цепи, а недостатком — возможность расчета цепи только при гармоническом воздействии и только в установившемся режиме
4.5. Комплексные сопротивление и проводимость цепи при гармоническом
воздействии
Пусть к цепи, составленной из пассивных идеальных элементов и имеющей два вывода, приложено гармоническое напряжение
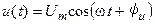 ,
,
где 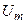 и
и 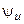 — амплитуда и начальная фаза напряжения.
— амплитуда и начальная фаза напряжения.
Тогда ток такой цепи будет также гармонической функцией времени той же частоты, что и напряжение
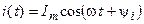 .
.
где  и
и 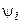 — амплитуда и начальная фаза тока.
— амплитуда и начальная фаза тока.
В соответствии с методом комплексных амплитуд, заменим вещественные функции напряжения 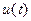 и тока
и тока 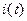 их изображениями в показательной форме записи:
их изображениями в показательной форме записи:
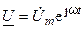 ;
;
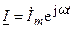 ,
,
где 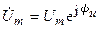 ,
, 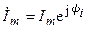 — комплексные амплитуды напряжения и тока.
— комплексные амплитуды напряжения и тока.
Рассмотрим отношение изображений напряжения и тока
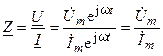 . (4.11)
. (4.11)
Полученная комплексная функция в виде отношения комплексных амплитуд напряжения и тока называется комплексным сопротивлением цепи. Такое название функции обусловлено тем, что уравнение (4.11) по форме записи аналогично закону Ома (2.1).
Подставляя в (4.11) выражения для комплексных амплитуд напряжения и тока в показательной форме, получаем
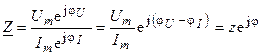 . (4.12)
. (4.12)
где 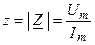 и
и 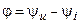 — модуль и аргумент комплексного сопротивления.
— модуль и аргумент комплексного сопротивления.
Из (4.12) следует, что в зависимости от значений начальных фаз напряжением и током аргумент  комплексного сопротивления может быть как положительным, так и отрицательным числом.
комплексного сопротивления может быть как положительным, так и отрицательным числом.
Поделив числитель и знаменатель правой части уравнения (4.12) на 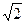 , получим аналогичное выражение для комплексного сопротивления в виде отношения комплексных действующих значений напряжения и тока
, получим аналогичное выражение для комплексного сопротивления в виде отношения комплексных действующих значений напряжения и тока
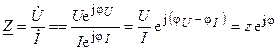 . (4.13)
. (4.13)
где 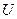 ,
, 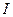 — действующие значения гармонических функций напряжения и тока
— действующие значения гармонических функций напряжения и тока
Примечание. При расчёте электрических цепей комплексные действующие значения напряжения и тока обычно называют просто комплексным напряжением и комплексным током, опуская слово «действующее», что и будет использовано в дальнейшем.
С помощью формулы Эйлера, можно преобразовать показательную форму записи комплексного сопротивления (4.13) в алгебраическую
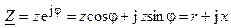 , (4.14)
, (4.14)
где 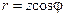 и
и 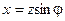 — вещественная (активная) и мнимая (реактивная) составляющие комплексного сопротивлении;
— вещественная (активная) и мнимая (реактивная) составляющие комплексного сопротивлении; 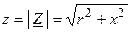 — модуль комплексного сопротивления;
— модуль комплексного сопротивления; 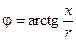 — аргумент комплексного сопротивления.
— аргумент комплексного сопротивления.
Комплексное сопротивление 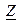 может быть изображено на комплексной плоскости в виде вектора (рис. 4.7, а), проведённого из начала координат в точку с координатами
может быть изображено на комплексной плоскости в виде вектора (рис. 4.7, а), проведённого из начала координат в точку с координатами 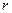 и
и 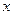 . Длина такого вектора будет равна модулю z, а угол наклона вектора к положительной вещественной полуоси — аргументу j комплексного сопротивления.
. Длина такого вектора будет равна модулю z, а угол наклона вектора к положительной вещественной полуоси — аргументу j комплексного сопротивления.
Величина, обратная комплексному сопротивлению, называется комплексной проводимостью цепи
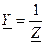 .
.
С учётом (4.11) и (4.13) комплексная проводимость может быть определена в виде
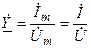 . (4.15)
. (4.15)
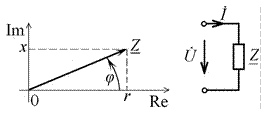
а) б)
Рис. 4.7
Запишем комплексную проводимость в алгебраической и показательной форме
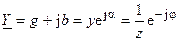 , (4.16)
, (4.16)
где 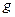 и
и 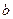 — вещественная (активная) и мнимая (реактивная) составляющие комплексной проводимости соответственно;
— вещественная (активная) и мнимая (реактивная) составляющие комплексной проводимости соответственно; 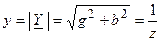 — модуль комплексной проводимости;
— модуль комплексной проводимости; 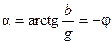 — аргумент комплексной проводимости.
— аргумент комплексной проводимости.
Используя понятие комплексного сопротивления 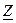 цепи можно рассматриваемую цепь изобразить в виде только одного этого сопротивления (рис. 4.7, б). Полученная за счёт такой замены схема называется комплексной схемой замещения цепи. Аналогичную комплексную схему замещения можно получить, используя комплексной проводимости
цепи можно рассматриваемую цепь изобразить в виде только одного этого сопротивления (рис. 4.7, б). Полученная за счёт такой замены схема называется комплексной схемой замещения цепи. Аналогичную комплексную схему замещения можно получить, используя комплексной проводимости 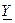 цепи. В обоих случаях токи и напряжения участка цепи будут представлены их комплексными амплитудами или комплексными действующими значениями.
цепи. В обоих случаях токи и напряжения участка цепи будут представлены их комплексными амплитудами или комплексными действующими значениями.
Рассмотрим комплексные сопротивления и проводимости идеализированных элементов электрической цепи.
Дата добавления: 2017-09-01; просмотров: 2861;











