Комплексное изображение гармонической функции

Рассмотрим показательную комплексную функцию времени

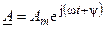, (4.6)

у которой модуль 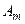и аргумент 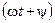совпадают с амплитудой и мгновенной фазой гармонической функции (4.4).

Выделив в (4.5) в виде сомножителя оператор вращения 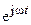, получим

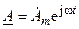, (4.7)

где

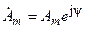, (4.8)

— величина, называемая комплексной амплитудой, в обозначении которой точка над символом широко используется в технической литературе.

Из (4.8) видно, что комплексная амплитуда не зависит от времени, а её модуль 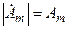и аргумент 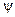равны соответственно амплитуде и начальной фазе гармонической функции (4.4).

Используя формулу Эйлера 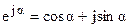, запишем функцию (4.6) в тригонометрической форме

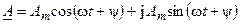, (4.9)

Сравнивая формулы (4.9) и (4.4), видно, что действительная часть (4.9) совпадает с гармонической функцией (4.4). Указанное соответствие записывается в символическом виде следующим образом

,

где « 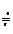» — символом соответствия, который не следует путать со знаком равенства «=».

При этом гармоническую функцию (4.4) называют оригиналом, а комплексную функцию (4.6) — изображением.

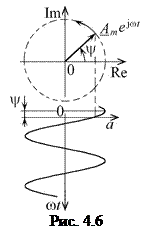
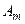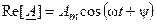На комплексной плоскости функция (4.6) изображается в виде вектора длиной , вращающегося с угловой скоростью вокруг начала координат в направлении против часовой стрелки, которое на векторных диаграммах принимают за положительное изменению мгновенной фазы (рис. 4.6). 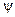Проекция вектора на вещественную ось совпадает с гармонической функцией (4.4), а начальное положение вектора в момент — с начальной фазой этой функции.

В качестве изображения гармонической функции (4.4) наряду с комплексной амплитудой 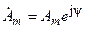используется комплексное действующее значение

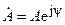, (4.10)

модуль которого равен действующему значению 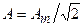, а аргумент y — начальной фазе: гармонической функции.

С учётом (4.5) комплексное действующее значение может быть выражено через комплексную амплитуду

.

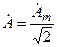Рассмотрим примеры преобразования гармонических функций напряжения и тока в комплексные амплитуды, а также обратного преобразования.

Пример 1 Найти комплексные амплитуды напряжения 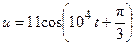В и тока .

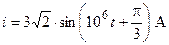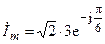Решение: В, А.

Пример 2 Зная комплексные амплитуды напряжения 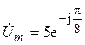В и тока 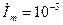, найти соответствующие им гармонические функции.

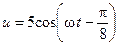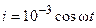Решение: В, А.

Лекция № 5