Омическое сопротивление при гармоническом воздействии

Пусть к сопротивлению приложено напряжение, изменяющееся по гармоническому закону

,

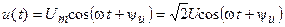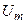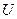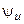где , и — амплитуд, действующее значение и начальные фазы напряжения.

Определим по закону Ома ток идеализированного сопротивления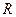

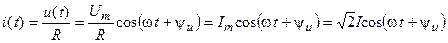. (4.17)

где 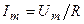, , 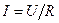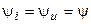— амплитуда, действующее значение и начальная фаза тока.

Из (4.17) следует, что ток сопротивления изменяется по гармоническому закону с той же частотой, что и напряжение. Поскольку начальная фаза тока совпадает с начальной фазой напряжения, то говорят, что ток изменяется синфазно с напряжением. Определи мгновенную мощность сопротивления

.

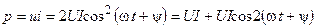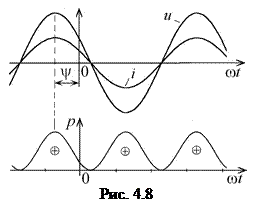Временные диаграммы напряжения, тока и мгновенной мощности показаны на рис. 4.8.

Найдём активную мощность сопротивления, равную среднему значению мощности за период ,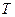

.

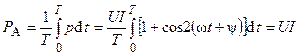Таким образом, мгновенную мощность сопротивления содержит постоянную составляющую 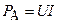и переменную составляющую 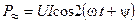с частотой 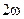, амплитуда которой равна 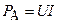. Поэтому мощность, выделяемая в сопротивлении всегда имеет положительное значение.

В соответствии с методом комплексных амплитуд заменим в (4.17) вещественные функции (оригиналы) напряжения 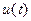и тока 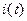их изображениями в показательной форме запис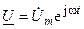и и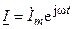

.

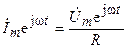Сокращая оператор вращения 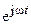, который содержится в обеих частях уравнения в виде сомножителя, и учитывая, что 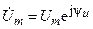, находим комплексную амплитуду тока

.

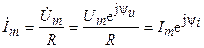где 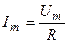и 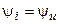— модуль и начальная фаза комплексной амплитуды тока сопротивления.

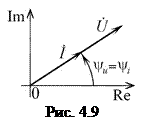
На рис. 4.9 показана векторная диаграмма комплексных напряжения и тока сопротивления. Поскольку аргументы комплексных амплитуд тока и напряжения равны, то, следовательно, гармонические ток изменяются синфазно с напряжением, что совпадает с результатом, полученным ранее для в вещественных функций напряжения и тока.

Найдём комплексное сопротивление идеализированного сопротивления

,

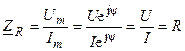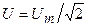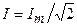где и — действующие значения тока и напряжения сопротивления.

Комплексное сопротивление 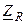может быть записано также в показательной и алгебраической форме

.

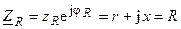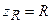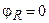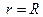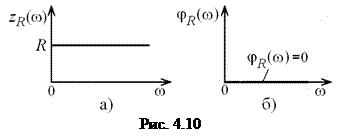
Из последнего уравнения находим модуль , аргумент , а также вещественную и мнимую 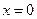составляющие комплексного сопротивления. Таким образом, модуль и аргумент идеализированного сопротивления не зависят от частоты (рис. 4.10).

Определим комплексную проводимость идеализированного сопротивления

.

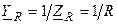На комплексной плоскости комплексные сопротивление 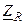(рис. 4.11, а) и проводимость 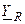(рис. 4.11, б) идеализированного сопротивления изображаются в виде векторов, направленных вдоль вещественной оси. Используя понятие комплексного сопротивления, можно идеализированное сопротивление заменить в электрической схеме комплексной схемой замещения (рис. 4.11, в), которая отличается от схемы (рис. 2.1) только тем, что в ней вещественные напряжения и ток заменены их комплексными действующими значениями.

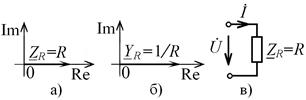
Рис. 4.11