Закон Био-Савара-Лапласа. Ток смещения и закон полного тока.
Допустим, что закон Био-Савара-Лапласа в форме (1) раздела 11.1 справедлив для квазистационарных условий, более общих, чем условия магнитостатики. Ниже будем предполагать, что в рассматриваемом контрольном объёме может происходить изменение во времени электрического заряда. В разделе 10 настоящего пособия описаны условия, при выполнении которых электромагнитные процессы можно рассматривать как квазистационарные. Более полное определение квазистационарных условий будет получено в процессе рассмотрения проблемы. Следствием подобного допущения будет являться естественное заключение о несуществовании в природе магнитных зарядов, т.е. заключение о справедливости соотношений (3) и (5) раздела 11.1 при тех же условиях.
Рассмотрим второе из следствий закона Био-Савара-Лапласа. Вычислим ротор векторного поля магнитной индукции (2) раздела 11.1 в предположении о возможности дифференцирования по параметру под знаком интеграла:
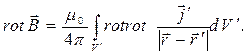
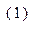
В соответствии с известным тождеством векторного анализа
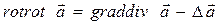 ,
, 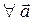 (2)
(2)
преобразуем подынтегральное выражение правой части соотношения (1):
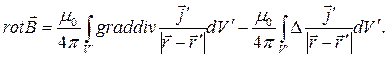
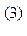
Напомним, что лапласиан во втором интеграле правой части уравнения (3) вычисляется по координатам точки наблюдения (т.е. не штрихованные переменные). Далее используем известное из математической физики соотношение
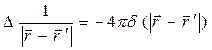
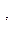
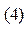
основное свойство дельта-функции Дирака
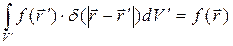
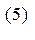
и получаем промежуточный результат:
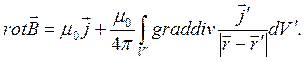
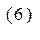
Подынтегральное выражение в соотношении (6) в соответствии с его определением можно вычислить, используя дифференциальные операции по не штрихованным переменным, но получающийся при этом результат не отличается очевидным физическим смыслом. В рассматриваемом случае при вычислении дивергенции вектора в подынтегральном выражении целесообразно от дифференциальных операций по координатам точек наблюдения (не штрихованные переменные) перейти к диффренциальным операциям по координатам точек расположения элементарных объёмов с определённой плотностью тока (штрихованные переменные). С этой целью рассмотрим тождество:
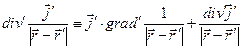 ,
,
в котором все дифференциальные операции выполняются по штрихованным переменным. Вычислим результат операции 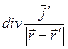 с учётом того, что
с учётом того, что 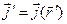 :
:
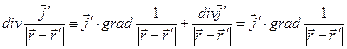 .
.
Заметим, что имеет место соотношение
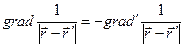 .
.
С учётом всего перечисленного можно записать необходимое для дальнейшего вывода соотношение
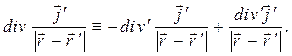
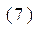
Переход к дифференцированию по координатам точек расположения элементов объёма с током позволяет воспользоваться дифференциальной формой закона сохранения электрического заряда (напомним, что закон сохранения электрического заряда установлен задолго до открытия закона полного тока):
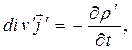
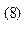
где 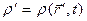 - объёмная плотность электрического заряда, и получить в результате:
- объёмная плотность электрического заряда, и получить в результате:
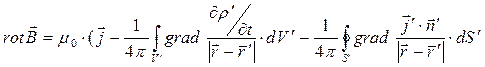 ). (9)
). (9)
При записи соотношения (9) использована теорема Остроградского-Гаусса и один из интегралов по объёму преобразован в интеграл по замкнутой поверхности, ограничивающей контрольный объём. Вычисление градиента подынтегральных выражений в уравнении (9) производится по координатам точек наблюдения.
В условиях магнитостатики первый интеграл в круглых скобках уравнения (9) равен нулю, в квазистационарных условиях 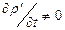 . Заметим, что имеет место соотношение:
. Заметим, что имеет место соотношение:
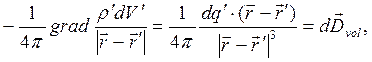
 (10)
(10)
где 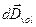 - дифференциал вектора
- дифференциал вектора 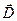 в точке наблюдения, образованный элементарным объёмным зарядом
в точке наблюдения, образованный элементарным объёмным зарядом 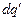 , расположенным в точке пространства с радиус-вектором
, расположенным в точке пространства с радиус-вектором 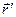 . В условиях электростатики проведенные выкладки сомнению не подлежат. В квазистационарных условиях предполагаем, что для каждого момента времени
. В условиях электростатики проведенные выкладки сомнению не подлежат. В квазистационарных условиях предполагаем, что для каждого момента времени 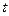 справедливы уравнения
справедливы уравнения
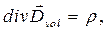
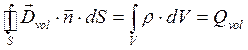 , (11)
, (11)
что эквивалентно использованию теоремы Гаусса для вектора 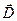 с учётом распределения электрического заряда по объёму
с учётом распределения электрического заряда по объёму 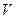 (следствие закона Кулона и определения вектора поляризованности среды). Если согласиться с полученным выше результатом, имеем:
(следствие закона Кулона и определения вектора поляризованности среды). Если согласиться с полученным выше результатом, имеем:
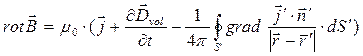 . (12)
. (12)
Остаётся обсудить интеграл по замкнутой контрольной поверхности. Если в каждой точке замкнутой контрольной поверхности выполнено условие 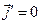 , то рассматриваемый интеграл не даёт вклада в правую часть уравнения (12). Если имеют место условия
, то рассматриваемый интеграл не даёт вклада в правую часть уравнения (12). Если имеют место условия 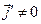 , но
, но 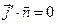 в каждой точке контрольной поверхности, то получаем аналогичный результат. В общем случае допустим, что на контрольной поверхности имеет место закон сохранения электрического заряда в форме
в каждой точке контрольной поверхности, то получаем аналогичный результат. В общем случае допустим, что на контрольной поверхности имеет место закон сохранения электрического заряда в форме
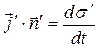 .
. 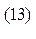
Физический смысл соотношения (13) требует уточнения. Производная в правой части соотношениея (13) описывает скорость изменения поверхностной плотности электрического заряда на контрольной поверхности, обусловленную только токами, вытекающими из контрольного объёма.
Воспользуемся цепочкой преобразований
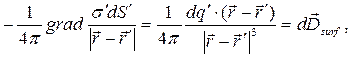
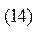
где 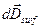 - дифференциал вектора
- дифференциал вектора 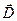 в точке наблюдения, образованный элементарным поверхностным зарядом
в точке наблюдения, образованный элементарным поверхностным зарядом 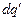 , расположенным в точке замкнутой контрольной поверхности с радиус-вектором
, расположенным в точке замкнутой контрольной поверхности с радиус-вектором 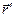 . С учетом выражения (14) после вычисления интеграла в правой части уравнения (12) получаем окончательный результат в дифференциальной форме:
. С учетом выражения (14) после вычисления интеграла в правой части уравнения (12) получаем окончательный результат в дифференциальной форме:
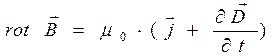
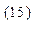
В уравнении (15) вектор 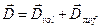 обусловлен наличием как зарядов, распределённых по контрольному объёму, так и распределённых по контрольной поверхности, т.е. это вектор
обусловлен наличием как зарядов, распределённых по контрольному объёму, так и распределённых по контрольной поверхности, т.е. это вектор 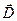 результирующего электрического поля. Принципиальным результатом соотношений (15) и (16) является возможность генерировать магнитное поле не только электрическим током проводимости, но и переменным во времени электрическим полем. Магнитное поле возникает как результат совокупного воздействия первого и второго фактора.
результирующего электрического поля. Принципиальным результатом соотношений (15) и (16) является возможность генерировать магнитное поле не только электрическим током проводимости, но и переменным во времени электрическим полем. Магнитное поле возникает как результат совокупного воздействия первого и второго фактора.
Для вектора напряжённости магнитного поля из уравнения (15) и определения силы тока
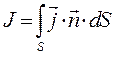
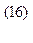
получаем
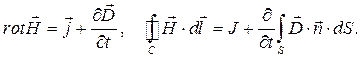 (17)
(17)
Использованное выше предположение, что на контрольной поверхности может накапливаться поверхностная плотность электрического заряда, не должно вызывать возражений, даже если контрольная поверхность проведена так, что нормальная составляющая объёмной плотности тока не терпит разрыва. Если рассматриваемую контрольную поверхность окружить ещё большей замкнутой поверхностью, то для второго (дополнительного) объёма внешняя нормаль будет противоположна по направлению внешней нормали к исходной поверхности и суммарный эффект накопления поверхностных зарядов не будет проявляться в форме записи уравнения (15) для составного объёма. Приведенное рассуждение согласуется с принципом суперпозиции, позволяя рассматривать векторое поле с источниками поля, расположенными в разных областях пространства.
Строгий анализ возможности применения уравнений электро- и магнитостатики в квазистационарных условиях на основе системы уравнений Максвелла (с ней мы познакомимся в следующей главе) показывает, что приведённый вывод сохраняет силу, если характерное время динамической системы значительно больше времени распространения электромагнитного сигнала по рассматриваемой области. Этот анализ выходит за рамки настоящего учебного пособия.
Выкладки настоящего раздела, к сожалению, не отличаются простотой. Помимо предположения, что закон Био-Савара-Лапласа справедлив в квазистационарных условиях, нам пришлось использовать закон сохранения электрического заряда и теорему Гаусса для вектора 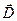 (аналогично тому, как это было использовано в предыдущем разделе) и привлечь математические результаты теории поля (векторный анализ). Остаётся вопрос, зачем проделан этот анализ? Ответом на этот вопрос служит выявление того факта, что
(аналогично тому, как это было использовано в предыдущем разделе) и привлечь математические результаты теории поля (векторный анализ). Остаётся вопрос, зачем проделан этот анализ? Ответом на этот вопрос служит выявление того факта, что
закон Кулона, теорема Гаусса для вектора 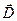 , закон сохранения электрического заряда и закон Био-Савара-Лапласа являются не разрозненными, независимыми друг от друга закономерностями, а образуют внутренне непротиворечивую систему закономерностей электромагнитного поля.
, закон сохранения электрического заряда и закон Био-Савара-Лапласа являются не разрозненными, независимыми друг от друга закономерностями, а образуют внутренне непротиворечивую систему закономерностей электромагнитного поля.
Рассмотрим один поучительный пример важности практического учёта существования тока смещения.
Металлическая сфера с электрическим зарядом 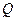 помещена в однородную изотропную слабо проводящую среду с известными диэлектрическими свойствами. Электрический заряд сферы медленно уменьшается с течением времени. Определить напряжённость магнитного поля в окружающем пространстве.
помещена в однородную изотропную слабо проводящую среду с известными диэлектрическими свойствами. Электрический заряд сферы медленно уменьшается с течением времени. Определить напряжённость магнитного поля в окружающем пространстве.
Предположим, что параметры среды, в которую помещена сфера, таковы, что выполняются условия квазистационарности процесса разрядки сферы. В этом случае для решения задачи можно использовать уравнения закона полного тока в дифференциальной или интегральной форме (17) вместе с предположением о справедливости статических закономерностей при определении вектора 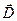 и объёмной плотности тока проводимости
и объёмной плотности тока проводимости 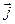 . Если начало сферической системы координат поместить в центр сферы, задача будет обладать сферической симметрией: все физические величины не должны зависеть от угловых переменных. Для мгновенного распределения объёмной плотности тока проводимости справедливы зависимости
. Если начало сферической системы координат поместить в центр сферы, задача будет обладать сферической симметрией: все физические величины не должны зависеть от угловых переменных. Для мгновенного распределения объёмной плотности тока проводимости справедливы зависимости
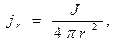
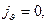
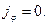 (18)
(18)
Здесь J - электрический ток разрядки сферы (ток проводимости). Для мгновенного распределения составляющих вектора 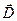 имеем
имеем
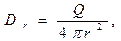
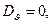
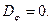 (19)
(19)
Изменение величины 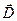 с течением времени в фиксированной точке пространства в условиях квазистационарности приводит к соотношениям:
с течением времени в фиксированной точке пространства в условиях квазистационарности приводит к соотношениям:
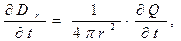
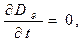
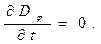 (20)
(20)
Из закона сохранения электрического заряда при разрядке сферы следует уравнение:
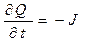 . (21)
. (21)
В итоге оказывается, что в пространстве вне металлической сферы объёмная плотность полного тока обращается в нуль:
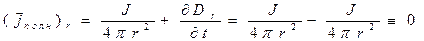 .
.
В соответствии с уравнением (17) ротор вектора напряжённости магнитного поля должен быть равен нулю:
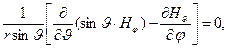 (22)
(22)
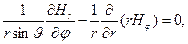 (23)
(23)
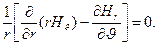 (24)
(24)
Вспомним, что все частные производные по угловым переменным от составляющих вектора напряжённости магнитного поля должны обращаться в нуль (условие сферической симметрии рассматриваемой задачи). Из уравнения (22) в этом случае следует
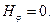 (25)
(25)
Уравнение (23) при этом удовлетворяется автоматически, а из уравнения (23) следует, что
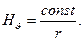 (26)
(26)
Из уравнения
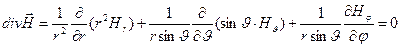 , (27)
, (27)
которое справедливо, если материальная среда однородная и изотропная, можно получить
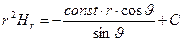 . (28)
. (28)
Поскольку левая часть соотношения (28) не зависит от угловой координаты, величину const необходимо положить равной нулю. Постоянную интегрирования С также следует положить равной нулю, поскольку радиальный ток не может создать радиальное магнитное поле: в силу закона Био-Савара-Лапласа силовые линии магнитного поля ортогональны силовым линиям объёмной плотности тока. В итоге получаем, что в пространстве вне металлической сферы магнитное поле отсутствует.
С использованием закона полного тока в интегральной форме (17) решение задачи сводится к следующему. Запишем соотношения (18) и (19) в векторном виде:
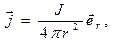
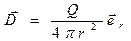 . (29)
. (29)
В пространстве вне сферы рассмотрим произвольный замкнутый контур 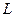 и натянем на него произвольную поверхность S. Поскольку электрический ток, проходящий через рассматриваемую поверхность, является потоком вектора объёмной плотности тока через эту поверхность, перепишем уравнение (17) в форме:
и натянем на него произвольную поверхность S. Поскольку электрический ток, проходящий через рассматриваемую поверхность, является потоком вектора объёмной плотности тока через эту поверхность, перепишем уравнение (17) в форме:
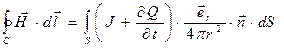 . (30)
. (30)
При записи соотношения (30) учтено, что рассматриваемый контур С и поверхность S не изменяются с течением времени. Привлекая уравнение (21), заключаем, что левая часть уравнения (30) равна нулю. Поскольку полученный результат справедлив для произвольного контура, из него следует, что в пространстве вне сферы магнитное поле отсутствует.
Что же получено в результате? В пространстве имеет место ток проводимости, а магнитное поле отсутствует. Этот результат невозможно объяснить, не привлекая понятия «ток смещения» (или понятия «полный ток»). Только благодаря тому, что полный ток складывается из тока проводимости и тока смещения, только благодаря тому, что в рассматриваемом случае ток проводимости и ток смещения равны по величине и имеют разные знаки, полный ток обращается в нуль, и только поэтому в пространстве вне сферы не возникает магнитное поле.
Дата добавления: 2017-09-01; просмотров: 2282;











