Закон сохранения электрического заряда. Ток смещения и закон полного тока.

Закон сохранения электрического заряда установлен американским физиком и общественным деятелем Бенджамином Франклином (1706-1790) в 1750 году. Согласно этому закону электрический заряд не может возникать или исчезать, его изменение в контролируемом объёме может происходить только в результате перетекания электрического заряда из пространства, окружающего выделенный объём.

Локальная (дифференциальная) формулировка законов сохранения в классической физике сводится к тому, частная производная по времени от объёмной плотности «сохраняемой» величины равна сумме дивергенции плотности потока этой величины, взятой со знаком минус, и мощности «источника» этой величины, рассчитанной на единицу объёма. Закон сохранения электрического заряда, следовательно, должен иметь «дивергентную форму»:

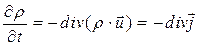. (1)

Здесь 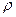- объёмная плотность электрического заряда, 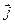- вектор объёмной плотности элетричекого тока, 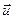- вектор средней скорости направленного движения электрического заряда, 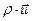- плотность потока электрического заряда. Соотношением

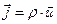(2)

устанавливается физический смысл рассматриваемых величин.

Содержание закона сохранения электрического заряда сводится к утверждению, что объёмная плотность мощности источника электрического заряда тождественно равна нулю.

Заметим, что в условиях магнитостатики закон сохранения электрического заряда сводится к уравнению:

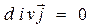(3)

для внутренних точек рассматриваемого объёма. На произвольной поверхности должны быть непрерывны нормальные компоненты вектора объёмной плотности электрического тока:

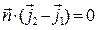. (4)

Для рассматриваемого объёма в целом должно выполняться условие:

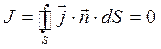. (5)

В качестве первого постулата используем уравнение

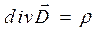. (6)

Вспомним, что уравнение (6) в электростатике являлось следствием закона Кулона, теоремы Гаусса для вектора напряжённости 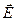электростатического поля и определения физической величины 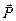поляризованности среды. Утверждение, что уравнение (6) справедливо для случая переменного во времени электромагнитного поля, - это действительно новый постулат. Ниже мы увидим, что уравнение (6) именно с этим физическим содержанием является одним из уравнений системы уравнений классической электродинамики.

Используем уравнение (6) в уравнении (1) - закона сохранения электрического заряда

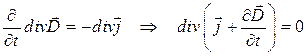. (7)

Поскольку 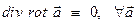, из полученного результата (7) можно заключить:

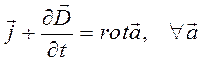. (8)

Но в условиях магнитостатики из закона Био-Савара-Лапласа следует

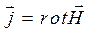. (9)

В качестве второго постулата принимаем утверждение, что уравнение (8) должно переходить в уравнение (9) в случае стационарного электромагнитного поля. Фактически физический смысл второго постулата сводится к утверждению

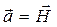. (10)

Итогом наших рассуждений является дифференциальная форма закона полного тока:

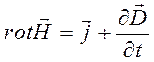. (11)

В правой части уравнения (11) первое слагаемое – 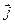- объёмная плотность тока проводимости, второе слагаемое тоже должно быть объёмной плотностью тока, но это не обычный ток проводимости. Величину 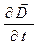называют объёмной плотность тока «смещения»: величина 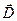связана с поляризованностью 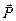среды, изменение которой во времени в свою очередь связано с изменение положения связанных зарядов. Перемещение связанных электрических зарядов в пространстве (даже ограниченное) можно рассматривать как специфический электрический ток:

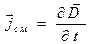. (12)

Сумма объёмной плотности тока проводимости и объёмной плотности тока смещения составляет объёмную плотность полного тока:

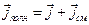. (13)

Таким образом, закон полного тока (11) можно переписать в форме:

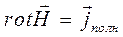. (14)

Закон полного тока в форме (11) или в форме (14) – одно из уравнений системы уравнений Максвелла, система уравнений Максвелла – основа классической электродинамики. Конечно, интересно выяснить степень обоснованности рассмотренного вывода – этот вопрос будет обсуждаться ниже. Специальный раздел пособия будет посвящён интегральной форме закона полного тока (теорема о циркуляции вектора напряжённости магнитного поля).