Опять о теории ССН на примере анализа ЗУР

Рассмотрим построение системы СН на примере зенитной управляемой ракеты (ЗУР).

Рисунок 1 - ЗУР 48Н6Е3

Для рассмотрения принципа работы систем управления и оценки их качества пользуются функциональными и структурными схемами.
Функциональной схемой системы управления называют такую, которая позволяет установить взаимосвязь (функциональную связь) между ее элементами, дает возможность качественно оценить взаимодействие элементов системы и в дальнейшем составить ее структурную схему.
В состав функциональной схемы входят аппаратурные звенья (устройства, обеспечивающие измерение параметра рассогласования, устройства формирования и передачи команд управления, автопилот, органы управления полетом ракеты). Составной частью системы управления является система стабилизации ракеты.
Структурная схема системы управления характеризует динамические связи между различными звеньями, входящими в систему управления, причем все звенья, входящие в систему управления, представляются передаточными функциями, устанавливающими связь выходной величины с входной для каждого звена. При этом в структурную схему включаются и кинематические звенья (их передаточные функции), описывающие динамику перемещения центра масс цели и ракеты в пространстве.
Введение в состав структурной схемы кинематических звеньев позволяет получить замкнутую систему. Структурную схему замкнутой системы управления называют контуром управления.Анализ контура управления характеризует состояние замкнутой системы управления (вспомните материал дисциплины «Радиоавтоматика»). Показатели его качества определяют: устойчивость управления, качество переходных процессов на всех этапах управления полетом ракеты и точность, наведения ракеты на цель.

Рассматривая понятие устойчивости применительно к контуру управления полетом ракеты, можно утверждать, что устойчивый контур управления должен обеспечивать движение ракеты по кинематической траектории при воздействии на его входе регулярных и случайных воздействий, т. е. система управления должна быть с затухающим переходным процессом.
Устойчивость контура управления можно, например, определить по частотным характеристикам разомкнутого контура рассматриваемой системы.

Система автоматического управления должна иметь определенные запасы устойчивости по амплитуде (модулю) и по фазе. Запас устойчивости по амплитуде (модулю) определяется как взятое с обратным знаком значение ординаты логарифмической амплитудно-частотной характеристики при значении фазо-частотной характеристики минус 180°. Запас устойчивости по амплитуде показывает, на сколько децибел можно максимально увеличить коэффициент усиления данной системы в логарифмическом масштабе 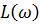, чтобы она не вышла за границы устойчивости. Запас устойчивости по фазе определяется как разность между 180° и абсолютным значением ординаты логарифмической фазочастотной характеристики на частоте среза 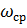. В автоматических системах рекомендуется выбирать запас устойчивости по амплитуде не менее 10—20 дБ, а по фазе — не менее 30—40°. Это условие должно выполняться на этапе наведения ракеты в область встречи с целью.
На последнем этапе наведения ракеты возможен участок неустойчивой работы контура управления. Следует отметить, что в этом случае ошибки наведения ракеты не должны быть выше допустимого значения. Однако, если контур имеет необходимые запасы устойчивости, это еще не означает, что он удовлетворяет поставленным требованиям, так как могут не выполняться условия по быстродействию и точности наведения.

Вспомним критерий устойчивости Найквиста.

АнализустойчивостипоЛЧХ (по критерию Найквиста). Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой системы. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.

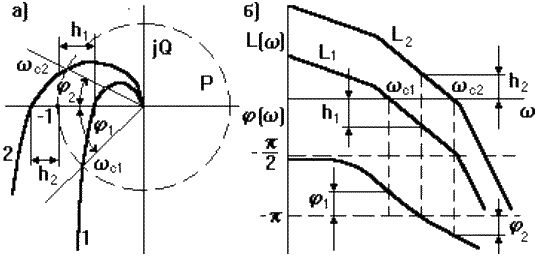
Рисунок 2 – АФЧХ, ЛФЧХ и ЛАЧХ

Пусть известны частотные характеристики двух разомкнутых систем (1 и 2), отличающихся друг от друга только коэффициентом передачи K₁ < K₂. Пусть первая система устойчива в замкнутом состоянии, вторая нет (рис. 2).

Если W₁(p) - передаточная функция первой системы, то передаточная функция второй системы W₂(p) = K 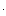W₁(p), где K = K₂/K₁. Вторую систему можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (Безинерционное звено) и W₁(p), поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев. Поэтому ЛАЧХ второй системы: L₂(w) = 20 lg K + L₁(w), а ЛФЧХ: j₂(w) = j₁(w).
Пересечениям АФЧХ вещественной оси соответствует значение фазы j = -p. Это соответствует точке пересечения ЛФЧХ j = -p линии координатной сетки. При этом, как видно на АФЧХ, амплитуды A₁(w) < 1, A₂(w) > 1, что соответствует на ЛАЧХ значениям L₁(w) = 20 lg A₁(w) < 0 и L₂(w) > 0.
Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет устойчива, если значению ЛФЧХ j = -p будут соответствовать отрицательные значения ЛАЧХ и наоборот. Запасам устойчивости по модулю h₁ и h₂, определенным по АФЧХ соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где j = -p, но в логарифмическом масштабе.
Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты w_c1 и w_c2, при которых это происходит, называют частотами среза.
В точках пересечения A(w) = 1 = > L(w) = 0 - ЛАЧХ пересекает горизонтальную ось. Если при частоте среза фаза АФЧХ j_c1 > -p (рис. 2,а кривая 1), то замкнутая система устойчива. На рис. 2 это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка ЛФЧХ, расположенная выше линии j = -p. И, наоборот, для неустойчивой замкнутой системы (рис. 2, а кривая 2) j_c2 < -p, поэтому при w = w_c2 ЛФЧХ проходит ниже линии j = -p. Угол j₁ = j_c1-(-p) является запасом устойчивости по фазе. Этот угол соответствует расстоянию от линии j = -p до ЛФЧХ.
Исходя из сказанного, критерий устойчивости Найквиста по логарифмическим ЧХ, в случаях, когда АФЧХ только один раз пересекает отрезок вещественной оси [-∞; -1], можно сформулировать так: для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию j = -p, была больше частоты среза. Если АФЧХ разомкнутой системы имеет сложный вид, то ЛФЧХ может несколько раз пересекать линию j = -p. В этом случае применение критерия Найквиста несколько усложняется. Однако во многих случаях данной формулировки критерия Найквиста оказывается достаточно.

Пример. На участке 0 ... w _c ФЧХ пересекает линию - 180° один раз. При этом на частоте среза /Y (w _c)/ > 180° . Следовательно, система неустойчива.

Устойчивость контура управления является необходимым, но недостаточным условием его функционирования, поэтому вместе с устойчивостью следует рассматривать качество переходного процесса и точность наведения ЗУР на всех этапах ее полета.

Характеристики переходного процесса определяют способность контура быстро отслеживать изменения входных воздействий, т. е. его динамические свойства.
От качества переходного процесса зависит время вывода ракеты на кинематическую траекторию. Показатель качества определяется временем отработки начального рассогласования, временем и точностью отработки контуром управления маневра цели, возмущений, вызванных изменением способа сопровождения цели и метода наведения ракеты на цель, и т. д.
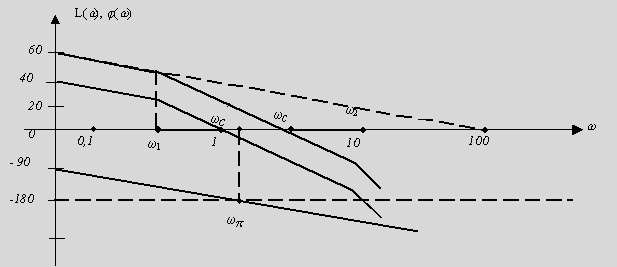
О качестве контура управления в переходном режиме судят по его функционированию при единичном ступенчатом воздействии (рис. 3).

Контур управления отрабатывает это воздействие с некоторой ошибкой, которая, если предположить, что входное воздействие не имеет случайных помех и инструментальных ошибок, получила название динамической.

Динамическая точность системы обеспечивается такими ее свойствами как быстродействие и демпфирование (малая колебательность).

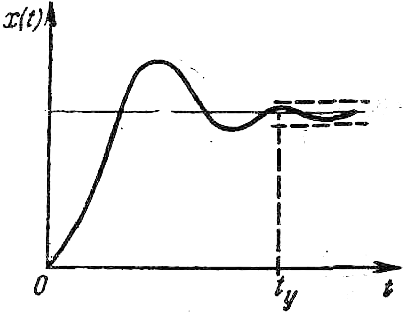
Рисунок 3 – Кривая переходного процесса

Резкие изменения входного сигнала, вызывающие переходный процесс, могут быть следствием маневра цели, помех, изменения способа сопровождения цели, перехода с одного метода наведения на другой и т. д.
В первых трех случаях качество переходного процесса рассматривается в основном с точки зрения величины переходных ошибок, так как встреча ракеты с целью может произойти в любой момент этого процесса. В последнем случае длительность переходного процесса определяет участок траектории, на котором встреча ракеты с целью не произойдет. Переход с одного метода наведения на другой допустим только при достаточном для окончания переходного процесса полетном времени ракеты до точки встречи.
Качество переходного процесса также определяет время отработки начального рассогласования (время вывода ракеты на кинематическую траекторию).

При воздействии на контур медленно изменяющегося управляющего воздействия динамические ошибки в установившемся режиме определяются по формуле

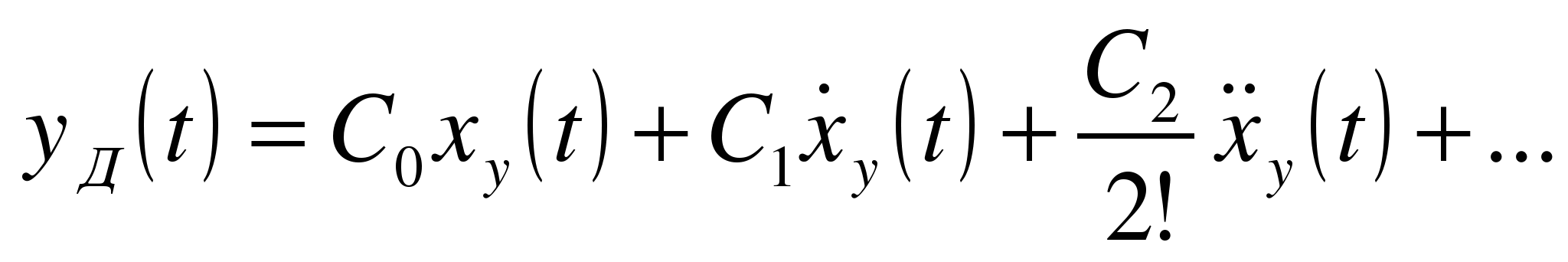, где

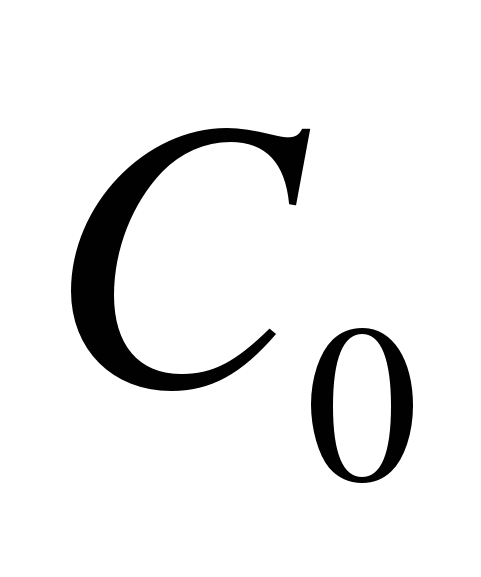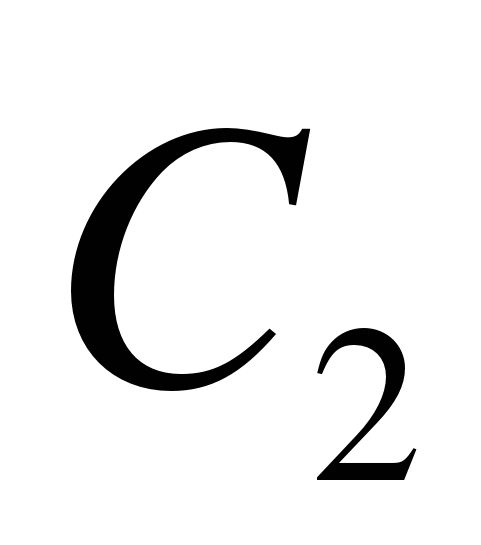, , — коэффициенты динамической ошибки, определяемые по передаточной функции разомкнутого контура управления .

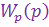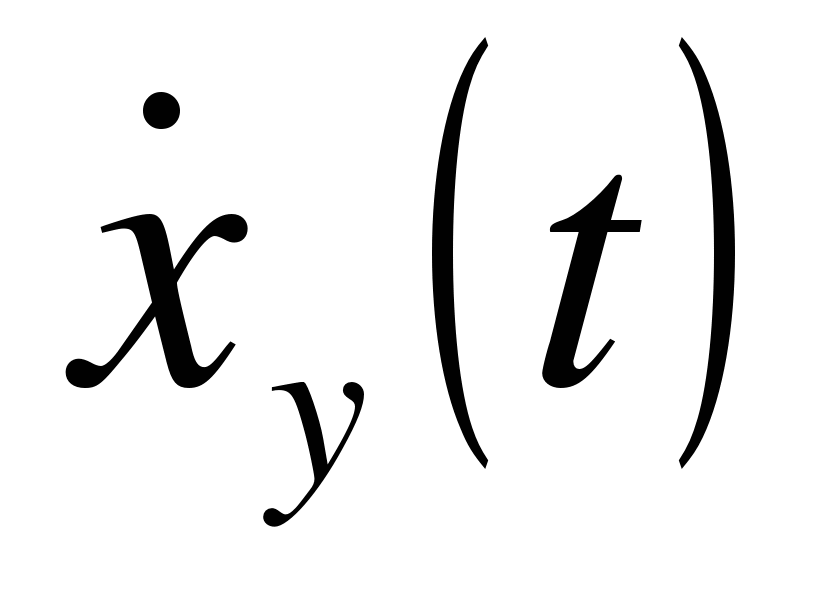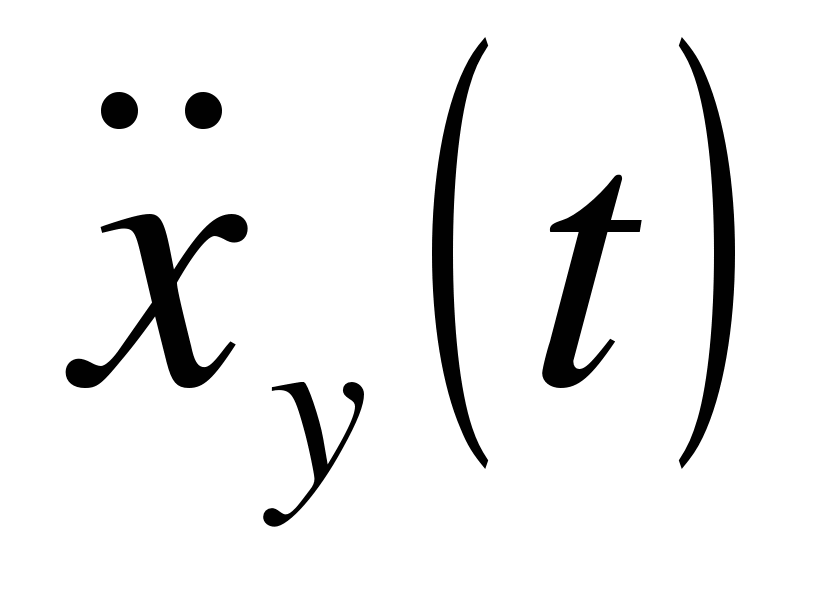, — соответствующие производные управляющего воздействия.
Передаточная функция контура (звена) 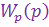— это отношение преобразованных в операторную форму выходной величины y(t) к входной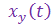

.

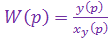В преобразованных функциях вместо времени t независимой переменной подставляют оператор р, который можно считать символом .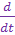
Чтобы найти величину у(t) при известных входной величине 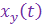и передаточной функции звена (контура), необходимо в операторной форме представить входную величину 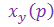,пользуясь специальными таблицами преобразований Лапласа , в которых отражается соответствие величин 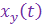и 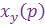, затем определить 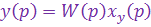и перейти от y(р) к y(t). Вспомним также, что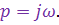

В статических системах управления (системах, не содержащих интегрирующих звеньев) степень астатизма s=0 в установившемся режиме передаточная функция запишется какбезразмерный коэффициент усиления 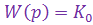, а установившаяся ошибка системы

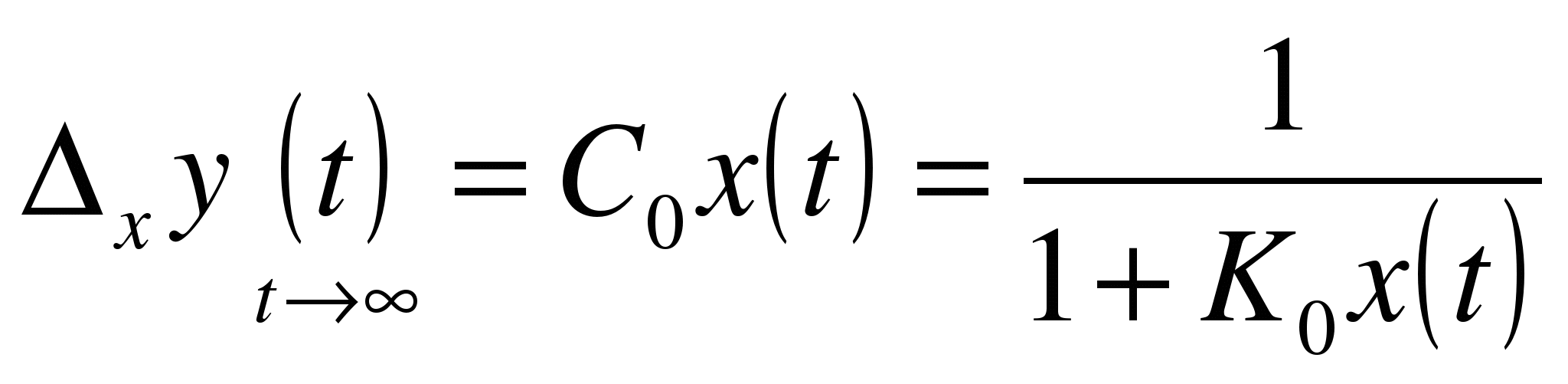
В астатических системах степень астатизма 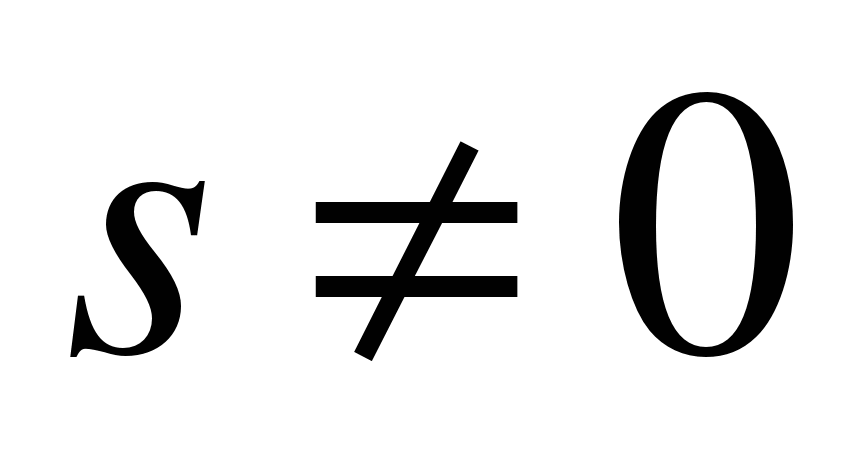. Если s=l, то 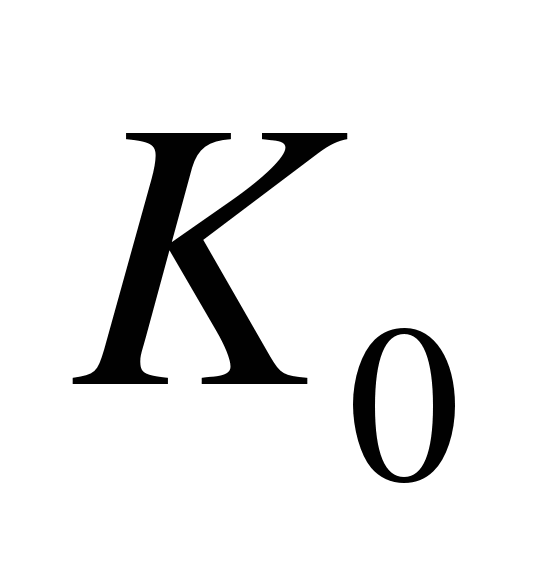имеет размерность 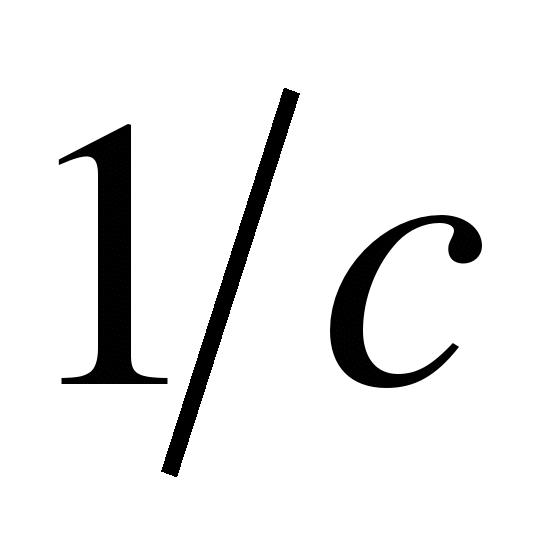и называется коэффициентом усиления (добротностью) системы по скорости. Если s=2, то 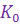имеет размерность 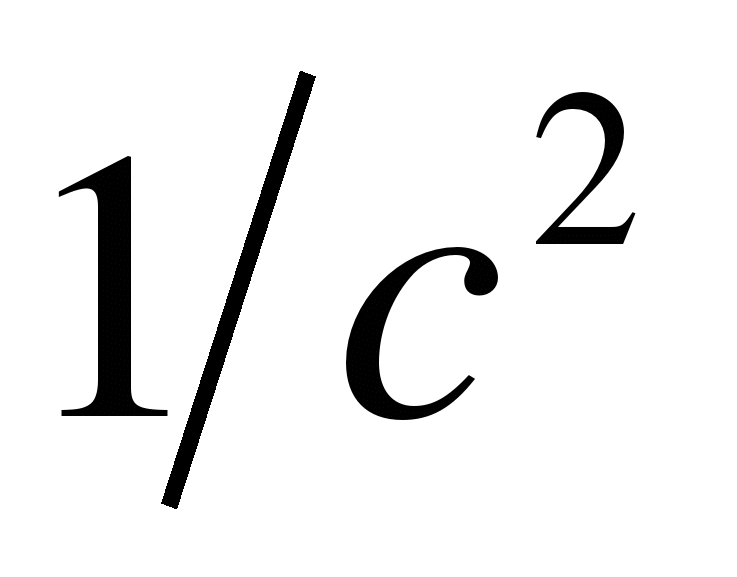и называется коэффициентом усиления (добротностью) системы по ускорению. Оператор ошибки

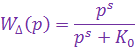
Следовательно, установившаяся ошибка астатической системы s-го порядка пропорциональна s-й производной входного воздействия:

.

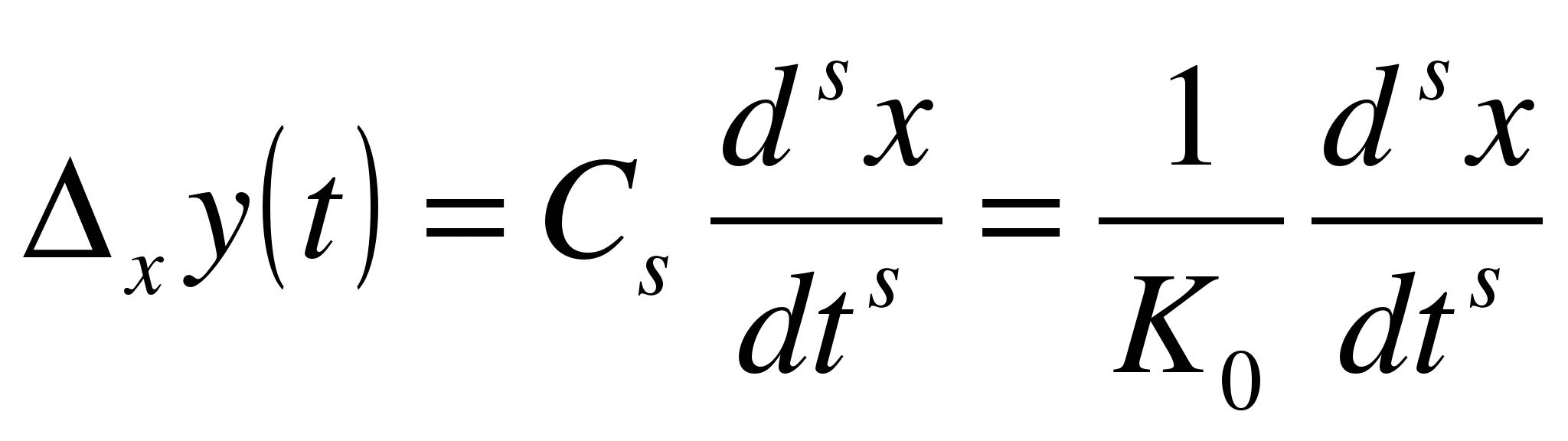Вместе с этим на контур действуют случайные возмущения, обусловливающие флюктуационные ошибки, которые характеризуют отклонение ракеты от динамической траектории.
Причинами возникновения случайных возмущений являются колебания амплитуды и эффективного центра отраженного от цели сигнала, внутренние шумы радиоэлектронной аппаратуры, естественные и искусственные помехи и т. д.
Величина ошибок воспроизведения может быть найдена, если известны передаточная функция контура управления и характеристики управляющего воздействия и помех, действующих на контур управления.
При воздействии на контур случайных процессов ошибка системы все время меняется. Установившееся значение ошибки как таковое отсутствует, поэто­му определяют не саму случайною ошибку 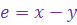, а величину среднеквадратической погреш­ности и однозначно с ней связанную величину дисперсии ошибки воспроизведения .

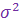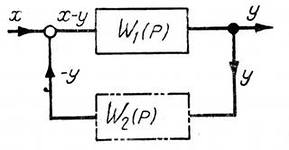
Рисунок 4 – Замкнутая схема CУ с отрицательной обратной связью

Если поступающие на вход контура сигнал 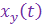и помеха 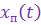взаимно не коррелированы, то для определения величины дисперсии ошибки 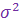требуется знать спектральную плотность сигнала управления 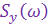, помехи 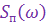и частотную характеристику замкнутого контура управления полетом ракеты 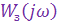, т. е.

.

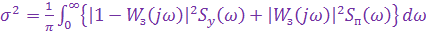В свою очередь

,

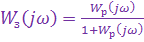где 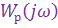— амплитудно-частотная характеристика разомкнутого контура управления.

Для схемы на рис.4 .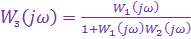

Чтобы иметь представление о том, насколько контур управления полетом ракеты удовлетворяет требованиям по устойчивости, качеству переходного процесса и точности наведения ракеты (при известных сигналах управления и помехи), необходимо знать передаточные функции контура управления и его амплитудно-частотные характеристики.
Для получения аналитического выражения передаточной функции контура управления необходимо располагать математическим описанием физических звеньев, входящих в контур управления, и связями между ними.

Для построения структурных схем необходимо иметь также математическое описание процесса управления ЗУР, выражаемое системой уравнений. Работа контура управления полетом ракеты в общем случае описывается системой нелинейных дифференциальных уравнений.

Вид этих уравнений определяется типом системы управления.

Для систем самонаведения эти уравнения характеризуют относительную скорость перемещения центров масс ракеты и цели в направлении вектора дальности (ракета — цель) и по нормали к нему.

Для командной системы телеуправления и системы управления по лучу кинематические уравнения устанавливают связь относительных скоростей сближения ракеты и цели.

При анализе контура управления, как правило, рассматривают две независимые системы, управляющие движением ракеты в двух независимых взаимно перпендикулярных плоскостях.
Точность наведения ракеты на цель зависит от параметров движения цели, характеристик и инструментальной точности работы звеньев, входящих в состав контура управления, и возникающих внутри контура паразитных возмущений. Она может быть определена путем решения полной системы дифференциальных уравнений с переменными коэффициентами, описывающих поведение системы управления при входном воздействии, имеющем регулярную и случайную составляющие.

В инженерной практике находят применение приближенные методы анализа системы управления при следующих допущениях: неустановившееся возмущенное движение ракеты отличается от исходного установившегося лишь малым отклонением параметров движения, что позволяет свести нелинейные дифференциальные уравнения к линейным; «замораживаются» переменные коэффициенты дифференциальных уравнений системы управления.

Введение допущений позволяет для оценки качества функционирования контура управления полетом ракеты применять метод передаточных функций или частотный метод.

В состав контура самонаведения ЗУР входят головка самонаведения, зенитная управляемая ракета с системой стабилизации и кинематическое звено (КЗ-2). Система самонаведения помимо контура, замыкающегося через кинематическое звено, имеет ряд внутренних контуров автоматического управления.

Движение цели, а также продольное движение ракеты определяют внешние регулярные возмущения контура.
Для реализации методов самонаведения необходима информация об угловой скорости линии визирования цели (методы пропорционального и параллельного сближения) или текущем значении угла упреждения (методы погони). Формирование команд управления, как правило, осуществляется с учетом различного рода компенсационных поправок. В этом случае возникает необходимость в получении информации как об угловых скоростях линии ракета — цель, так и о величине углов упреждения (пеленга) цели.

Решение задачи автоматического слежения за целью головкой самонаведения, размещенной на борту ракеты, осуществляется координатором с помощью различных следящих приводов. В системах самонаведения ракет наибольшее применение нашли так называемые подвижные координаторы.
Они обеспечивают перемещение равносигнального направления относительно корпуса ракеты независимо от его движения. Поворот равносигнальной линии может производиться либо механически (поворотом антенны), либо электрически (при использовании ФАР и др.).

Антенна и исполнительное устройство подвижного координатора развязываются относительно угловых движений корпуса ракеты. Эта развязка достигается использованием в координаторе гироплатформ и гироскопических исполнительных устройств.
Ошибки сопровождения цели должны быть минимальными, даже при небольших дальностях ракета — цель, когда скорость сопровождения велика.

Антенна жестко установлена на гиростабилизированной платформе. Ее разворот в направлении на цель достигается соответствующим разворотом гиро­платформы.

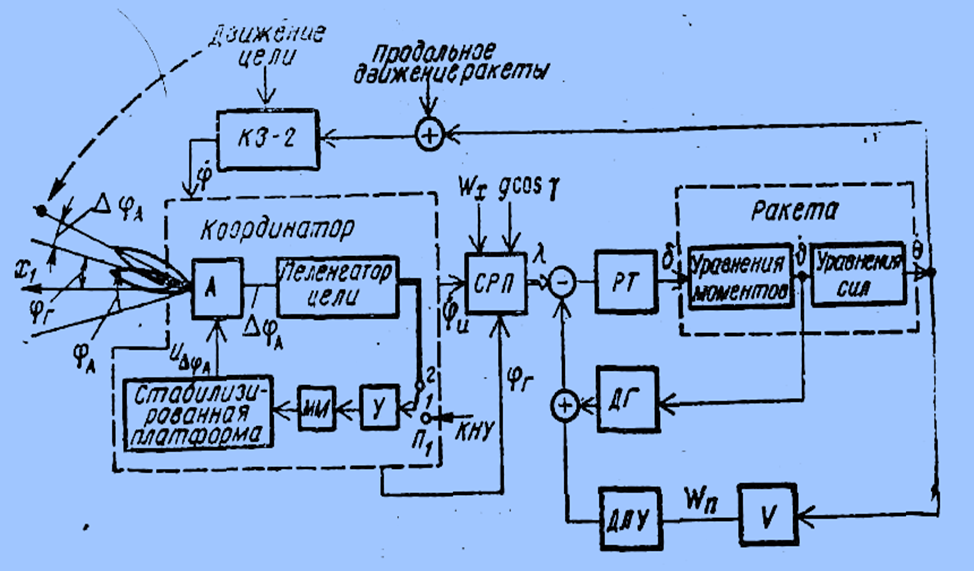
Рисунок 5 - Функциональная схема головки самонаведения ЗУР со следящим гироприводом

Перед началом самонаведения переключатель П1 находится в положении 1. Команды начальной установки (КНУ) или поиска цели, усиленные усилителем У, поступают на моментные моторы ММ и заставляют платформу прецессировать до тех пор, пока ось равносигнальной зоны не совпадет с направлением на цель.

После этого переключатель П1 устанавливается в положение 2 и начинается процесс автоматического слежения за целью.
Система, состоящая из стабилизированной платформы, моментных моторов ММ и усилителя У, называется гироприводом.

Входной величиной пеленгатора является угол отклонения цели от равносигнального направления 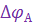, являющийся сигналом ошибки следящей системы ГСН. Этот сигнал равен нулю, если .

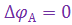При 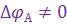напряжение ошибки, пропорциональное отклонению цели от равносигнального направления, обеспечивает разворот антенны ГСН на цель, т. е. слежение за целью. Установившееся значение ошибки слежения ГСН за целью 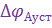будет тем больше, чем больше измеряемая угловая скорость антенны 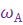и чем меньше произведение коэффициентов передачи пеленгационного устройства и гиропривода,

Выбором передаточных функций этих устройств, как в любой системе управления, обеспечивается малая величина динамических ошибок сопровождения, возможность надежного слежения за целью при допустимых углах зрения пеленгатора.

При использовании в координаторе гиростабилизированной платформы и гироскопических исполнительных устройств сравнительно просто измерить угловую скорость поворота антенны (линии ракета — цель), принимаемую при методах пропорционального или параллельного сближения за параметр рассогласования.

Кинематическое звено КЗ-2 определяет связь между движением цели, движением ракеты и угловой скоростью поворота антенны (положением линии визирования цели — углом ).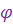

В контуре системы самонаведения счетно-решающий прибор в значительной степени выполняет те же функции, что и устройство выработки команд в командных системах управления, но в более ограниченных пределах. Так же как и в системах телеуправления, характер передаточной функции контура самонаведения в значительной мере обеспечивается выбором передаточной функции счетно-решающего прибора.

На регулярный сигнал, т. е. величину угловой скорости линии ракета — цель 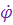, оказывают влияние: движение цели, ускорение свободного падения 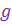и продольное ускорение ракеты 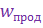. Антенна головки самонаведения устанавливается под радиопрозрачным обтекателем. Обтекатель, как правило, вносит в полученную информацию о взаимном движении цели и ракеты не только случайную, но и систематическую составляющую ошибки, вызванную преломлением электромагнитной энергии в его стенках.
При больших расстояниях 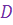как движение цели, так и движение ракеты мало влияют на угловую скорость вращения линии ракета — цель. При малых расстояниях уже небольшие изменения в положении цели и ракеты могут вызвать резкие изменения направления линии ракета — цель, привести к большим отклонениям рулей и даже срыву самонаведения.

Особенностью контура системы самонаведения по сравнению с контуром радиотелеуправления является отличие структуры кинематического звена, характеризующего относительное сближение ракеты и цели. Это обусловлено, во-первых, тем, что координатор (измерительный элемент) и счетно-решающий прибор установлены на борту ракеты, во-вторых, реализацией в системах самонаведения двухточечных методов наведения, в соответствии с которыми определяется взаимное положение двух точек — ракеты и цели.

И так, выбранный метод наведения будет определять вид передаточных функций кинематического звена, устанавливающего связь между параметром рассогласования и параметрами движения цели и ракеты, бортового координатора и счетно-решающего прибора. Передаточнаяфункция ракеты с автопилотом не отличается от соответствующей передаточной функции телеуправляемой ракеты.

Автопилот предназначен для стабилизации угловых движений зенитной управляемой ракеты относительно центра масс. Кроме того, автопилот является составной частью системы управления полетом ЗУР и управляет положением самого центра масс в пространстве в соответствии с командами управления.

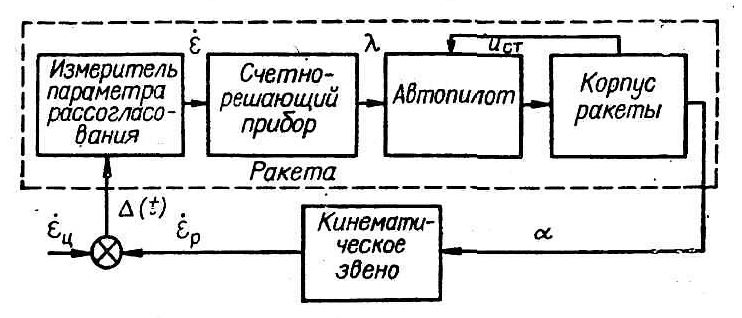
Рисунок 6 - Функциональная схема системы самонаведения