Вывод уравнения кинематического звена контура самонаведения

На рис. 7 приведены геометрические соотношения при наведении ракеты. При самонаведении ракеты в вертикальной плоскости относительное положение ракеты и цели характеризуется вектором дальности ракета — цель D, ориентацию в пространстве которого определяет угол 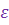, величина и скорость изменения которого зависят как от параметров движения цели, так и от параметров движения ракеты.

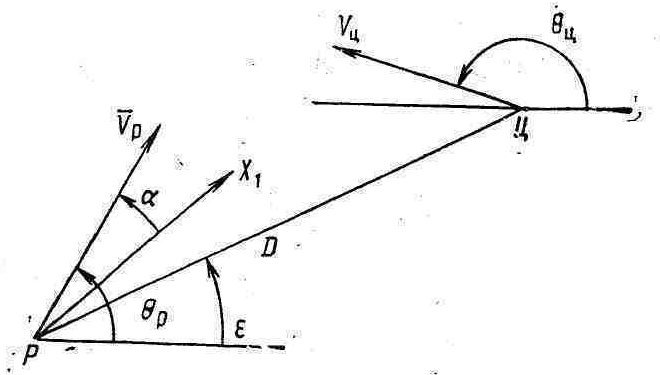
Рисунок 7 - К выводу уравнения кинематического звена контура самонаведения

Уравнения кинематики самонаведения, характеризующие скорость изменения вектора дальности и его угловую скорость вращения, имеют вид:

,

,

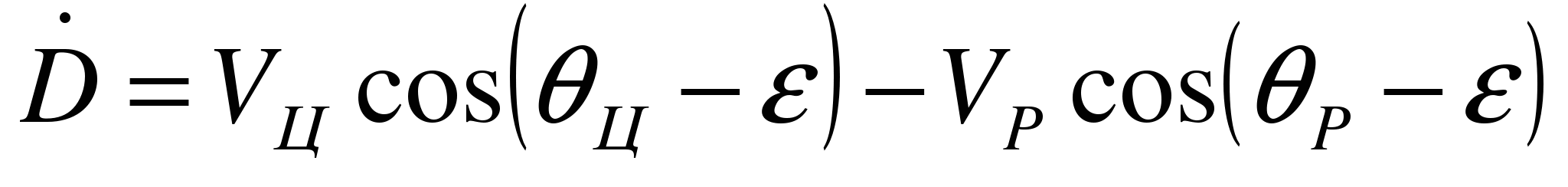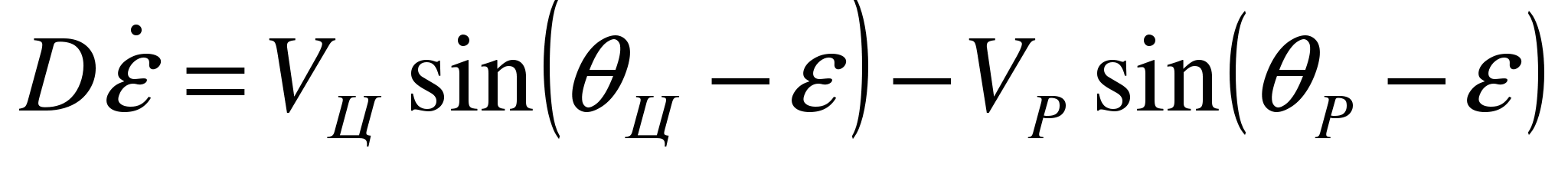где 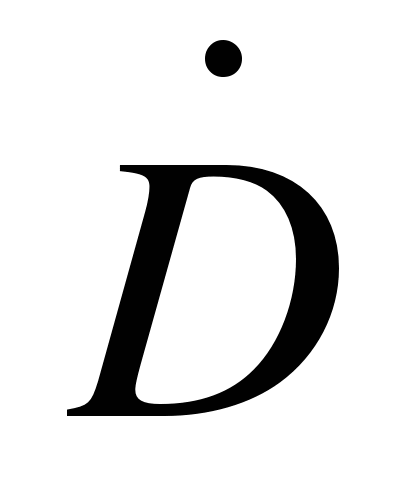, 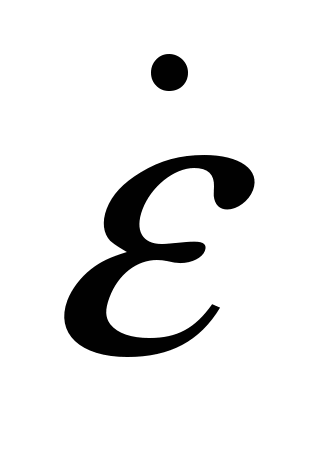— скорость изменения вектора дальности и угловая скорость его вращения соответственно;

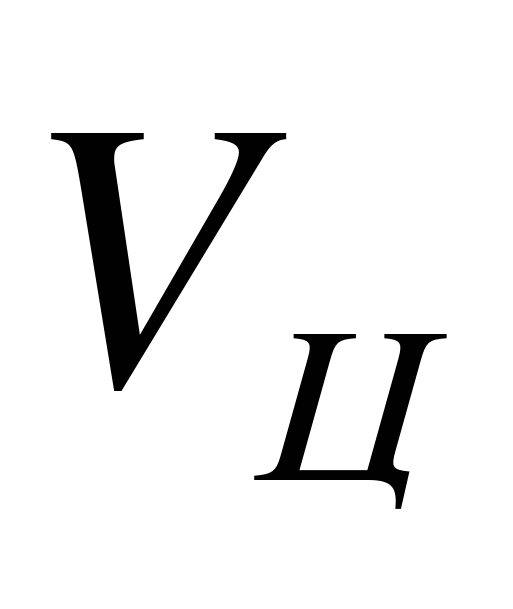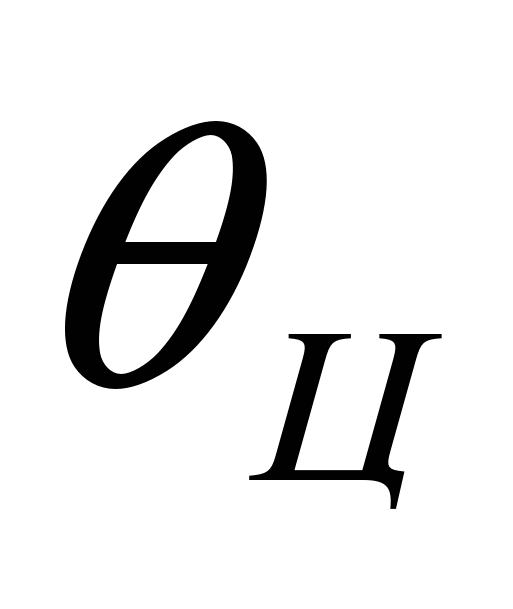, — модуль и угол наклона вектора скорости цели соответственно;

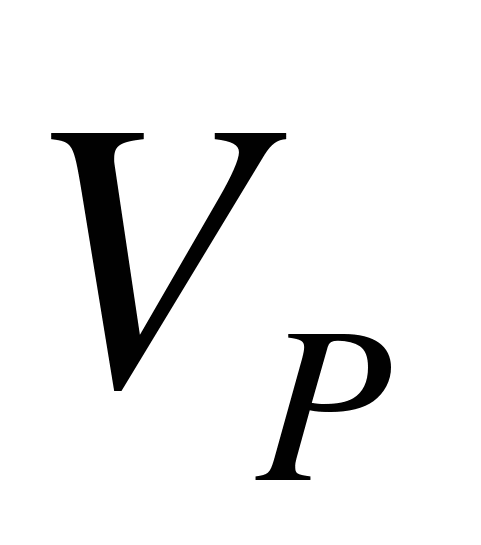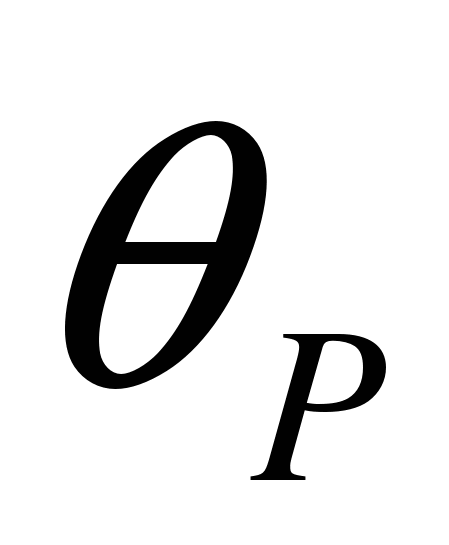, — модуль и угол наклона вектора скорости ракеты соответственно.

Рассматривая условия наведения на встречных курсах, можно допустить, что

,
,
,

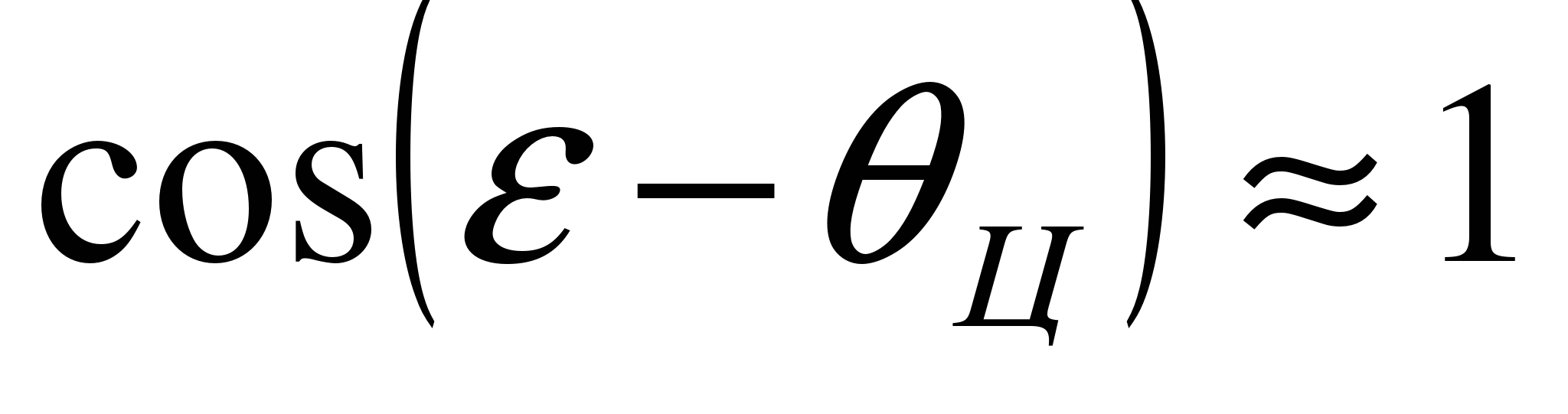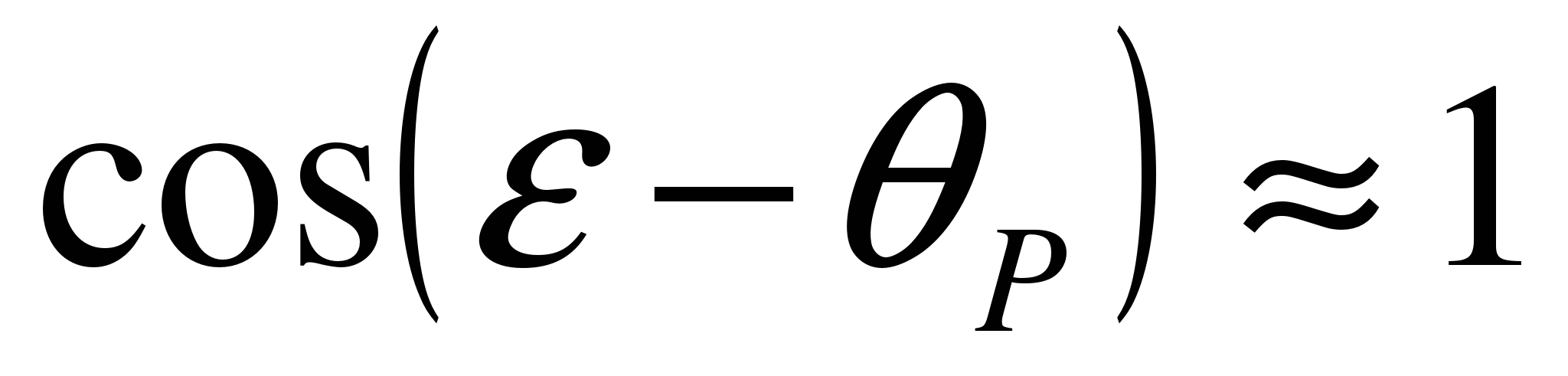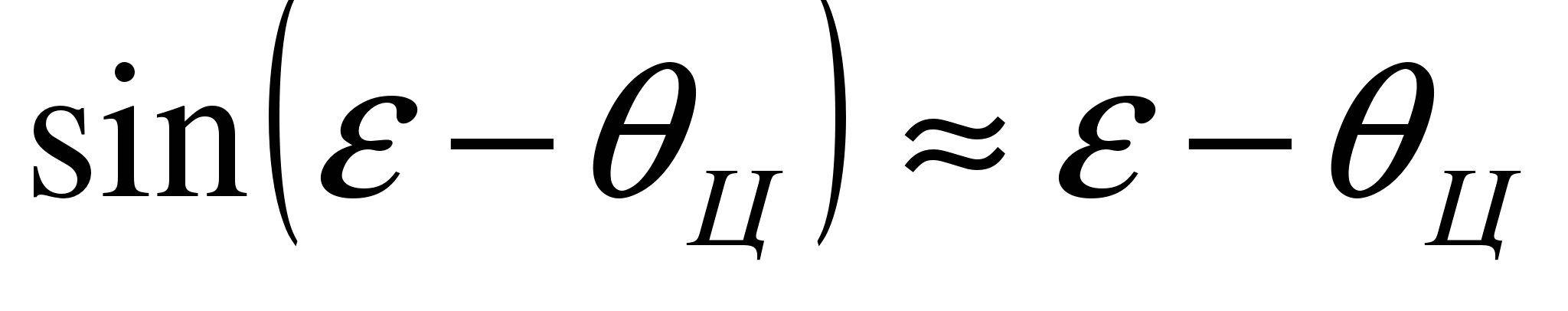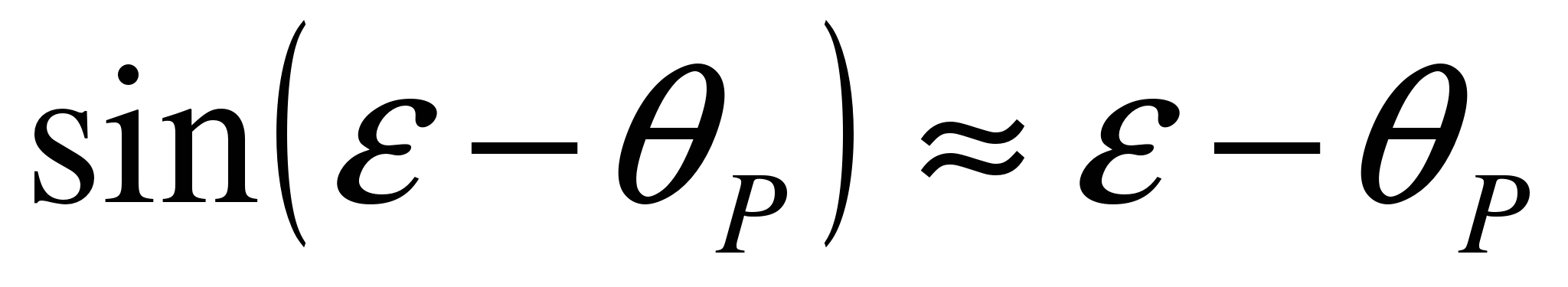
тогда получим:

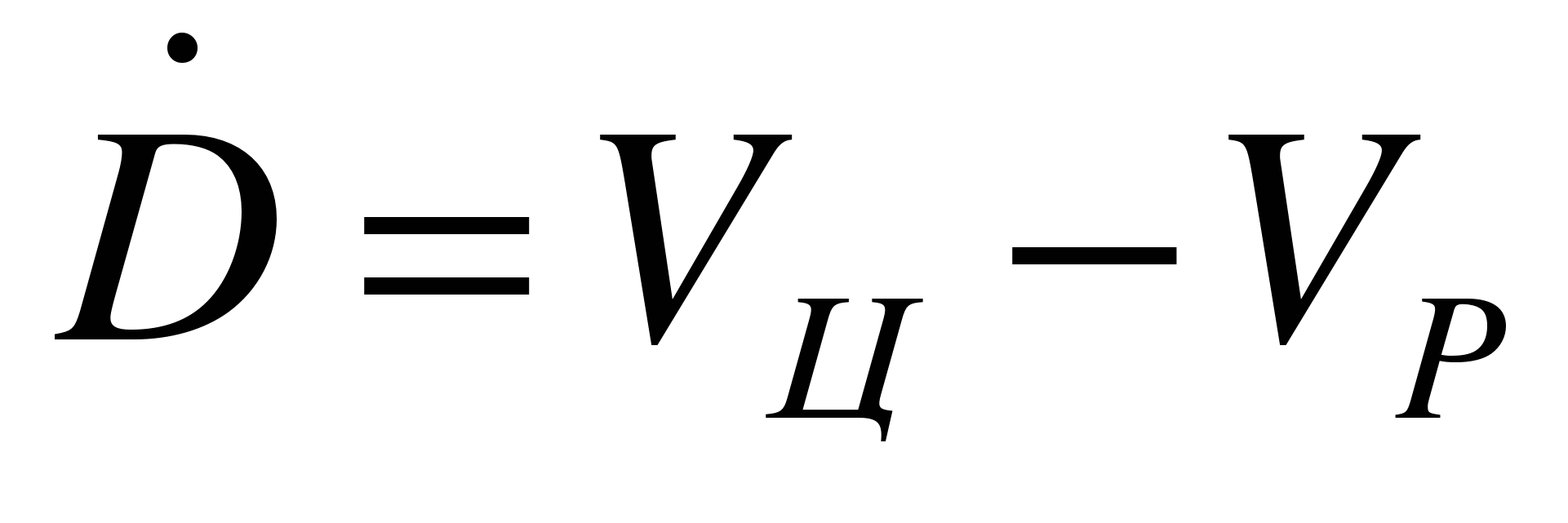
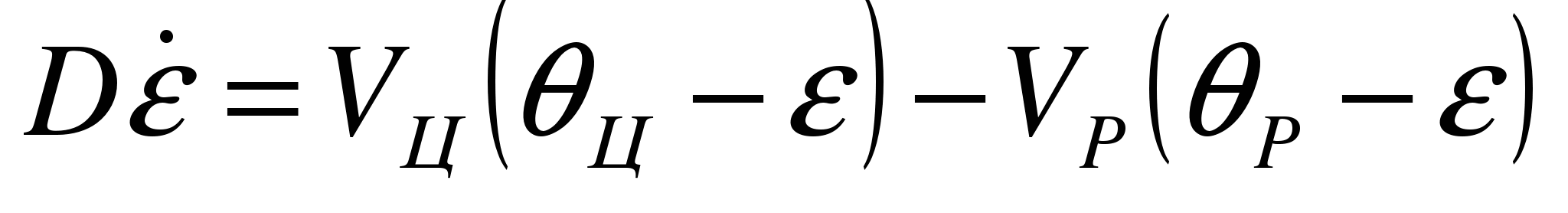
Полученные уравнения показывают, что скорость вращения линии ракета — цель обусловливается движением цели и движением ракеты перпендикулярно этой линии, т. е.

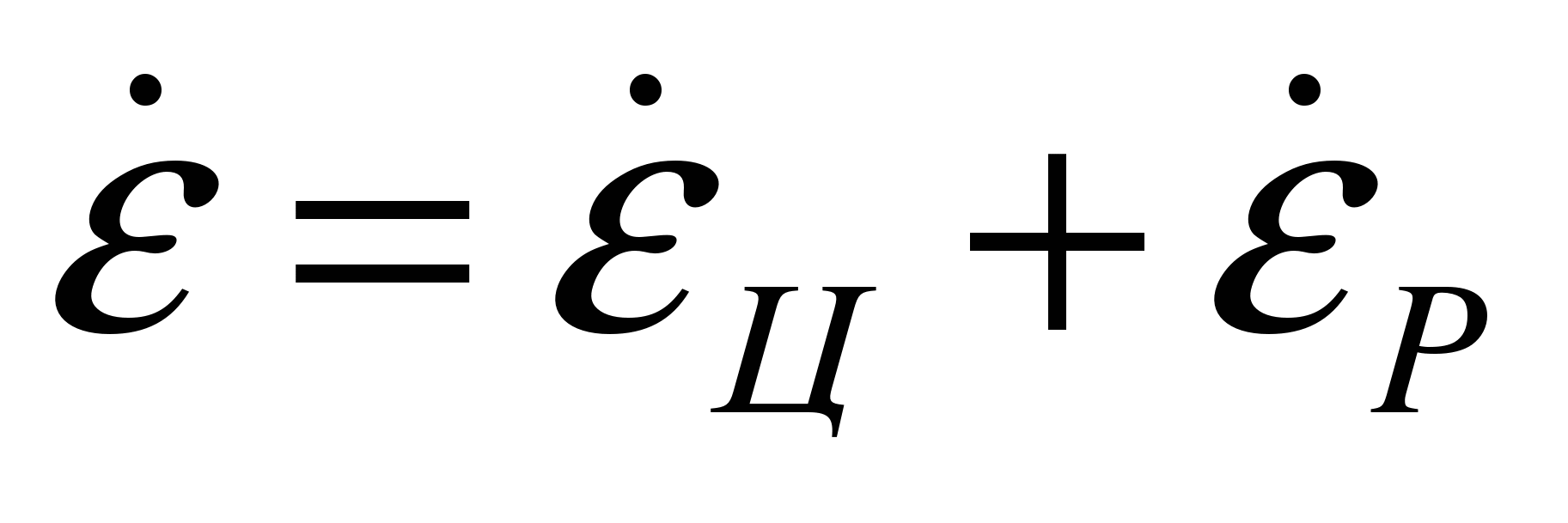
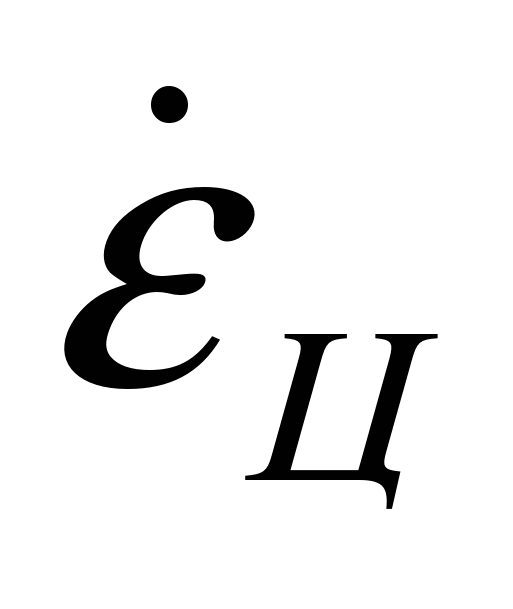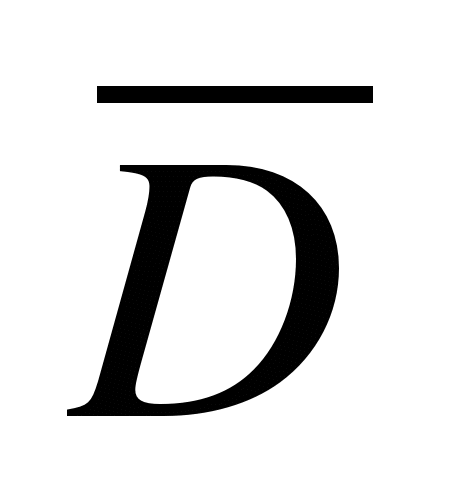где , — составляющие скорости вращения линии визирования ракета — цель (вектора ), обусловленные соответственно движением цели и ракеты.

Учитывая, что

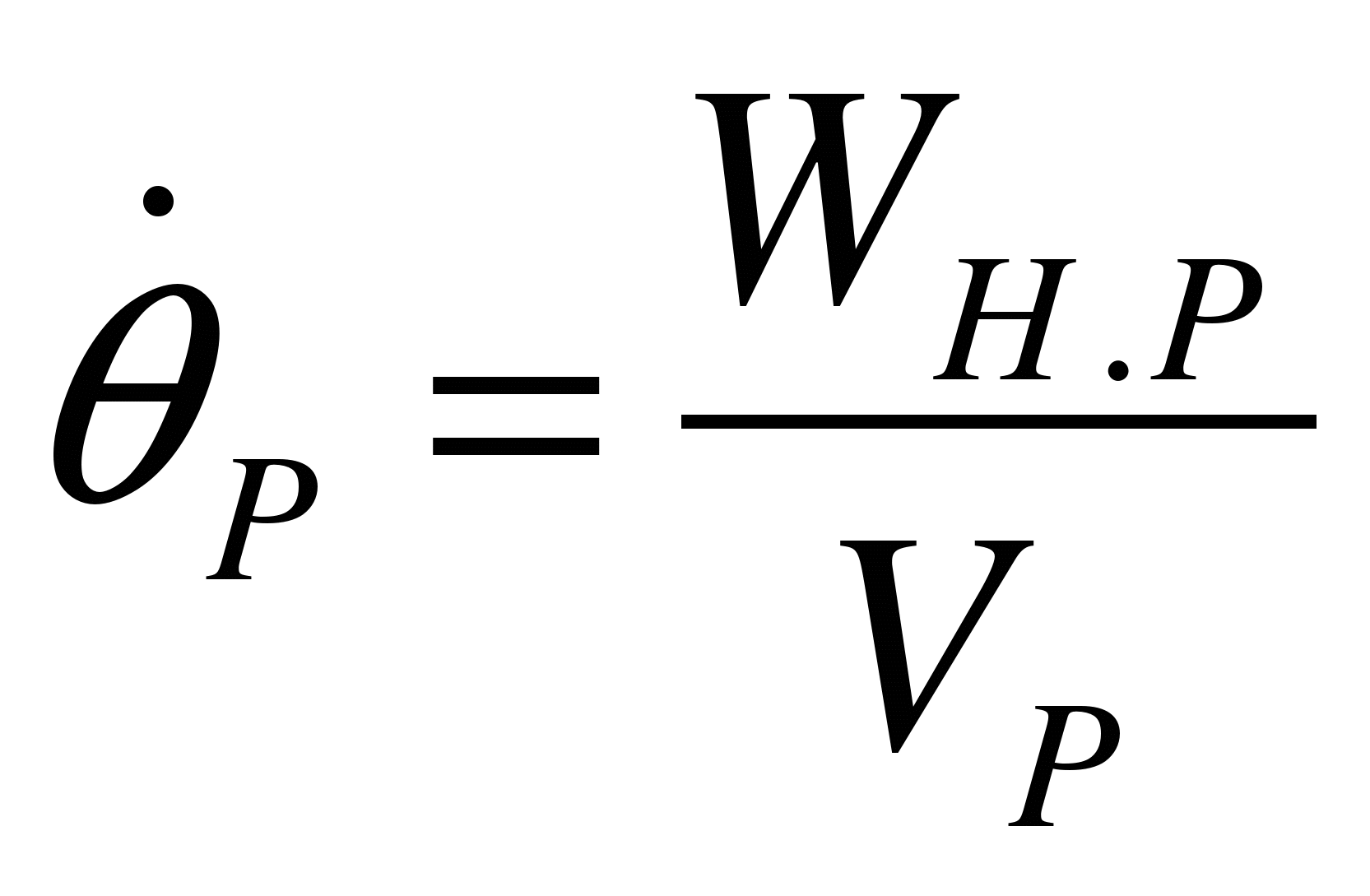, а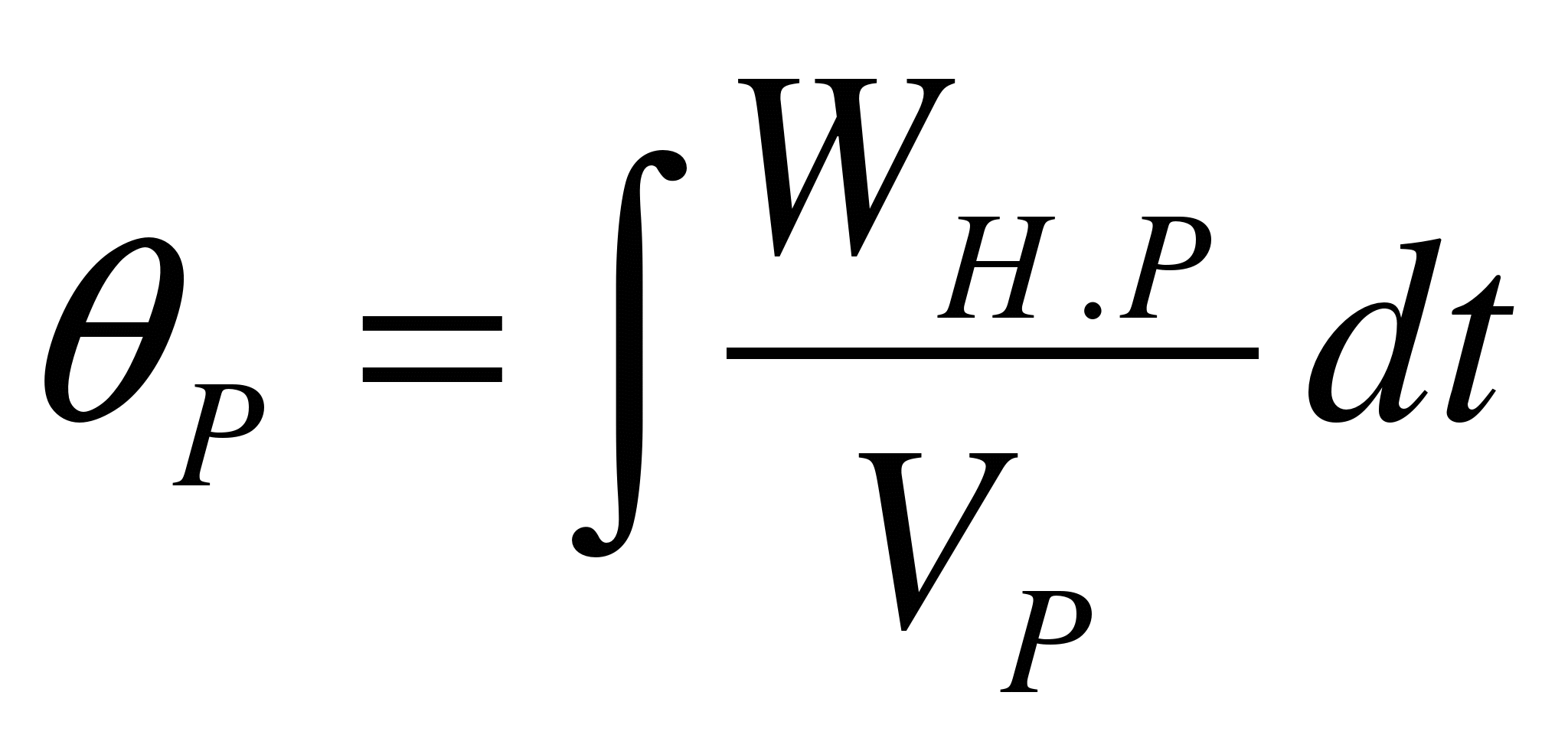

в операторной форме можно записать

,

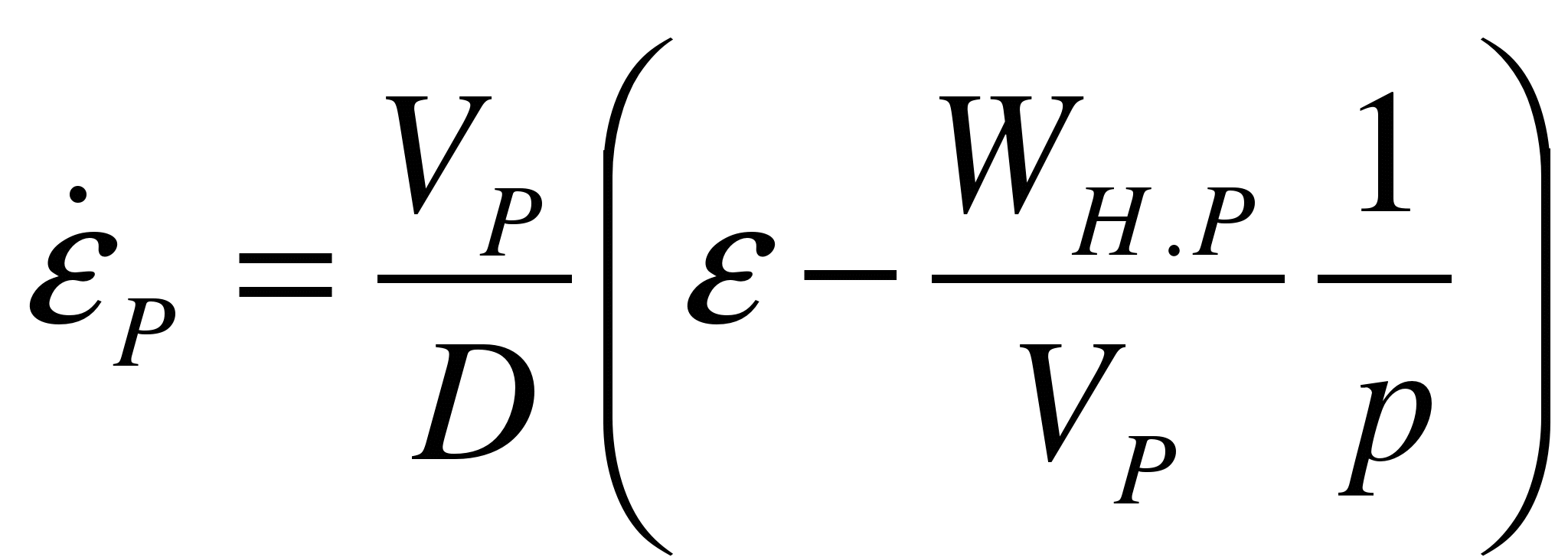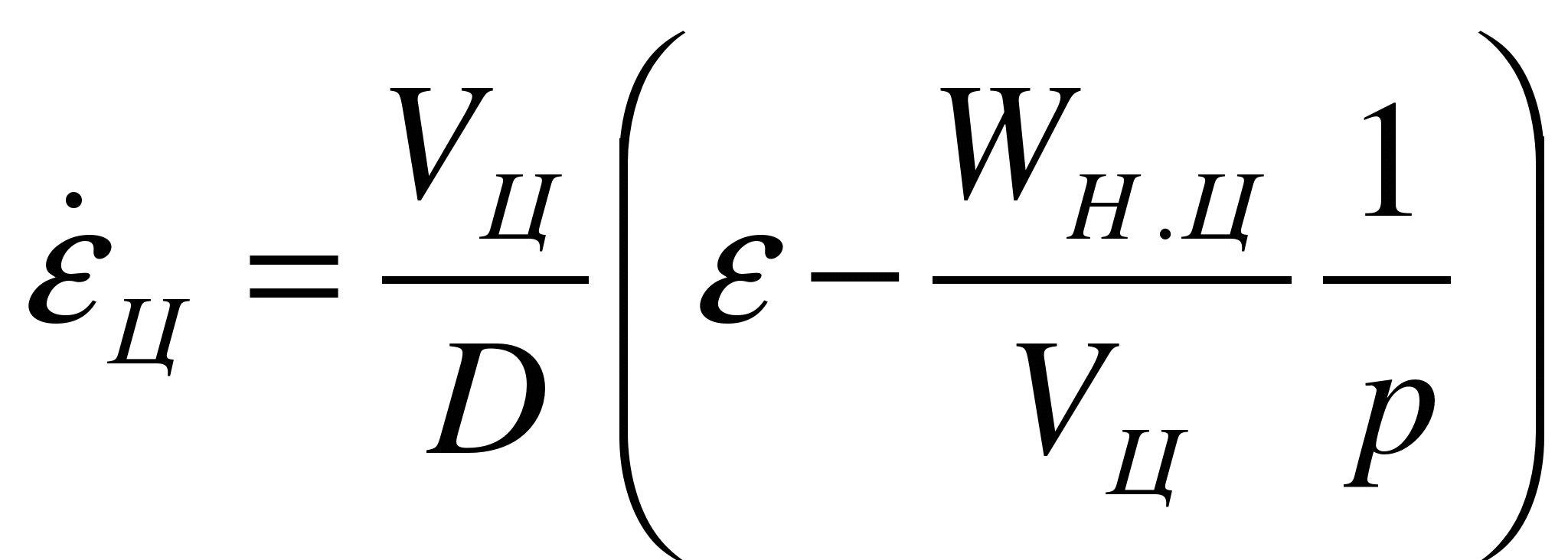
Структурная схема кинематического звена при реализации методов пропорционального и параллельного сближения показана на рис. 8.

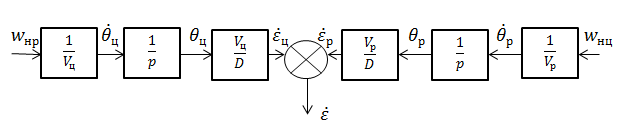Рисунок 8 - Кинематическое звено контура самонаведения

На рисунке 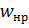, 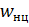- нормальные ускорения ракеты и цели.

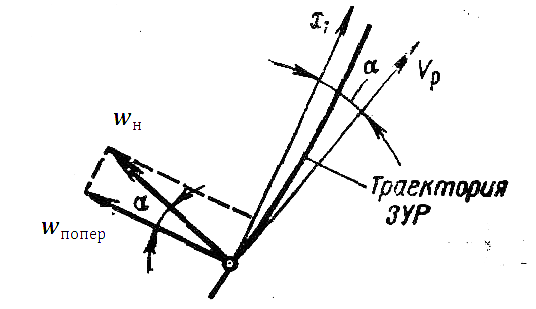
Рисунок 9 – Нормальное 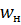и поперечное 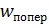ускорение ракеты, измеряемое ДЛУ

Датчики линейных ускорений (ДЛУ) ориентируются так, чтобы их оси чувствительности совпадали с поперечными осями связанной системы координат ракеты. Ускорения, измеряемые ДЛУ, в принципе не равны нормальным ускорениям ракеты. Рассогласование осей связанной и скоростной систем координат, т. е. действующих и измеряемых ускорений, учитывается поправочным коэффициентом η.

Параметры передаточной функции ракеты полностью определяют ее динамические свойства.
Коэффициент усиления ракеты 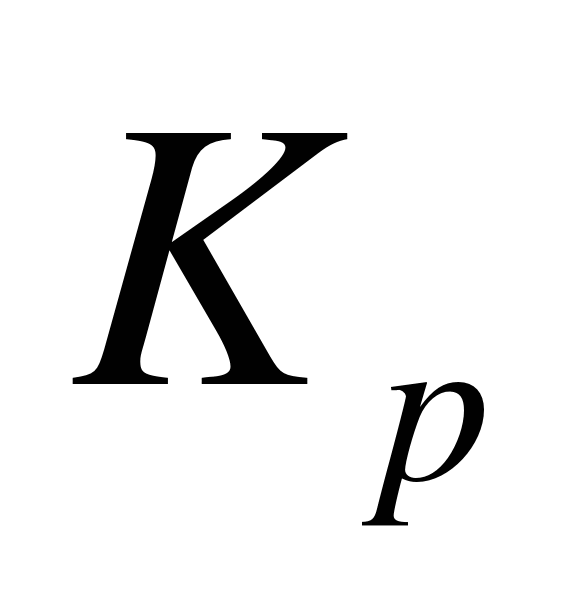характеризует маневренные свойства ракеты и определяет в установившемся режиме скорость приращения угла наклона траектории при отклонении руля на единицу угла:

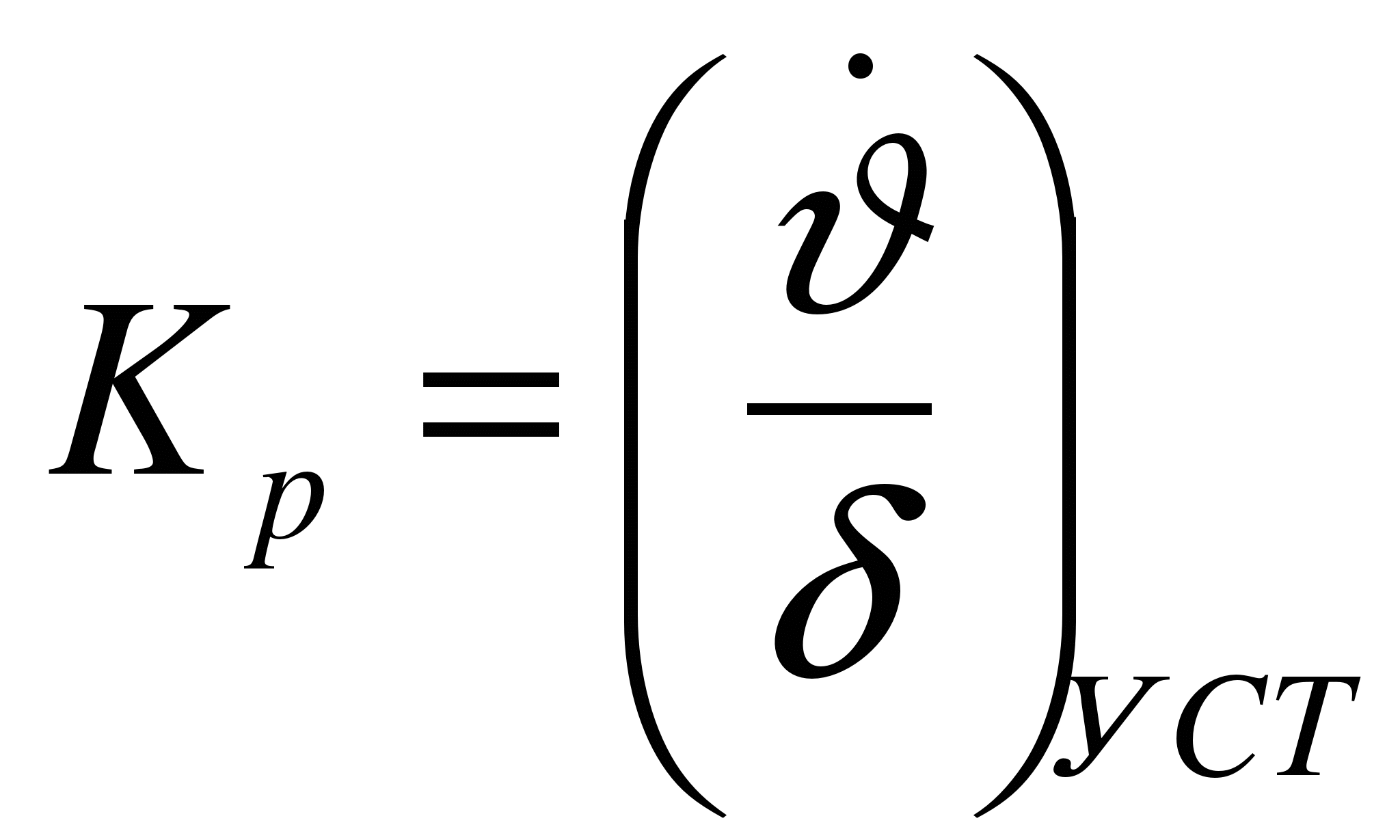
Величина этого коэффициента определяется только ракетой и вследствие ограниченности управляющих моментов и нормальных управляющих сил не может быть улучшена системой управления.
Располагаемая перегрузка ракеты связана с коэффициентом 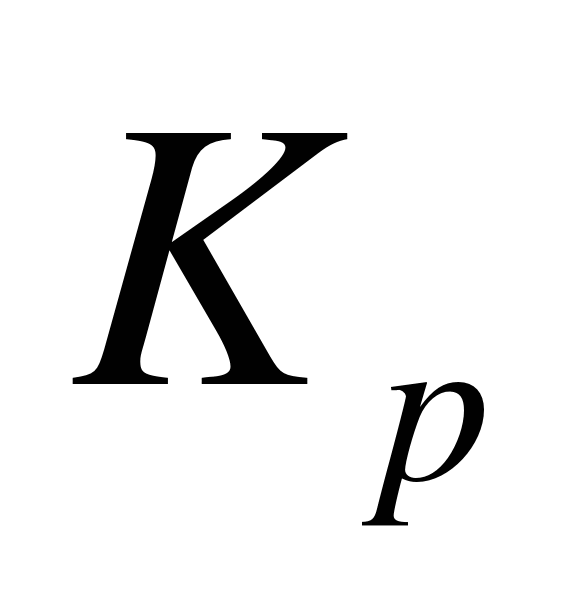зависимостью

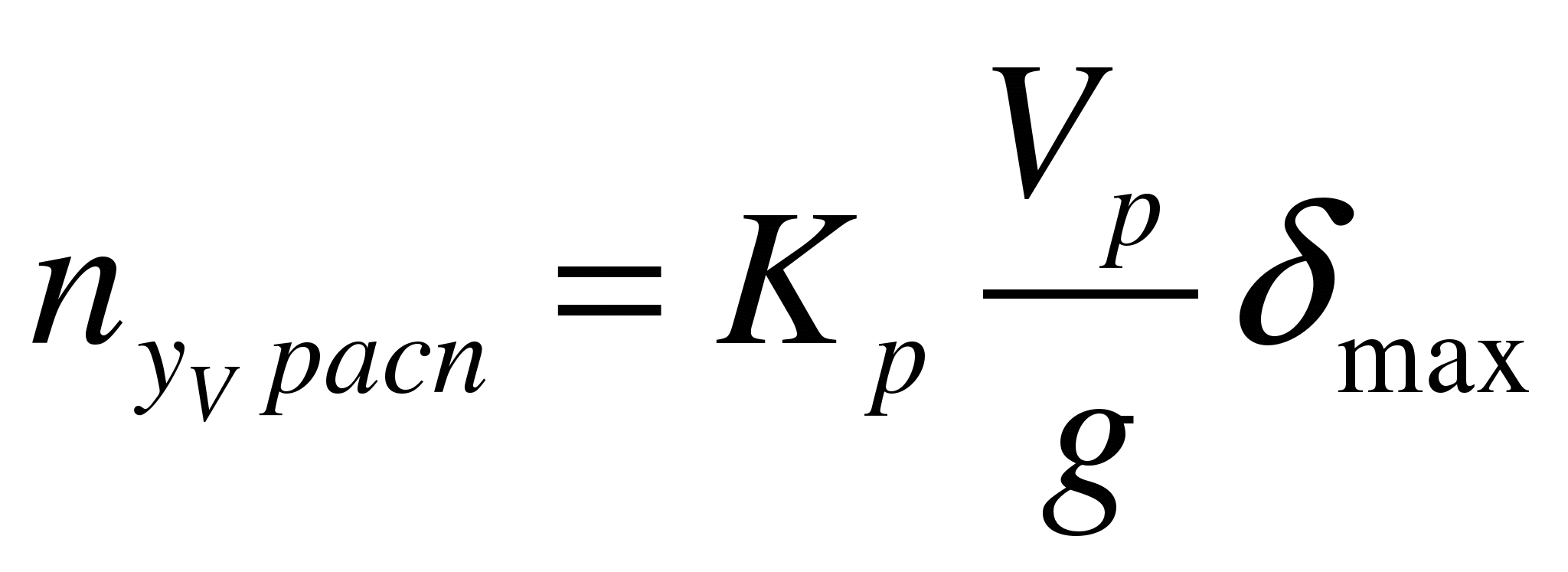
где 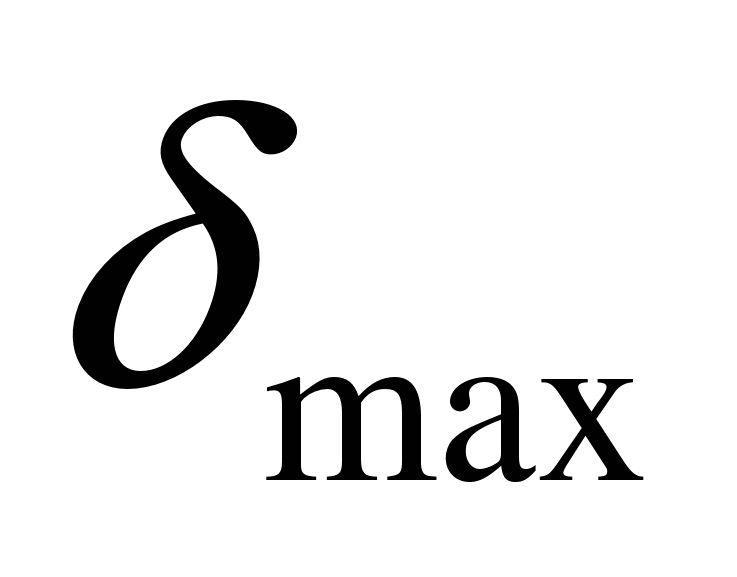— максимальное отклонение рулей высоты.
Произведение 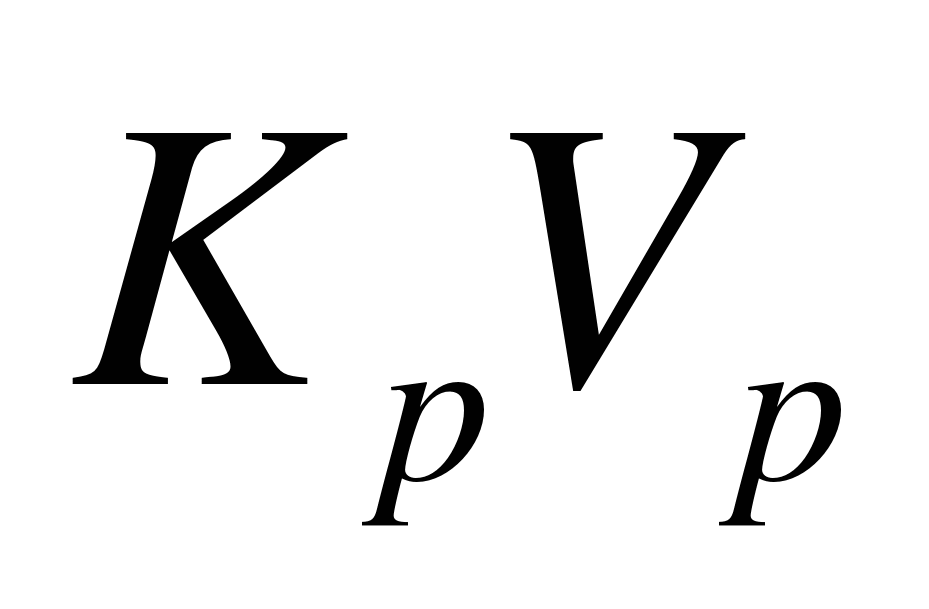принято называть передаточным числом ракеты по нормальному ускорению ( ).
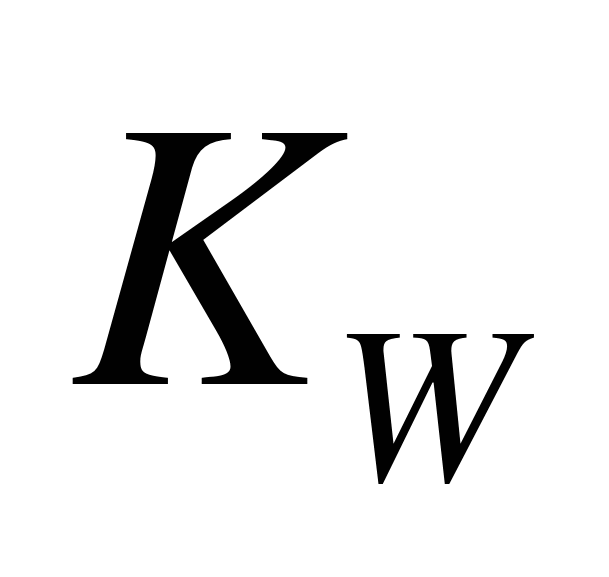Коэффициент усиления ракеты 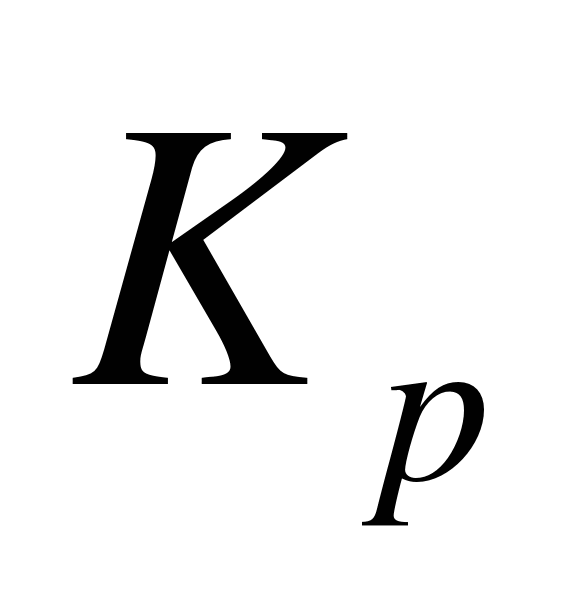, а следовательно, и коэффициент усиления контура управления 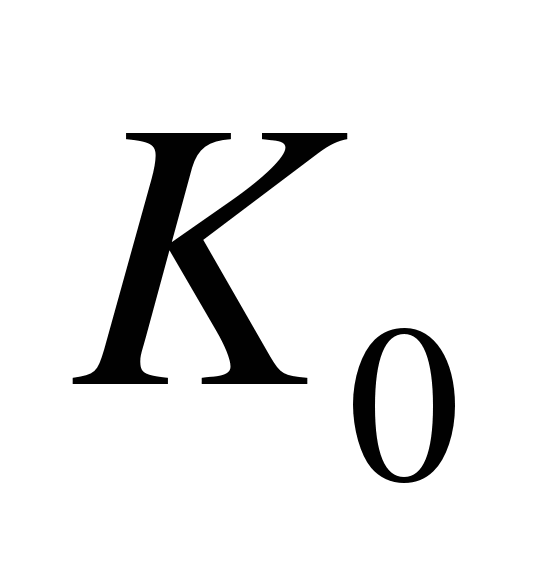зависят от скорости ракеты и плотности воздуха. С увеличением высоты полета ракеты значение коэффициента 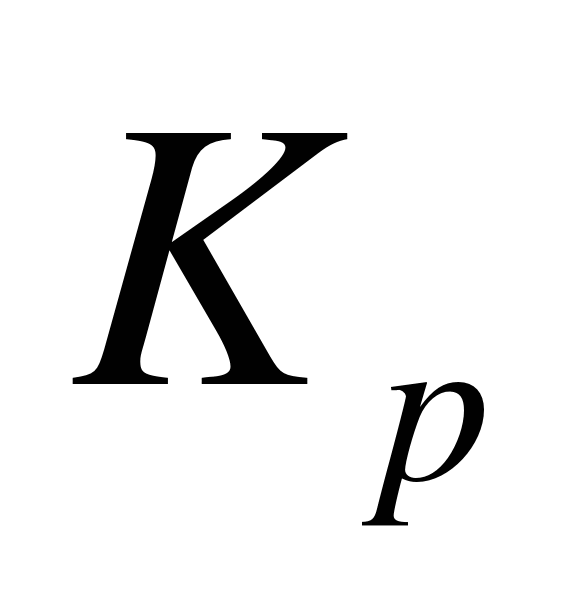падает.

Величина передаточного коэффициента 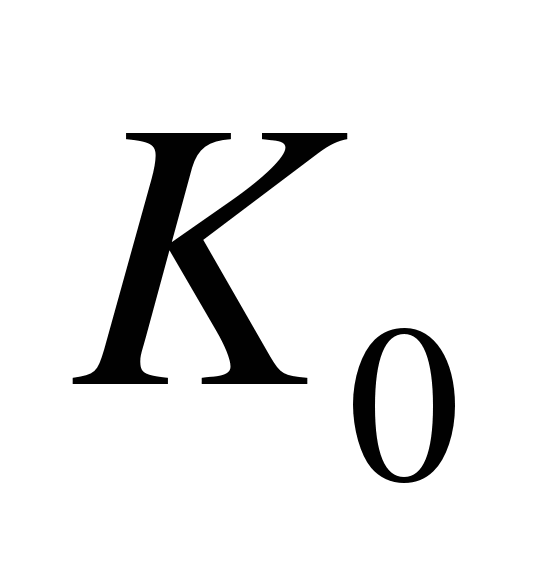, в состав которого в качестве одного из сомножителей входит коэффициент 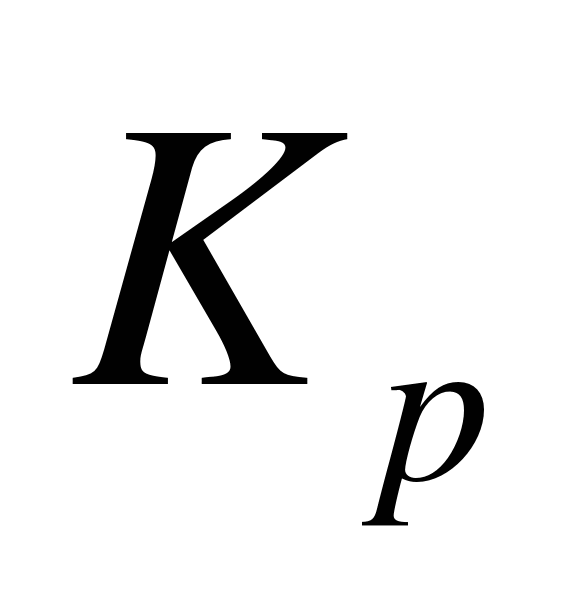, значительно влияет на точность наведения ракеты на цель. Для уменьшения влияния положения точки встречи ракеты с целью (в пределах заданной зоны обстрела) на эффективность стрельбы значение коэффициента усиления ракеты 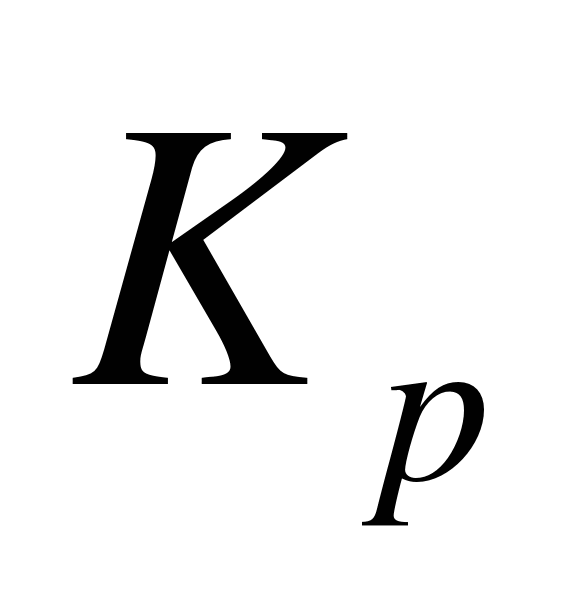необходимо стабилизировать. Наиболее действенный способ стабилизации — включение в состав ракеты устройств, корректирующих значение 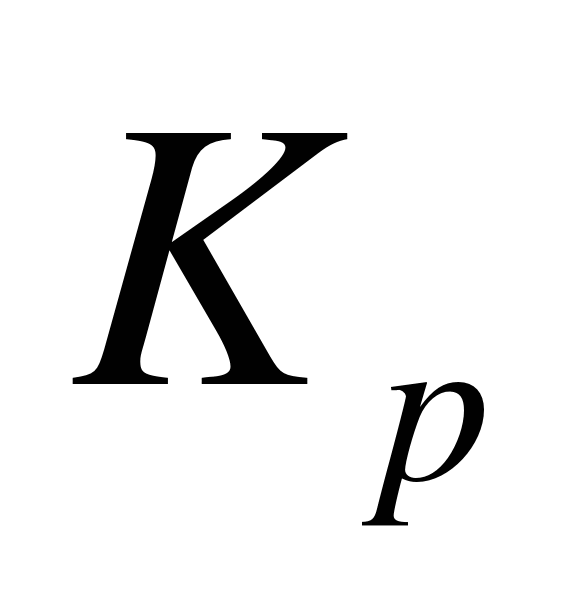в зависимости от скорости ракеты и плотности воздуха. Работа этих устройств, как правило, связана с использованием датчиков скоростного напора. Получение требуемого значения относительного коэффициента демпфирования и его стабилизация достигаются охватом, ракеты обратными связями по угловой скорости вращения ракеты и поперечному ускорению. Сигналы обратных связей формируются, как правило, совокупностью измерителей, включаемых в автопилот. Такими измерителями являются демпфирующие гироскопы (ДГ) и датчики линейных ускорений (ДЛУ).
Собственная частота колебаний также зависит от условий полета ракеты (скоростного напора, статической устойчивости) и в реальных условиях стрельбы может изменяться а широких пределах. Она должна находиться в определенном соотношении с частотой среза контура управления, выбор которой обусловливается оптимумом систематических в случайных составляющих ошибок наведения.

Датчик угловой скорости (гироскоп) ДУСиспользуется в различных системах летательных аппаратов, в частности, автопилоте и предназначен для измерения угловой скорости ракеты и самолета и выдачи электрического сигнала, пропорционального измеряемой угловой скорости.

Широкое применение нашли ДУС с поплавковыми гироскопами. В таком гироскопе жидкость выполняет роль демпфирующей среды, в которой за счет трения жидкости о стенки корпуса и кожуха при повороте последнего в результате прецессии гироскопа создается демпфирующий момент.
На корпусе ДУС обычно указывают ось, вокруг которой он измеряет скорость. Эта ось называется измерительной, на корпусе она обозначается точкой и стрелкой. ДУС обычно устанавливают вблизи центра тяжести самолёта.

С развитием многоканальных систем управления получили блочные конструкции, объединяющие в одном корпусе несколько однотипных ДУС. Такие изделия называются блоком демпфирующих гироскопов, или сокращённо – БДГ (см. рис.10 ).

Для построения контура системы самонаведения при реализации метода параллельного (пропорционального) сближения необходимо рассмотреть также функциональные зависимости для бортового координатора и счетно-решающего прибора (СРП).

При самонаведении по методу параллельного или пропорционального сближения для измерения угловой скорости вращения линии ракета — цель могут применяться бортовые координаторы со следящим гироприводом, со следящей антенной и гироскопическими датчиками угловых скоростей.

Рисунок 10 - Платформа с ДУС в отсеке самолёта

Входным воздействием координатора является значение угла 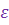. На выходе координатора формируется сигнал

,

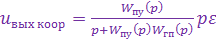где 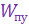, 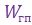—передаточные функции пеленгатора и гиропривода соответственно.

Координатор со следящим гироприводом обеспечивает измерение угловой скорости линии ракета — цель в стабилизированной системе координат, в то же время позволяет осуществить достаточно точное слежение за целью по угловым координатам.
Связь между сигналом рассогласования и формируемой СРП командой управления может быть представлена в виде

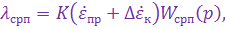
где К — коэффициент преобразования;

— измеренное значение угловой скорости антенны;

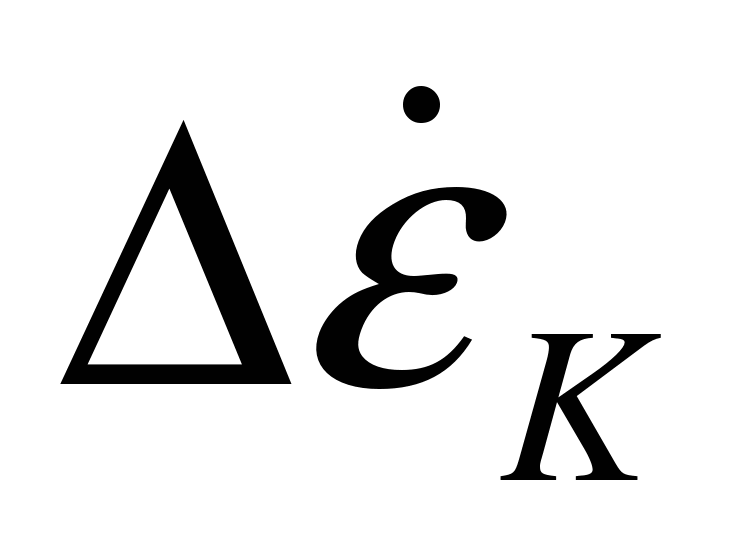— компенсационная составляющая угловой скорости, обусловленная действием силы тяжести, продольным ускорением ЗУР и преломлением обтекателя;

— передаточная функция счетно-решающего прибора.

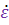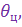
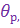
На рис. 11 показан контур системы самонаведения при реализации метода пропорционального или параллельного сближения. Видим, что параметр рассогласования является входным воздействием контура управления; при постоянных значениях 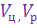величина его будет изменяться тем быстрее, чем ближе ракетa к цели. Поскольку звено 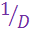вконтур включено последовательно, то коэффициент усиления контура с уменьшением D будет возрастать, увеличивая чувствительность системы управления, что приводит к увеличению точности наведения по мере сближения ракеты с целью.

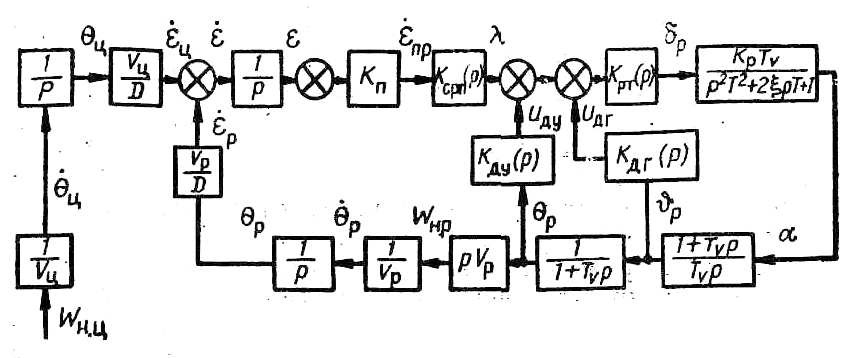
Рисунок 11 - Контур системы самонаведения при реализации метода параллельного (пропорционального) сближения: ДГ – демпфирующий гироскоп, ДУ – датчик линейных ускорений

Это положение является принципиальным отличием данной системы от системы командного управления, в которой, как ранее отмечалось, по мере удаления ракеты от пункта управления точность наведения уменьшается.
Однако начиная с некоторой дальности D коэффициент усиления контура становится настолько большим, что контур возбуждается (нарушается условие запаса устойчивости контура управления по амплитуде) и управление становится невозможным, т. е. полет ракеты становится неуправляемым.
Для уменьшения размеров «мертвой» зоны необходимо уменьшать инерционность звена автопилот — ракета, что в свою очередь требует увеличения маневренных свойств ракеты.

Другой причиной нарушения процесса управления может послужить выход за пределы угла зрения пеленгатора линейных размеров цели при малой дальности между ракетой и целью. Например, при максимальном линейном размере цели 15—30 м и по­лезном угле зрения пеленгатора в 10° «мертвая» зона может быть на дальности 75—150 м.

ПРИЛОЖЕНИЕ 1

Передаточные функции типовых звеньев

№	Тип звена	Передаточная функция звена
	Позиционные звенья	Безинерционное (элементарный усилитель)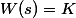
	Апереиодическое звено 1-го порядка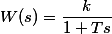
	Апереиодическое звено 2-го порядка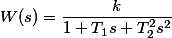
	Колебательное звено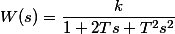
	Консервативное звено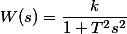
	Интегрирующие звенья	Идеальное интегрирующее звено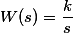
	Интегрирующее звено c замедлением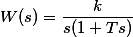
	Изодромное звено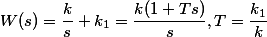
	Дифференцирующие звенья	Идеальное дифференцирующее звено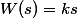
	Дифференцирующее звено с замедлением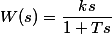

ПРИЛОЖЕНИЕ 2