Перевод смешанных чисел

Для перевода смешанного числа из одной системы счисления в другую переводят отдельно целую и дробную часть по соответствующим правилам и записывают в новой системе, разделяя десятичной запятой.

Пример

Перевести 38,8125₁₀ в 2-ную систему 38₁₀=00100110₂, а 0,8125₁₀ = 0.1101₂ следовательно 38,8125₁₀=00100110,1101₂

Тема 1.3 Логические функции

Для создания логических принципов и логических структур вычислительной техники, были введены так называемые Логические функции Булевой алгебры, которые имеют под собой реальные физические схемы, их реализующие.

Логическая функция - это функция логических переменных, которая может принимать только два значения : 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения : 0 или 1.

Логический элемент - это устройство, реализующее ту или иную логическую функцию.

Y=f(X1,X2,X3,...,Xn) - логическая функция, она может быть задана таблицей, которая называется таблицей истинности.

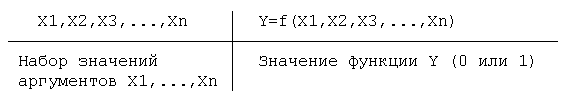
Число строк в таблице - это число возможных наборов значений аргументов. Оно равно 2ⁿ, где n - число переменных. Число различных функций n переменных равно 2^{2^n}.

Отрицание

Инвертирует значение операнда.

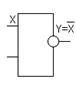
Функция Y=f(X)=NOT(X) - отрицание НЕ или инверсия (NOT(X) - это НЕ X). Техническая реализация этой функции - инвертор на любом транзисторе или логическом элементе, или транзисторный ключ. Таблица истинности функции отрицания имеет вид (рис.1.3.1 , а). Логический элемент НЕ обозначается на схемах следующим образом: (рис. 1.3.1 , б) (пишется X c чертой сверху)

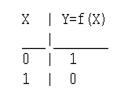
а б

Рис.1.3.1 Логический элемент ОТРИЦАНИЕ НЕ

а - таблица истинности; б – условное графическое изображение;

2. Логическое ИЛИ (логическое сложение, дизъюнкция):

Принимает значение 1, когда хоть один из операндов равен 1.

Y= X1 + X2 = X1VX2

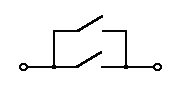
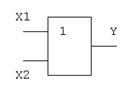
Техническая реализация этой функции - два параллельно соединенных ключа (рис.1.3.2а). Логический элемент ИЛИ обозначается на схемах следующим образом. (рис. 1.3.2 б).

Таблица истинности логического ИЛИ имеет вид (рис.1.3.2 в).

:

а б в

Рис.1.3.2Логический элемент ИЛИ:

а - техническая реализация; б – условное графическое изображение; в - таблица истинности.

3. Логическое И (логическое умножение, конъюнкция, схема совпадений):

Принимает значение 1, только, когда оба операнда равны 1.

Y = X1X2 = X1&X2

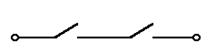
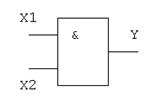
Техническая реализация этой функции - два последовательно соединенных ключа (рис. 1.4.3 а).

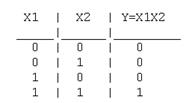
Таблица истинности логического И имеет вид (рис.1.3.3 в) Логический элемент И обозначается на схемах следующим образом. (рис. 1.3.3 б).:

: а б в

Рис.1.3.3Логический элемент ИЛИ:

а - техническая реализация; б – условное графическое изображение; в - таблица истинности.

4. Функция стрелка Пирса (ИЛИ-НЕ):

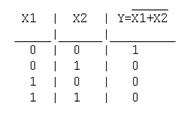
Y = NOT(X1+X2)

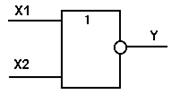
Таблица истинности функции ИЛИ-НЕ имеет вид (рис. 1.3.4 а). Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом (рис. 1.3.4 б).:

а б

Рис.1.3.4 Логический элемент ИЛИ:

а - таблица истинности; б – условное графическое изображение.

5. Функция штрих Шеффера (И-НЕ):

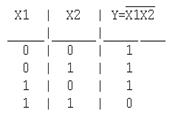
Y = X1|X2 = NOT (X1X2)

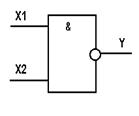
Таблица истинности функции И-НЕ имеет вид (рис. 1.3.5 а): Логический элемент И-НЕ обозначается на схемах следующим образом (рис. 1.3.5 б)

: а б

Рис. 1.3.5 Логический элемент ИЛИ:

а - таблица истинности; б – условное графическое изображение