Вероятностный смысл энтропии
Для любой термодинамической системы различают макросостояние и микросостояние. Макросостояние системы характеризуется макропараметрами (Т, Р, V, U и т.д.). В то же время система состоит из бесконечно большого количества микрочастиц. Микросостояние – это расположение и энергия отдельных молекул в данный момент времени.
Одно макроскопическое состояние системы может реализоваться несколькими разными микросостояниями. Для каждого микросостояния существует вероятность (Р) того, что система находится именно в этом микросостоянии. Поэтому все процессы в термодинамике носят вероятностный или статистический характер, определяющий переход системы из менее вероятного в более вероятное состояние.
Больцман в 1896 г. постулировал, что энтропия связана с термодинамической вероятностью логарифмической зависимостью
S = k ln W  уравнение Больцмана
уравнение Больцмана
k – константа Больцмана: k = 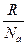 = 1,38∙10-23 Дж/градус;
= 1,38∙10-23 Дж/градус;
W – число микросостояний, с помощью которых можно реализовать данное макросостояние: W=1/Р;
Р – вероятность того, что система находится именно в этом микросостоянии.
С увеличением порядка в системе уменьшается число микросостояний, с помощью которых можно реализовать это состояние, и уменьшается энтропия.
При переходе вещества из газообразного состояния в жидкое и далее в кристаллическое энтропия уменьшается. Согласно уравнению Больцмана энтропия может быть равна нулю только в одном единственном состоянии.
В 1911 г. Планк сформулировал постулат, известный как третий закон термодинамики:
энтропия идеально построенного кристалла чистого вещества
(без дефектов и примесей) при абсолютном нуле равна нулю.
Этот закон устанавливает нуль отсчета для энтропии, что позволяет рассчитывать её абсолютное значение, т.к.
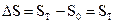
В изолированной системе (U, V=const) в самопроизвольном процессе возрастает энтропия. В состоянии равновесия энтропия максимальна и постоянна.
В закрытой и открытой системе критерием самопроизвольного протекания процесса является уменьшение энергии Гиббса (G).
G=H-TS
H – энтальпия
T – температура
S – энтропия
Используя энергию Гиббса, второй закон термодинамики можно выразить так:
При постоянстве температуры и давления в системе самопроизвольно протекают только процессы, ведущие к уменьшению энергии Гиббса. В состоянии равновесия энергия Гиббса равна нулю.
∆G ≤0 (р, Т=const)
При ∆G<0 реакция самопроизвольно протекает в прямом направлении;
∆G>0 в обратном направлении
∆G=0 реакция находится в состоянии равновесия.
Изменение энергии Гиббса определяется формулой
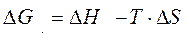
Первое слагаемое называют энтальпийным фактором, второе – энтропийным фактором. Уменьшению энергии Гиббса, а значит и самопроизвольному протеканию процесса, способствует уменьшение ∆Н (процессы с выделением тепла) и рост энтропии (процессы с ростом разупорядоченности в системе).
Стандартная энергия Гиббса химической реакции рассчитывается по формуле с использованием табличных данных:
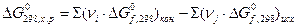
или
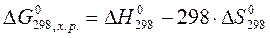 ,
,
где
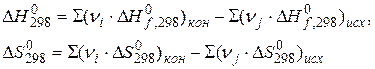
Экзергонические процессы – химические реакции, в результате которых уменьшается энергия Гиббса и система совершает работу.
Эндергонические процессы – химические реакции, в результате которых возрастает энергия Гиббса и над системой совершается работа.
Например, окисление глюкозы в крови процесс экзергонический, поскольку, сопровождается уменьшениемэнергии Гиббса, а в результате этой реакции возможно осуществлять различные виды работ в организме.
Приложение 2: Вопросы для самоконтроля
1. Что изучает химическая термодинамика?
2. Что называют параметрами состояния?
3. Чем отличаются интенсивные и экстенсивные параметры?
4. Какую функцию можно назвать функцией состояния?
5. Дайте определения понятий внутренняя энергия, теплота, работа.
6. Какие типы термодинамических систем вам известны? Чем они отличаются?
7. Какие типы термодинамических процессов выделяют?
8. Сформулируйте первое начало термодинамики.
9. Дайте определения понятий энтальпия, стандартная энтальпия образования вещества, стандартная энтальпия сгорания вещества.
10. Что такое стандартная энтальпия реакции? Какие способы её расчёта известны?
11. Сформулируйте закон Гесса.
12. Сформулируйте второе начало термодинамики. Что оно позволяет спрогнозировать?
13. Обратимые и необратимые в термодинамическом смысле процессы.
14. Дайте определение понятия энтропия.
15. Энергия Гиббса. Прогнозирование направления самопроизвольно протекающих процессов в изолированной и закрытой системах; роль энтальпийного и энтропийного факторов.
16. Термодинамические условия равновесия.
17. Что такое стандартная энергия Гиббса образования вещества, стандартная энергия Гиббса биологического окисления вещества, стандартная энергия Гиббса реакции?
18. Поясните понятие экзергонических и эндергонических процессов, протекающих в организме, принцип энергетического сопряжения.
Приложение 3: Тренировочный тест
1) Термодинамика изучает:
а) взаимосвязь теплоты и энергии;
б) скорость протекания химических процессов;
в) свойства основных классов химических соединений;
2) Энтропия - это…
а) теплосодержание участников реакции;
б) способность совершать работу;
в) мера неупорядоченности в системе;
3) Первый закон термодинамики описывает:
а) энтропию термодинамической системы;
б) связь между внутренней энергией, теплотой и работой;
в) динамическую вязкость веществ.
4) Самопроизвольно протекают процессы, сопровождаемые:
а) уменьшением энергии;
б) уменьшением энтропии;
в) увеличением энтропии.
5) Закрытая система характеризуется:
а) отсутствием обмена веществом и энергией;
б) отсутствием обмена энергией;
в) отсутствием обмена веществом;
Ответы: 1а, 2в, 3б, 4в, 5в
Приложение 4: Ситуационные задачи
1) Вычислите тепловой эффект реакции
4 НСl(газ) + О2(газ) = 2 Н2О(газ) + 2 Сl2(газ)
при 298 К и ΔН0обр. НСl(газ) = -92,30 кДж/моль,
ΔН0обр. Н2О(газ) = -241,84 кДж/моль.
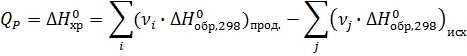
2) Вычислите тепловой эффект реакции
3 С2Н2 (газ) = С6Н6 (жид) при 298 К и
ΔН0сгор. С2Н2 (газ) = -1299,63 кДж/моль,
ΔН0сгор. С6Н6 (жид) = -3267,70 кДж/моль.
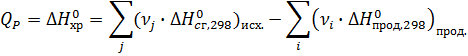
3) Вычислите изменение энтропии при 298 К (ΔS0298) для реакции
4 НСl(газ) +О2 (газ) = 2 Н2О(газ)+ 2Сl2(газ) ,
если S0298 (H2O(газ)) = 188,8 Дж/(моль·К);
S0298 (Сl2 (газ)) = 233,0 Дж/(моль·К);
S0298 (HCl(газ)) = 186,7 Дж/(моль·К);
S0298 (O2 (газ)) = 205,3 Дж/(моль·К).
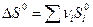 прод -
прод - 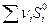 исх
исх
4) Для химической реакции вычислить изменение энергии Гиббса ΔG0298, используя стандартные значения энергии Гиббса ΔG0f, 298 и используя ΔН0298 и ΔS0298.
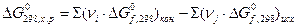
или
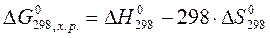
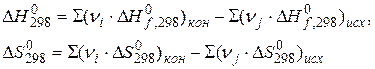
Дата добавления: 2021-09-07; просмотров: 945;











