Предел пропорциональности
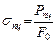 ; (2.3)
; (2.3)
2. Предел упругости
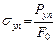 ; (2.4)
; (2.4)
3. Предел текучести
 ; (2.5)
; (2.5)
4. Предел прочности или временное сопротивление
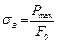 ; (2.6)
; (2.6)
5. Напряжение в момент разрыва
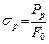 . (2.7)
. (2.7)
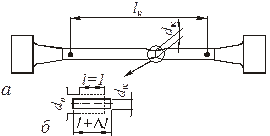
Рисунок. 2.3 – Вид цилиндрического образца после разрушения (а) и изменение зоны образца вблизи места разрыва (б)
Чтобы диаграмма отражала только свойства материала (независимо от размеров образца), ее перестраивают в относительных координатах 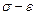 (напряжение-деформация).
(напряжение-деформация).
Ординаты произвольной i-той точки такой диаграммы (рис. 2.4) получают делением значений растягивающей силы  (рис. 2.2) на первоначальную площадь поперечного сечения образца (
(рис. 2.2) на первоначальную площадь поперечного сечения образца ( 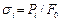 ), а абсциссы – делением абсолютного удлинения рабочей части образца
), а абсциссы – делением абсолютного удлинения рабочей части образца 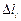 на первоначальную её длину (
на первоначальную её длину (  ). В частности для характерных точек диаграммы ординаты вычисляют по формулам (2.3)…(2.7).
). В частности для характерных точек диаграммы ординаты вычисляют по формулам (2.3)…(2.7).
Полученную диаграмму называют условной диаграммой напряжений (рис. 2.4).
Условность диаграммы заключается в способе определения напряжения не по текущей площади поперечного сечения, изменяющейся в процессе испытаний, а по первоначальной – 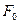 .Диаграмма напряжений сохраняет все особенности .исходной диаграммы растяжения. Характерные напряжения диаграммы называются предельными и отражают свойства прочности испытуемого материала. (формулы 2.3…2.7). Заметим, что поучаемый в этом случае предел текучести металла соответствует новому физическому состоянию металла и поэтому называется физическим пределом текучести
.Диаграмма напряжений сохраняет все особенности .исходной диаграммы растяжения. Характерные напряжения диаграммы называются предельными и отражают свойства прочности испытуемого материала. (формулы 2.3…2.7). Заметим, что поучаемый в этом случае предел текучести металла соответствует новому физическому состоянию металла и поэтому называется физическим пределом текучести
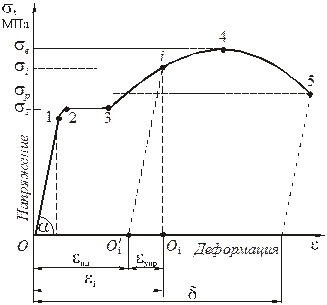 |
Рисунок. 2.4 – Диаграмма напряжений
Из диаграммы напряжений (рис. 2.4) видно, что
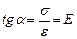 , (2.8)
, (2.8)
т. е. модуль упругости при растяжении Е численно равен тангенсу угла наклона начального прямолинейного участка диаграммы напряжений к оси абсцисс. В этом – геометрический смысл модуля упругости при растяжении.
Если относить усилия, действующие на образец в каждый момент времени нагружения, к истинному значению поперечного сечения в соответствующий момент времени, то мы получим диаграмму истинных напряжений, часто обозначаемых буквой S (рис. 2.5, сплошная линия). Поскольку на участке диаграммы 0-1-2-3-4 диаметр образца уменьшается незначительно (шейка еще не образовалась), то истинная диаграмма, в пределах этого участка, практически совпадает с условной диаграммой (пунктирная кривая), проходя несколько выше.
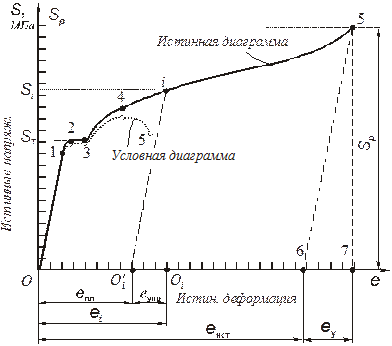
Рисунок. 2.5 – Диаграмма истинных напряжений
Построение остального участка истинной диаграммы напряжений (участок 4-5 на рис. 2.5) вызывает необходимость измерения диаметра образца в процессе испытания на растяжение, что не всегда возможно. Существует приближенный способ построения этого участка диаграммы, основанный на определении координат точки 5( 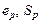 ) истинной диаграммы (рис. 2.5), соответствующей моменту разрыва образца. Сначала определяется истинное напряжение разрыва
) истинной диаграммы (рис. 2.5), соответствующей моменту разрыва образца. Сначала определяется истинное напряжение разрыва 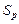
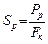 ,
,
где 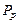 – усилие на образце в момент его разрыва;
– усилие на образце в момент его разрыва;
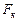 – площадь поперечного сечения в шейке образца в момент разрыва.
– площадь поперечного сечения в шейке образца в момент разрыва.
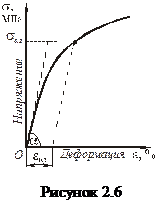 Вторая координата точки – относительная деформация
Вторая координата точки – относительная деформация 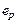 включает две составляющие – истинную пластическую –
включает две составляющие – истинную пластическую –  и упругую –
и упругую – 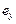 . Значение
. Значение  может быть определено из условия равенства объемов материала вблизи места разрыва образца до и после испытания (рис. 2.3). Так до испытания объем материала образца единичной длины будет равен
может быть определено из условия равенства объемов материала вблизи места разрыва образца до и после испытания (рис. 2.3). Так до испытания объем материала образца единичной длины будет равен 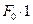 , а после разрыва
, а после разрыва 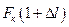 . Здесь
. Здесь 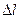 – удлинение образца единичной длины вблизи места разрыва. Поскольку истинная деформация здесь
– удлинение образца единичной длины вблизи места разрыва. Поскольку истинная деформация здесь 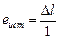 , а
, а  , то
, то  . Упругую состав--ляющую находим по закону Гука:
. Упругую состав--ляющую находим по закону Гука: 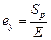 . Тогда абсцисса точки 5 будет равна
. Тогда абсцисса точки 5 будет равна 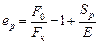 . Проводя плавную кривую между точками 4 и 5, получим полный вид истинной диаграммы.
. Проводя плавную кривую между точками 4 и 5, получим полный вид истинной диаграммы.
Для материалов, диаграмма растяжения которых на начальном участке не имеет резко выраженной площадки текучести (см. рис. 2.6 ) предел текучести условно определяют как напряжение, при котором остаточная деформация составляет величину, установленную ГОСТом или техническими условиями. По ГОСТу 1497–84 эта величина остаточной деформации составляет 0,2% измеренной длины образца, а условный предел текучестиобозначается символом –  .
.
При испытании образцов на растяжение кроме характеристик прочности определяют также характеристики пластичности, к которым относится относительное удлинение образца после разрыва 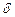 , определяемое как отношение приращения длины образца после разрыва
, определяемое как отношение приращения длины образца после разрыва 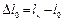 к его первоначальной длине:
к его первоначальной длине:
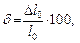 % (2.9)
% (2.9)
и относительное сужение 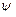 , рассчитываемое по формуле
, рассчитываемое по формуле
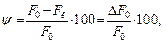 % (2.10)
% (2.10)
В этих формулах  – начальная расчетная длина и площадь поперечного сечения образца,
– начальная расчетная длина и площадь поперечного сечения образца,  – соответственно длина расчетной части и минимальная площадь поперечного сечения образца после разрыва.
– соответственно длина расчетной части и минимальная площадь поперечного сечения образца после разрыва.
Вместо относительной деформации  в некоторых случаях используют так называемую логарифмическую деформацию. Так как по мере растяжения длины образца меняется, то приращение длины dl относят не к
в некоторых случаях используют так называемую логарифмическую деформацию. Так как по мере растяжения длины образца меняется, то приращение длины dl относят не к 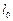 , а к текущему значению
, а к текущему значению 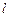 . Если проинтегрировать приращения удлинений
. Если проинтегрировать приращения удлинений  при изменении длины от
при изменении длины от 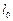 до
до 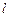 , то получим логарифмическую или истинную деформацию металла
, то получим логарифмическую или истинную деформацию металла
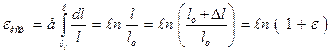 ,
,
тогда 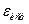 – деформация при разрыве (т.е.
– деформация при разрыве (т.е. 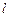 =
= 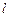 k ) будет
k ) будет
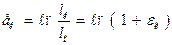 .
.
Следует еще учесть, что пластическая деформация в образце по его длине протекает неравномерно.
В зависимости от природы металла их условно подразделяют на весьма пластичные (отожженная медь, свинец) пластичные (низкоуглеродистые стали), хрупкие (серый чугун), весьма хрупкие (белый чугун, керамика).
Скорость приложения нагрузки Vдеформ влияет на вид диаграммы и характеристики материала. σТ и σв возрастает с повышением скорости нагрузки. Деформации, соответствующие пределу прочности и точке разрушения уменьшаются.
Обычные машины обеспечивают скорость деформации
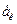 = 10-2…10-5 1/сек.
= 10-2…10-5 1/сек.
С понижением температуры Тисп у перлитных сталей увеличивается σТ и уменьшается 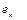 .
.
Аустенитные стали, Alи Тiсплавы слабее реагируют на понижение Т.
С ростом температуры наблюдается изменение деформаций во времени при постоянных напряжениях, т.е. протекает ползучесть, причем чем > σ , тем <  .
.
Обычно бывает три стадии ползучести. Для машиностроения наибольший интерес представляет II стадия, где έ=const (установившаяся стадия ползучести).
Для сопоставления сопротивления ползучести различных металлов введена условная характеристика – предел ползучести.
Пределом ползучести σпл называется напряжение, при котором пластическая деформация за заданный промежуток времени достигает величины, установленной техническими условиями.
Наряду с понятием “ползучести” известно еще понятие “релаксация напряжений”.
Процесс релаксации напряжений протекает при постоянных деформациях.
Образец, находящийся под постоянной нагрузкой при высокой Т может разрушиться либо с образованием шейки (вязкое интеркристаллическое разрушение), либо без нее (хрупкое транскристаллическое разрушение). Первое характерно для более низких Т и высоких σ.
Прочность материала при высоких Т оценивается пределом длительной прочности.
Пределом длительной прочности ( σдп ) называется отношение нагрузки, при которой растянутый образец через определенный промежуток времени разрушается, к первоначальной площади поперечного сечения.
При проектировании сварных изделий, работающих при повышенных Т, ориентируются на следующие величины при назначении [σ]:
а) при Т 260 оС на предел прочности σв ;
б) при Т 420 оС для углеродистых сталей Т < 470 оС для стали 12Х1МФ, Т< 550 оС для 1Х18Н10Т – на σТ ;
в) при более высоких Т на предел длительной прочности σдп .
Кроме перечисленных методов испытаний при статических нагрузках производят еще испытания на изгиб, кручение, срез, сжатие, смятие, устойчивость, твердость.
Дата добавления: 2018-11-26; просмотров: 1960;











