ВЛИЯНИЕ СООТНОШЕНИЯ АКТИВНОГО И ИНДУКТИВНОГО СОПРОТИВЛЕНИЙ

Значение 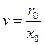, характеризующее соотношение активного и индуктивного сопротивлений линии, меняется в весьма широких пределах в зависимости от типа линии (воздушная или кабельная), ее номинального напряжения и диапазона используемых сечений проводов и жил кабелей. Систематизация и обобщение данных о величине «v» позволяют составить табл. 2.1.

Таблица 2.1

Соотношения активного и индуктивного сопротивлений линий электропередачи

Uном, кВ	6 - 10				330 - 1150
Воздушная линия   F, мм2	I категория   35 - 120	II категория	III категория
50 - 185	70 - 240	240 - 500	2x240-10x400
v, о.е.	2,2 – 0,7	1,4 – 0,4	1,0 – 0,3	0,3 – 0,15	0,18 – 0,03
Кабельная линия с медными жилами F, мм2	10 - 240	120 - 300	150 - 800	150 - 800
v, о.е	16,7 – 1,1	1,3 – 0,6	0,6 – 0,16	0,8 – 0,2
Кабельная линия с алюминиевыми жилами F, мм2	100 - 240	120 - 300	270 - 800	270 - 800
v, о.е	28,2 – 1,8	2,2 – 1,4	0,8 – 0,4	0,8 – 0,4

Анализ данных табл. 2.1 позволяет установить закономерности изменения величины v и по отношению к значению v = 1 (r₀ = x₀) выделить три категории линий:

1) линии с v ³ 1, к которым прежде всего относятся кабельные линии 6 – 10 кВ, а также 35 кВ с алюминиевыми жилами и, кроме того, частично ВЛ 6 – 35 кВ и КЛ 35 кВ с медными жилами (при небольших сечениях);

2) линии с v » 1, к которым относятся ВЛ 6 – 35 кВ и КЛ 35 кВ с медными жилами (при больших сечениях) и частично ВЛ 110 кВ;

3) линии с v £ 1, к которым относятся все воздушные и кабельные линии с U_ном ³ 110 кВ, за исключением отнесенных ко второй категории ВЛ 110 кВ.

Начнем рассмотрение со второй категории линий, которые характеризуются равенством активного и индуктивного сопротивлений линии. При этом аргумент полного сопротивления линии близок к 45⁰. Как изменится при этом векторная диаграмма напряжения (рис. 2.6,а), соответствующая режиму максимальной нагрузки линии?

Чтобы ответить на этот вопрос, вновь вернемся к выражению (2.14а) для вектора падения напряжения и сгруппируем в нем попарно составляющие, определяемые активной и реактивной составляющими тока I_1,2, т.е.

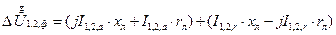. (2.17)

Первые два слагаемые являются катетами треугольника, гипотенузой которого является вектор 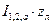, т.е. этот треугольник определяется протеканием в продольной ветви схемы замещения активной мощности Р_1,2, причем при рассматриваемом соотношении r_л и x_л вектор 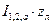расположен под углом » 45⁰ к действительной оси комплексной плоскости.

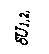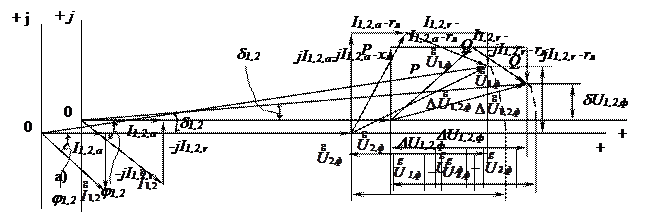Рис. 2.9. Векторные диаграммы токов и напряжений линии при r_л = x_л (а) и при r_л = 0,5х_л (б)

Построим этот треугольник на векторной диаграмме (рис. 2.9,а), пометив его символом «Р».

Последние два слагаемых в (2.17) являются катетами треугольника с гипотенузой 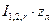и определяются протеканием через сопротивления линии реактивной мощности Q_1,2. При примерном равенстве r_л » x_л вектор 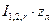направлен под углом «- 45⁰» к действительной оси комплексной плоскости. Изобразим этот треугольник на рис. 2.9,а и отметим его символом «Q». Очевидно, что размеры треугольников определяются соотношением Р_1,2 и Q_1,2, причем в соответствии с рис. 2.6,а имеем I_1,2,r < I_1,2,a.

В результате построения этих треугольников получаем вектор 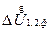, который в рассматриваемом случае имеет относительно малую поперечную составляющую. Это, в свою очередь, приводит к тому, что фазовый сдвиг между 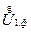и 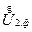(< d_1,2) также невелик. При этом, если пренебречь поперечной составляющей вектора падения напряжения, то

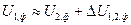(2.18а)

и аналогично для линейных напряжений

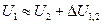. (2.18б)

Разность модулей векторов напряжений по концам линии, как мы уже отмечали ранее, называется потерей напряжения.Именно величина потери напряжения от шин источника питания до шин узла нагрузки в ряде случаев служит критерием допустимости рассматриваемого режима с позиции обеспечения качества электроэнергии, получаемой потребителем, и поэтому является важным качественным показателем работы сети. В рассматриваемом случае потеря напряжения

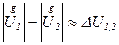, (2.19)

т.е. примерно равна продольной составляющей вектора падения напряжения.

Нетрудно убедиться, что сказанное ранее тем более справедливо для линий первой категории, где r_л ³ x_л. Отсюда следует важное практическое обобщение: расчет напряжений в узлах электрических сетей с U_ном £ 110 кВ допустимо выполнять без учета поперечной составляющей вектора падения напряжения, т.е. считая узловые напряжения вещественными числами и принимая потерю напряжения на каждом участке сети равной продольной составляющей вектора падения напряжения. Расчет установившегося режима сети при этом существенно упрощается, а возникающая погрешность, как правило, лежит в пределах точности задания исходных данных.

Иная ситуация имеет место при рассмотрении линий третьей категории, для которых справедливо соотношение r_л < x_л . Соответствующая этому случаю векторная диаграмма приведена на рис. 2.9б. Из анализа диаграммы следует, что при r_л < x_л поперечная составляющая вектора падения напряжения и угол сдвига напряжений по концам линии или угол между 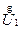и 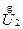(< d_1,2) значительны, причем они тем больше, чем больше различие между r_л и x_л. Отсюда вывод: расчет напряжений в узлах электрических сетей с U_ном ³ 220 кВ в общем случае недопустимо выполнять без учета поперечной составляющей вектора падения напряжения.

При этом напряжение каждого узла характеризуется модулем и фазой, отсчитываемой от вектора напряжения узла, принятого за базовый.