ПАДЕНИЕ И ПОТЕРЯ НАПРЯЖЕНИЯ В ЛИНИИ

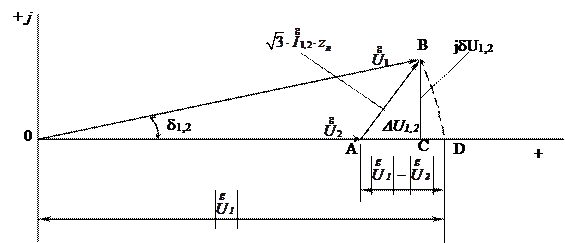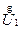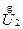Рассмотрим векторную диаграмму для линейных напряжений в начале и в конце линии и . Очевидно, что эта векторная диаграмма подобна диаграмме для фазных напряжений в начале и в конце лини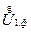и и 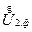, рассмотренной ранее

Рис. 2.8. К оценке падения и потери напряжения в линии

Падение напряжения –геометрическая (векторная) разность между комплексами напряжений начала и конца линии. На рис. 2.8 падение напряжения – это вектор 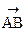, т.е.

.

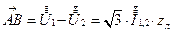Продольной составляющей падения напряжения DU_1,2 называют проекцию падения напряжения на действительную ось или на напряжение 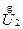, т.е. величину DU_1,2 = АС на рис. 2.8. Обычно DU_1,2 выражается через известные в конце линии значения , , .

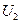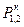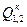Поперечная составляющая падения напряжения dU_1,2 – это проекция падения напряжения на мнимую ось, dU_1,2 = СВ на рис. 2.8. Таким образом,

.

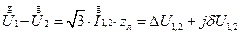Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала и конца линии.

На рис. 2.8 определено 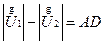. Если поперечная составляющая падения напряжения dU_1,2 мала (например, в сетях U_ном £ 110 кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения.

Расчет режимов электрических сетей ведется в мощностях. Поэтому падения напряжения в целом и его составляющие принято выражать через потоки мощности в линии.