Сечения ядерных реакций
Факт ядерной реакции, как и все процессы в микромире, является случайным явлением. Поэтому для количественного описания возможности ядерной реакции необходимо использовать вероятностный подход. Такой количественной характеристикой вероятности протекания ядерной реакции является эффективное сечение, которое определяется следующим образом. Пусть на площадку S = 1 см2 тонкой пластинки, содержащей ядра-мишени А, падает перпендикулярно однородный в пределах площадки поток 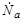 - количество частиц а в единицу времени. Тонкой будем считать пластинку, в которой ядра А не затеняют друг друга. Оценим толщину пластинки. Так как размеры ядер меньше размеров атомов примерно в 104 раз, то соответствующие им площади будут различаться в 108 раз. В твердом теле атомы упакованы плотно, поэтому необходимо 108 слоев атомов для заметного перекрытия ядер А друг другом. Принимая диаметр одного атома примерно равным 10-8 см, получим, что толщина δ пластинки составит ~1 см. В слое dx << δ затенением ядер-мишеней можно пренебречь и возможное число реакций в 1 см2 пластинки
- количество частиц а в единицу времени. Тонкой будем считать пластинку, в которой ядра А не затеняют друг друга. Оценим толщину пластинки. Так как размеры ядер меньше размеров атомов примерно в 104 раз, то соответствующие им площади будут различаться в 108 раз. В твердом теле атомы упакованы плотно, поэтому необходимо 108 слоев атомов для заметного перекрытия ядер А друг другом. Принимая диаметр одного атома примерно равным 10-8 см, получим, что толщина δ пластинки составит ~1 см. В слое dx << δ затенением ядер-мишеней можно пренебречь и возможное число реакций в 1 см2 пластинки
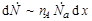 , ,
| (4.3.1) |
где nА – концентрация ядер-мишеней А. Из (4.3.1) следует, что вероятность (доля) реакций составит
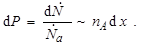
| (4.3.2) |
Запишем (4.3.2) в виде точного равенства:
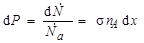 , ,
| (4.3.3) |
где σ – коэффициент пропорциональности, имеющий размерность площади, называется эффективным (микроскопическим) сечением ядерной реакции. В общем случае эффективное сечение зависит от кинетической энергии Та частиц а, т.е. 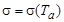 .
.
Формулу (4.3.3) можно представить в виде
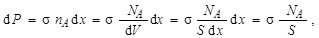
| (4.3.4) |
где dV – объем слоя dx, а NA – число ядер А в этом слое. Выражение (4.3.4) есть ничто иное, как отношение эффективной площади всех ядер в пластинке, к площади S пластинки толщиной 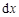 . Поэтому эффективное сечение есть среднее значение площади, при нахождении в пределах которой частиц а и А с определенной вероятностью должна произойти реакция, если последние считать точками. В ядерной физике для измерения сечений используется специальная единица, называемая барн (б), 1б = 10-24 см2.
. Поэтому эффективное сечение есть среднее значение площади, при нахождении в пределах которой частиц а и А с определенной вероятностью должна произойти реакция, если последние считать точками. В ядерной физике для измерения сечений используется специальная единица, называемая барн (б), 1б = 10-24 см2.
Часто используется также величина макроскопического сечения
| S = nАs, | (4.3.5) |
имеющей размерность длины. Физический смысл этой величины раскрывается ниже.
Перепишем (4.3.3) в виде
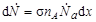
| (4.3.6) |
и разделим левую и правую части равенства (4.3.6) на бесконечно малый объем dV = Sdx. В результате получим
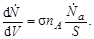
| (4.3.7) |
 В ядерной физике оказалось удобным использовать величину плотности потока частиц Ф, определяющую интенсивность поступления частиц в заданный объем. Пусть в объем сферы (рис. 4.3.1) с площадью поперечного сечения S по всевозможным направлениям поступает однородный в пределах объема сферы поток частиц
В ядерной физике оказалось удобным использовать величину плотности потока частиц Ф, определяющую интенсивность поступления частиц в заданный объем. Пусть в объем сферы (рис. 4.3.1) с площадью поперечного сечения S по всевозможным направлениям поступает однородный в пределах объема сферы поток частиц 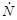 . Тогда по определению плотность потока частиц а равна
. Тогда по определению плотность потока частиц а равна
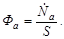
| (4.3.8) |
Обозначим через 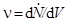 - число реакций, происходящих в бесконечно малом объеме вещества мишени в единицу времени. С учетом этого и (4.3.8) выражение (4.3.7) принимает вид
- число реакций, происходящих в бесконечно малом объеме вещества мишени в единицу времени. С учетом этого и (4.3.8) выражение (4.3.7) принимает вид
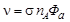 , ,
| (4.3.9) |
где Фа – плотность потока частиц а. Выражение (4.3.9) будет в дальнейшем неоднократно использоваться.
Установим, как изменяется плотность потока частиц а при их движении в пластинке. Число реакций в единицу времени, происходящих в тонком слое мишени единичной площади и толщиной dx, равно ndx,а с другой стороны равно убыванию плотности потока частиц в этом слое, то есть
| ndx = - dФа. | (4.3.10) |
Используя (4.3.9) и (4.3.10) получаем дифференциальное уравнение для ослабления плотности потока частиц а:
| dФа= - snАФаdx, | (4.3.11) |
которое следует интегрировать с граничным условием Фа(х = 0) = Ф0. Сечение s также является функцией х, так в общем случае энергия частиц является функцией прйденного в мишени расстояния, но часто (например, в случае прохождения тепловых нейтронов через вещество) можно приближенно считать, что s не зависит от x. Тогда, разделяя переменные в (4.3.11), получим после интегрирования:
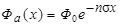 = =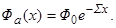
| (4.3.12) |
Из (4.3.12) получаем вероятность частице a пройти без столкновений путь x:
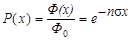 = =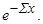
| (4.3.13) |
Найдем среднюю длину пробега частиц а до первого взаимодействия:
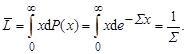
| (4.3.14) |
 Таким образом, макроскопическое сечение S [см-1] имеет смысл среднего числа взаимодействий частиц а c ядрами А на единице длины пути в мишени, то есть смысл коэффициента поглощениявматериале мишени.
Таким образом, макроскопическое сечение S [см-1] имеет смысл среднего числа взаимодействий частиц а c ядрами А на единице длины пути в мишени, то есть смысл коэффициента поглощениявматериале мишени.
Более подробной характеристикой ядерного взаимодействия (реакции или рассеяния) служит дифференциальное сечение:
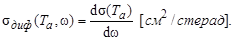
| (4.3.15) |
Дифференциальное сечение определяет плотность вероятности продуктам (В или b) реакции (4.1.1) вылететь в пределах телесного угла 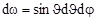 в направлении
в направлении 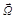 (рис. 4.3.2). Дифференцируя (4.3.3) по ω, получим выражение
(рис. 4.3.2). Дифференцируя (4.3.3) по ω, получим выражение
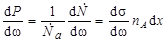 , ,
| (4.3.16) |
которое устанавливает связь между дифференциальным сечением и плотностью вероятности.
Если спины налетающих частиц и ядер в мишени ориентированы хаотично, то процесс взаимодействия обладает цилиндрической симметрией относительно оси, совпадающей с направлением движения частицы a , т.е. не зависит от полярного угла φ и определяется только азимутальным углом 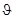 вылета одной из частиц.
вылета одной из частиц.
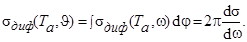
| (4.3.17) |
Зависимость дифференциального сечения от угла вылета 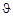 называется угловым распределением.
называется угловым распределением.
Интегрирование (4.3.17) по углу 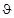 устанавливает связь между эффективным сечением и угловым распределением:
устанавливает связь между эффективным сечением и угловым распределением:
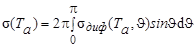
| (4.3.18) |
Часто вместо зависимости 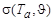 используют зависимость s(Та,m), где m º cos
используют зависимость s(Та,m), где m º cos 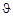 . Тогда
. Тогда
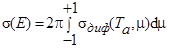 . .
| (4.3.19) |
На одних и тех же ядрах А под действием частиц а могут иметь место различные выходные каналы (см. (4.1.2)), каждый из которых характеризуется своим парциальными микроскопическим σi и макроскопическим Σi сечениями. Тогда, в соответствие с (4.3.6), сечения входного канала или полные сечения st и Σt складываются из парциальных сечений следующим образом:
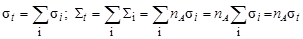 . .
| (4.3.20) |
Если же вещество мишени имеет в своем составе ряд различных нуклидов, концентрация ядер каждого из которых равна nj, то в этом случае можно говорить только о полном макроскопическом сечении
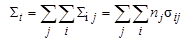 , ,
| (4.3.21) |
где 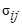 - микроскопическое сечение реакции вида i на ядрах j, или же о средней (приходящейся на одно ядро) величине микроскопического сечения реакции вида i:
- микроскопическое сечение реакции вида i на ядрах j, или же о средней (приходящейся на одно ядро) величине микроскопического сечения реакции вида i:
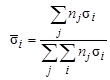 . .
| (4.3.22) |
Используя (4.3.14) и (4.3.20) или (4.3.21) можно рассчитать полную среднюю длину пробега 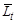 частиц а:
частиц а:
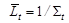 , ,
| (4.3.23) |
Вероятность осуществления ядерной реакции, непосредственно измеряемая в физических экспериментах и позволяющая экспериментально определить макроскопическое сечение, есть выход ядерной реакции Y или просто выход. Выход определяется как среднее число частиц а, испытавших взаимодействие в единицу времени, отнесенное к полному числу частиц а, падающих на мишень макроскопических размеров в единицу времени. Вид формулы, связывающей выход и макроскопическое сечение, определяется конкретным видом ядерной реакции. Для примера рассмотрим процесс (4.3.12) на мишени толщиной d:
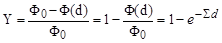 . .
| (4.3.24) |
После небольших преобразований и логарифмирования получаем формулу для нахождения макроскопического сечения
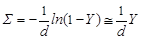 , ,
| (4.3.25) |
если, как обычно, Y << 1.
Для экспериментального определения дифференциального сечения необходимо измерить угловое распределение продуктов реакции или рассеяния частиц а
Дата добавления: 2021-07-22; просмотров: 716;











