Теория течения с трансляционным упрочнением

Чтобы отразить наклеп, достаточно считать величину s_T­ зависящей от 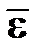, 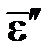или λ. Но чтобы отразить эффект Баушингера, нужно считать пределы текучести при растяжении и сжатии различающимися: когда один из них растет, второй должен убывать. Проще всего этого добиться разделением напряжения на два слагаемых:

,

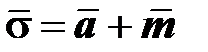где 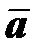– активное, а 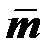– дополнительное напряжение. Неупругое деформирование связывают с активным напряжением 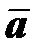. Например, аналогично теории идеальной пластичности запишем

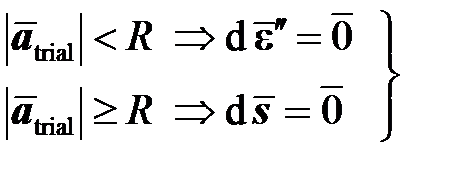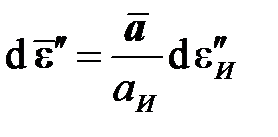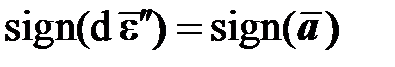, , . (8.1)

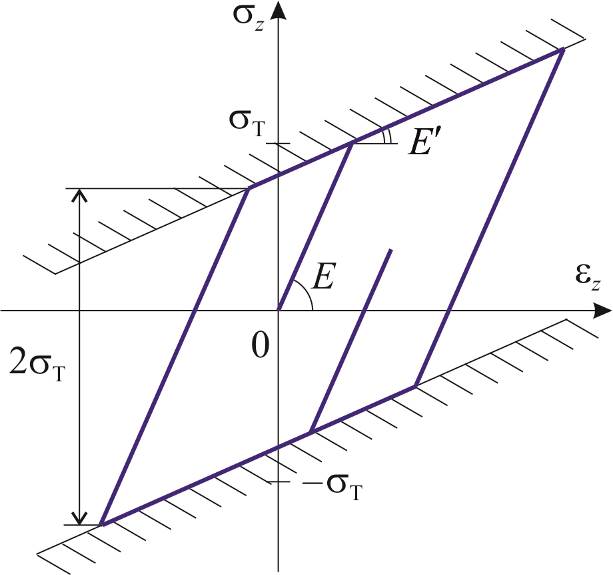
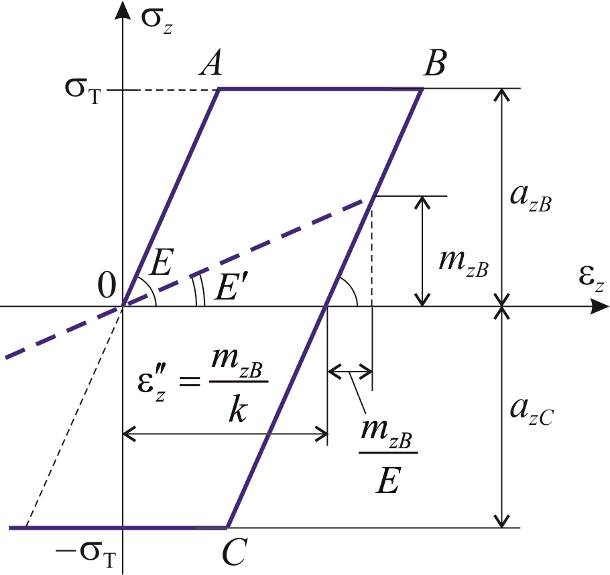
а)	б)
Рис.8.1

Параметр 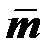рассматривается как скрытый параметр состояния, связанный с историей неупругой деформации. Простейший вариант такой зависимости

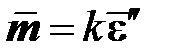(8.2)

вместе с уравнениями (8.1) определяет теорию течения с трансляционным упрочнением – теорию Ишлинского-Прагера. Трансляционное упрочнение является анизотропным с точки зрения знака нагружения, его также называют кинематическим. Диаграмма деформирования при одноосном растяжении (рис.8.1), описываемая этой теорией, состоит из двух участков: упругого, где

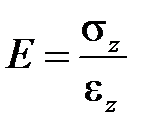
и участка линейного упрочнения, где

.

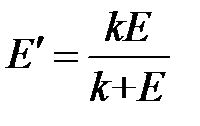При нагрузке и нагружении обратного знака из любой точки на втором участке диаграмма опять будет состоять из двух участков с такими же наклонами, причем протяженность упругого участка всегда одинакова: по оси напряжений она отвечает изменению 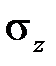на 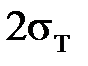. Это означает, что наклеп (превышение начального предела текучести) на 50 МПа соответствует разупрочнению при нагружении обратного знака на те же 50 МПа (идеальный эффект Баушингера). Точка B на рис.8.1 соответствует упрочнению, а точка C ­ разупрочнению. Напряжения в этих точках равны соответственно

, ,

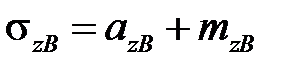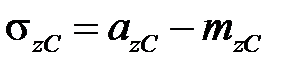где 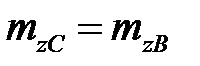. Циклического (изотропного) упрочнения такая модель не отражает: петля пластического гистерезиса во всех циклах имеет одинаковую форму с теми же двумя участками.