Теория идеальной пластичности при сложном нагружении
Теория идеальной пластичности основана на том, что выход за поверхность текучести невозможен: девиатор напряжений может лишь находиться внутри или скользить по поверхности текучести. Если вектор
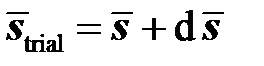
выходит за поверхность текучести, то происходит такое изменение пластической деформации 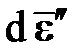 , что вектор
, что вектор 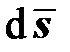 лежит на поверхности текучести, то есть девиатор напряжений
лежит на поверхности текучести, то есть девиатор напряжений 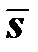 , а также девиатор упругой деформации
, а также девиатор упругой деформации 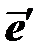 скользит по границе упругой области, а пластическая деформация при этом накапливается. В противном случае изменения пластической деформации не происходит. Это можно записать с помощью следующих уравнений:
скользит по границе упругой области, а пластическая деформация при этом накапливается. В противном случае изменения пластической деформации не происходит. Это можно записать с помощью следующих уравнений:
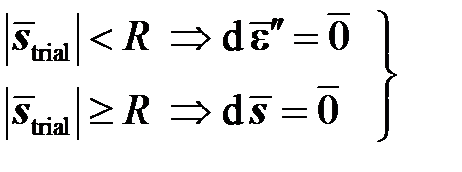 . (6.1)
. (6.1)
Накопление пластической деформации происходит в соответствии с ассоциированным законом пластического течения, что позволяет записать следующее:
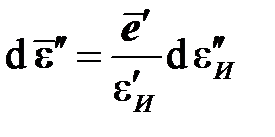 ,
, 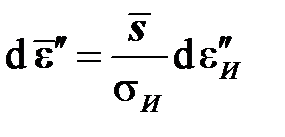 . (6.2)
. (6.2)
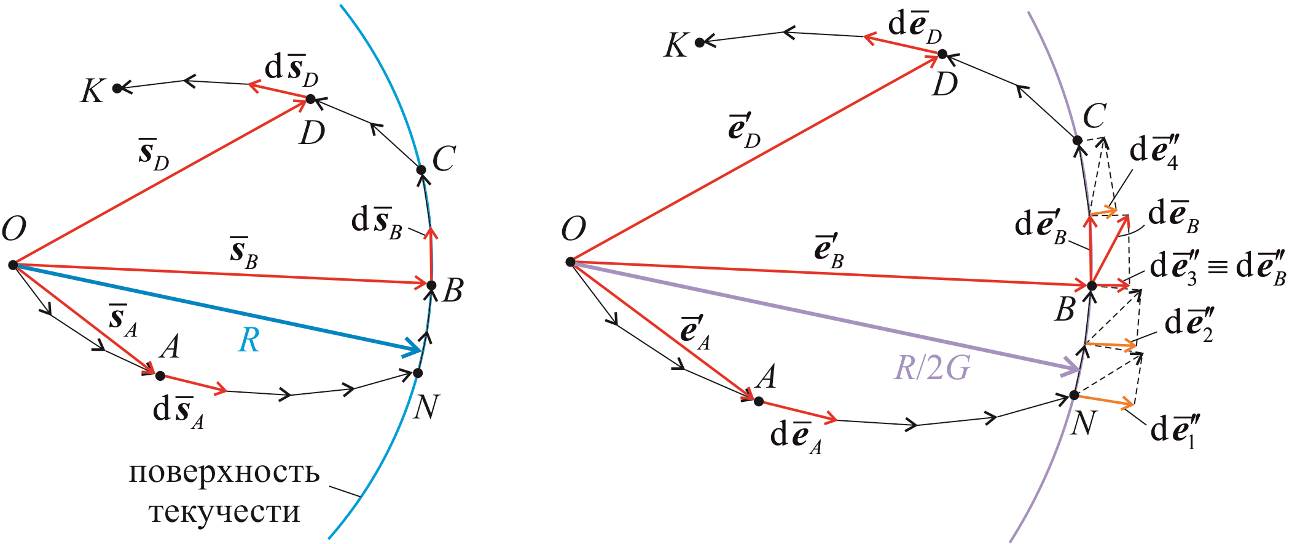
На рис.6.1 показана некоторая траектория ONCK деформирования идеально пластичного материала из начального состояния, соответствующего точке O, до некоторого текущего состояния (точка K). На участке ON, то есть до того момента, когда вектор упругой деформации достиг поверхности текучести, материал деформируется линейно упруго. Девиатор деформаций в произвольной точке A этого участка совпадает с его упругой составляющей (она возрастает), а пластической составляющей деформации пока нет
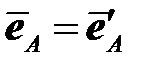 ,
, 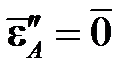 .
.
|
| Рис.6.1 |
На участке NC происходит рост пластической деформации, упругая составляющая при этом не меняется. Например, приращение девиатора деформации 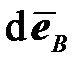 в точке B пытается вывести упругую деформацию
в точке B пытается вывести упругую деформацию 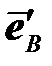 за упругую область
за упругую область 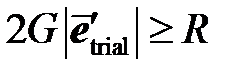 . Приращение девиатора деформации при этом раскладывается на две составляющие, ортогональных друг другу (ортогональность следует из ассоциированного закона пластического течения): упругую
. Приращение девиатора деформации при этом раскладывается на две составляющие, ортогональных друг другу (ортогональность следует из ассоциированного закона пластического течения): упругую 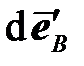 и пластическую
и пластическую 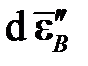 . В точках N, B и C векторы пластических деформаций, естественно, отличаются друг от друга, возрастая от точки N к точке C:
. В точках N, B и C векторы пластических деформаций, естественно, отличаются друг от друга, возрастая от точки N к точке C:
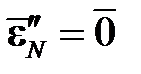 ,
, 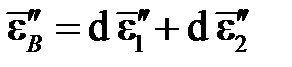 ,
, 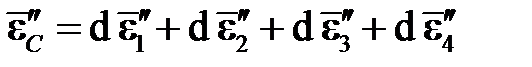 .
.
Вместе с пластической составляющей при этом растет и полная деформация. На участке CK пластическая составляющая деформации остается неизменной и равной накопленной к точке C деформации 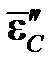 , а упругая деформация снижается от точки C до точки K. Например, в точке D пластическая деформация и девиатор деформации равны соответственно:
, а упругая деформация снижается от точки C до точки K. Например, в точке D пластическая деформация и девиатор деформации равны соответственно:
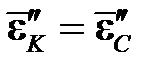 ,
, 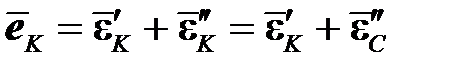 .
.
Дата добавления: 2017-06-13; просмотров: 1645;











