Модель идеальной пластичности при одноосном растяжении
|
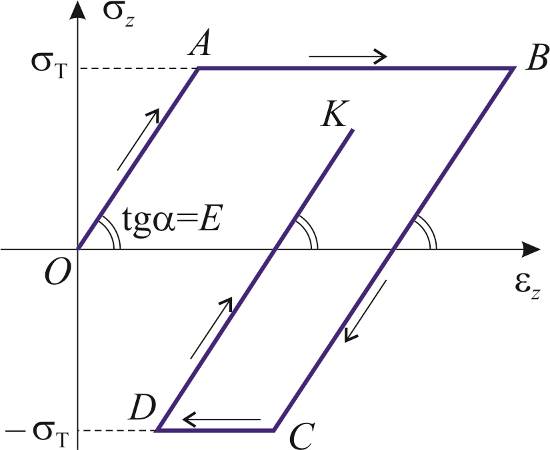
| Рис.4.1 |
Простейшей моделью неупругого склерономного тела является модель идеально пластического материала. При одноосном нагружении она характеризуется диаграммой Прандтля: при напряжениях, не превышающих по модулю предела текучести, оно деформируется упруго (при этом приращение пластической деформации равно нулю); при s = sT происходит рост пластической деформации, а при s = –sT – убывание. При пластическом деформировании напряжение постоянно. Последняя особенность приводит к тому, что идеально пластический материал граничит с неустойчивым материалом, его нагружение не может быть чисто силовым: реакция в этом случае неоднозначна. Но при кинематическом воздействии идеально пластическое тело вполне устойчиво, его реакция однозначна. Для примера на рис.4.1 показана диаграмма деформирования OABCDK при некоторой заданной истории деформации.
Математически поведение идеально пластического материала описывается выражением
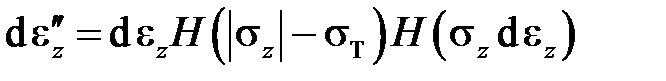 . (4.1)
. (4.1)
десь H(x) – это функция Хевисайда, равная 0 при x < 0 и равная 1 при x ³ 0. Данное выражение точно отражает поведение идеально пластического материала при кинематическом нагружении, но нужно иметь незаурядный опыт, чтобы его «прочитать», то есть отчетливо представить и понять смысл записанного. На участках OA, BC и DK приращение пластической деформации 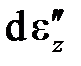 равно нулю, за что отвечает второй множитель этого выражения
равно нулю, за что отвечает второй множитель этого выражения 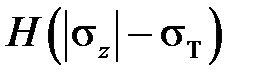 . На участке OA пластическая деформация возрастает и ее приращение совпадает с приращением полной деформации. За возрастание пластической деформации отвечает третий множитель этого выражения
. На участке OA пластическая деформация возрастает и ее приращение совпадает с приращением полной деформации. За возрастание пластической деформации отвечает третий множитель этого выражения 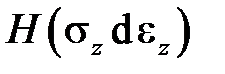 , а за совпадение с полной деформацией – первый множитель
, а за совпадение с полной деформацией – первый множитель 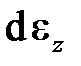 . На участке CD та же ситуация, только с противоположным знаком – пластическая деформация на этом участке убывает.
. На участке CD та же ситуация, только с противоположным знаком – пластическая деформация на этом участке убывает.
|
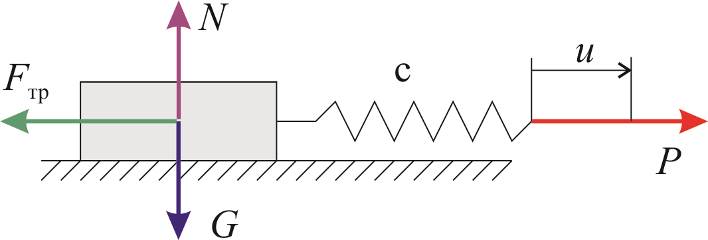
| Рис.4.2 |
Существует простая и значительно более наглядная механическая аналогия, описываемая выражением того же типа (рис.4.2). Некоторый груз лежит на столе и может приводиться в движение с помощью пружины жесткостью с, если сила P достигнет предельного значения силы трения Fтр. При |P| < Fтр груз неподвижен, и смещение u связано с деформированием пружины. При |P| = Fтр груз сдвигается; силами инерции пренебрегаем, потому в процессе движения груза сила постоянна и равна Fтр. Связь между u и P описывается выражением (4.1), если заменить напряжение sz на силу P, продольную деформацию ez на перемещение u точки приложения силы, а перемещение груза 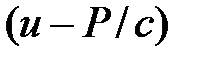 – на пластическую деформацию
– на пластическую деформацию 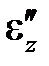 .
.
Дата добавления: 2017-06-13; просмотров: 1720;











