Теория течения с изотропным упрочнением

Основной недостаток модели идеально пластичного материала – это весьма упрощенная схематизация диаграмма деформирования. Простейший путь для устранения этого недостатка – сделать величину s_T переменной, возрастающей по мере деформирования. Например, можно положить s_T функцией деформации: в процессе деформирования при растяжении она возрастает. Однако при сжатии s_T будет уменьшаться, как и деформация. При этом нарушается постулат устойчивости Друкера (ds_z de_z > 0), что не соответствует реальному поведению материалов. Логично использовать неубывающий параметр – параметр Удквиста λ, представляющий путь пластической деформации

.

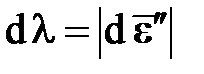В отличие от пластической деформации, параметр Удквиста – это скрытый параметр состояния, показывающий суммарную степень пластического деформирования за всю историю деформирования независимо от того, происходит растяжение, сжатие или циклическое неупругое деформирование. Функция

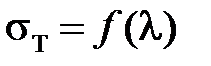, (7.1)

где предел текучести определяется параметром Удквиста, представляет собой уравнение состояния теории течения с изотропным упрочнением. Отметим, что пластическая деформация металла в теории течения уподобляется течению вязкой жидкости. В случае сложного нагружения параметр Удквиста в уравнении состояния определяет не предел текучести s_T, а функцию поверхности текучести 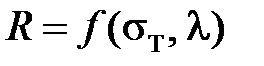и представляет собой интенсивность приращения неупругой деформации

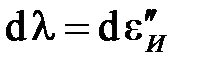. (7.2)

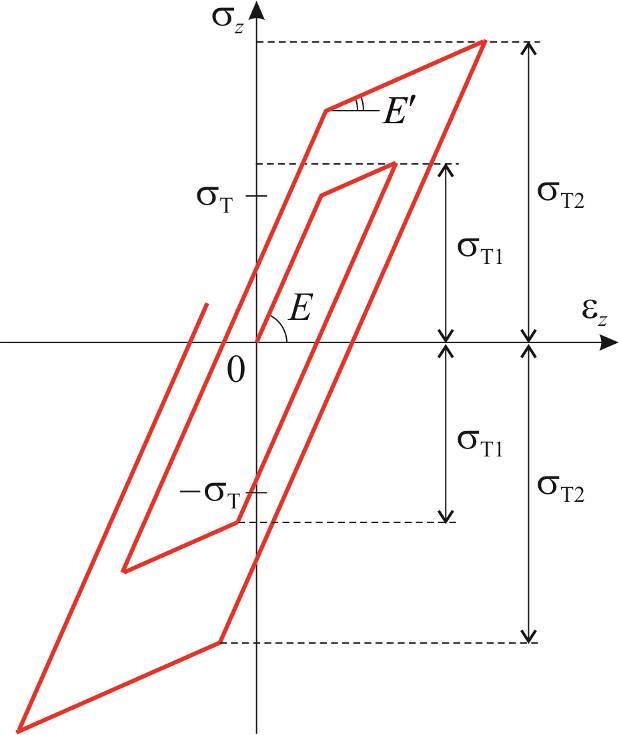
Рис.7.1

В остальном уравнения модели остаются теми же, что и у идеально пластичного материала:

,

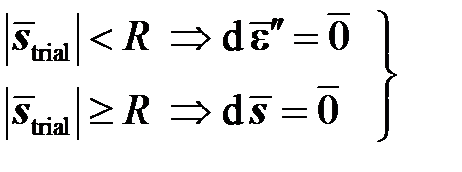а накопление пластической деформации также происходит в соответствии с ассоциированным законом пластического течения:

, .

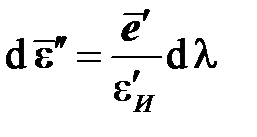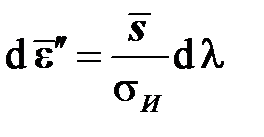Поскольку λ не убывает, s_T(λ) одинаково лимитирует область упругой работы в сторону растяжения и сжатия, описываемое упрочнение является изотропным, то есть одинаковым для напряжений любого знака. Диаграмма растяжения при этом может быть описана практически с любой точностью подбором зависимости (7.1), но при разгрузке после достижения некоторого λ = λ₁, при котором s_T = s_T1, материал работает упруго в диапазоне напряжений от (–s_T1) до s_T1. Аналогично, после достижения λ = λ₂, при котором s_T = s_T2, материал работает упруго в диапазоне напряжений от (–s_T2) до s_T2 и так далее. Это противоречит экспериментальным наблюдениям: в действительности наклеп, связанный с ростом s_T при растяжении, не означает роста предела текучести при сжатии. Наоборот, обычно обнаруживается разупрочнение (снижение предела текучести) при наклепе нагружением другого знака. Упрочнение всегда анизотропно, то есть различно по отношению к растяжению и сжатию.

Функцию (7.1) можно подобрать так, чтобы верно отразить процесс циклического упрочнения в испытаниях с заданной амплитудой внешнего воздействия. Тогда величина s_T должна заметно медленнее повышаться с ростом λ от полуцикла к полуциклу, чем это необходимо для описания начальной кривой деформирования: путь циклического пластического деформирования до стабилизации может быть на порядки большим, чем при однократном нагружении до выхода на предельное напряжение. Но тогда диаграммы деформирования в каждом цикле будут практически соответствовать диаграмме Прандтля.

Иногда для описания циклического упрочнения вместо параметра λ используют номер полуцикла k = 2N, 2N + 1 (где N – это номер цикла нагружение). В отличие от параметра Удквиста эта величина не связана с размахом деформаций в цикле, то есть упрочнение перестает зависеть от каких-либо характеристик цикла. Если принять

,

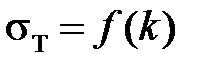Диаграммы в каждом полуцикле будут диаграммами Прандтля, но с возрастающим при увеличении числа полуциклов пределом текучести. Эксперименты показывают, что в действительности изотропное упрочнение зависит от амплитуды: при практически упругом циклическом нагружении упрочнения почти не происходит, хотя номер цикла возрастает.