Временные параметры сетевых графиков
Параметры событий:
• ранний (ожидаемый) срок tp(i) свершения i-го события определяется продолжительностью максимального пути, предшествующего этому событию: 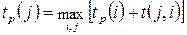 ;
;
• поздний (предельный) срок tп(i) свершения i-го события равен: 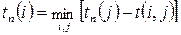 ;
;
• резерв времени R(i) i-го события определяется как разность между поздним и ранним сроками его свершения: 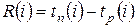 .
.
Резерв времени показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ. Ранний срок наступления завершающего события сети равен длине критического пути. Критические события резервов времени не имеют. События с нулевыми резервами времени определяют топологию критического пути.
Параметры работ:
• ранний срок tрн(i,j) начала работы (i,j) совпадает с ранним сроком наступления начального (предшествующего) события i :
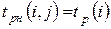 ;
;
• ранний срок tро(i,j) окончания работы (i,j) определяется по формуле:
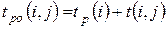 ;
;
• поздний срок tпо(i,j) окончания работы (i,j) совпадает с поздним сроком конечного события:
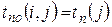 ;
;
• поздний срок tпн(i,j) начала работы (i,j) определяется по формуле:
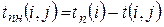 .
.
Резерв времени пути R(L) определяется как разность между длиной критического и рассматриваемого пути: R(L)=tкр – t(L).
Полный резерв времени Rп (i,j) работы (i,j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится:
Rп(i,j) = tп(j) – tp(i) – t(i,j).
Ø Важно помнить.Работы, лежащие на критическом пути, резервов не имеют.
Пример решения задачи. Для заданного сетевого графика рассчитать все параметры событий и работ, определить критический путь и его длину.
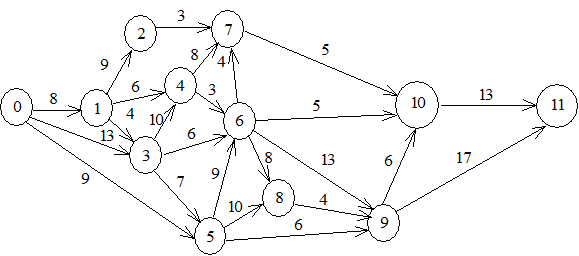
Рис. 3.2. Сетевой график
Расчет временных параметров событий удобно представить в таблице.
Таблица 3.1
Параметры событий сетевого графика
| Номер события | ||||||||||||
| Ранний срок tр(i) | ||||||||||||
| Поздний срок tп(i) | ||||||||||||
| Резерв времени R(i) |
Критический путь образуют следующие события:
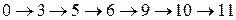 . Топологию критического пути определяют события, резерв времени которых равен нулю. Его продолжительность составляет 61 день (ранний срок свершения последнего события).
. Топологию критического пути определяют события, резерв времени которых равен нулю. Его продолжительность составляет 61 день (ранний срок свершения последнего события).
Для определения временных параметров работ также используем таблицу, в которую сведем результаты вычислений. Расчеты проводим с помощью приведенных выше формул.
Таблица 3.2
Параметры работ сетевого графика
| № | Работа (i,j) | Продолжитель-ность работы (i,j) | Сроки начала и окончания работы | Резерв времени Rп(i,j) | |||
| tрн(i,j) | tро(i,j) | tпн(i,j) | tпо(i,j) | ||||
| (0, 1) | |||||||
| (0, 3) | |||||||
| (0, 5) | |||||||
| (1, 2) | |||||||
| (1, 4) | |||||||
| (1, 3) | |||||||
| (2, 7) | |||||||
| (3, 4) | |||||||
| (3, 5) | |||||||
| (3, 6) | |||||||
| (4, 7) | |||||||
| (4, 6) | |||||||
| (5, 6) | |||||||
| (5, 8) | |||||||
| (5, 9) | |||||||
| (6, 7) | |||||||
| Продолжение таблицы 3.2 | |||||||
| (6, 10) | |||||||
| (6, 9) | |||||||
| (6, 8) | |||||||
| (7, 10) | |||||||
| (8, 9) | |||||||
| (9, 10) | |||||||
| (9, 11) | |||||||
| (10, 11) |
3.4. Сетевое планирование в условиях неопределенности
При определении временных параметров сетевой модели до сих пор предполагалось, что время выполнения каждой работы точно известно. На практике, чаще всего, продолжительность работы по сетевому графику заранее неизвестна и может принимать лишь одно из ряда возможных значений. То есть продолжительность работы t(i,j) является случайной величиной, характеризующейся своими числовыми характеристиками – средним значением (математическим ожиданием) 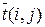 и дисперсией
и дисперсией 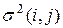 . Для определения этих числовых характеристик на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки:
. Для определения этих числовых характеристик на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки:
a) оптимистическую оценку 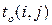 , то есть продолжительность работы (i,j) при самых благоприятных условиях;
, то есть продолжительность работы (i,j) при самых благоприятных условиях;
b) пессимистическую оценку 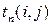 , то есть продолжительность работы (i,j) при самых неблагоприятных условиях;
, то есть продолжительность работы (i,j) при самых неблагоприятных условиях;
c) наиболее вероятную оценку 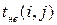 , то есть продолжительность работы (i,j) при нормальных условиях.
, то есть продолжительность работы (i,j) при нормальных условиях.
На основании этих временных оценок вычисляем числовые характеристики:
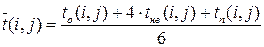 ,
, 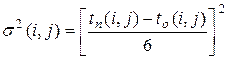 ,
,
или упрощенная (и менее точная) формула
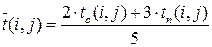 .
.
Зная 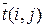 и
и 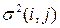 , можно определить все временные параметры сетевого графика, так же как и в случае с фиксированными продолжительностями работ, но теперь эти параметры будут являться средними значениями соответствующих случайных величин. Поэтому предварительный анализ сетей со случайными продолжительностями работ, как правило, не ограничивается расчетами временных параметров. Очень важным моментом анализа становится оценка вероятности того, что срок выполнения проекта tкр не превзойдет заданного директивного срока Т.
, можно определить все временные параметры сетевого графика, так же как и в случае с фиксированными продолжительностями работ, но теперь эти параметры будут являться средними значениями соответствующих случайных величин. Поэтому предварительный анализ сетей со случайными продолжительностями работ, как правило, не ограничивается расчетами временных параметров. Очень важным моментом анализа становится оценка вероятности того, что срок выполнения проекта tкр не превзойдет заданного директивного срока Т.
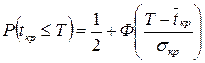 ,
,
где Ф(х) – функция Лапласа, ее значения табулированы, эта функция нечетная, то есть Ф(–х) = – Ф(х); 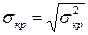 – среднее квадратическое отклонение длины критического пути.
– среднее квадратическое отклонение длины критического пути.
В некоторых случаях представляет интерес решение обратной задачи: определение максимального срока выполнения проекта Т, который возможен с заданной надежностью (вероятностью) β. В этом случае необходимо применить формулу
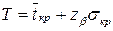 , где
, где 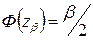 .
.
Пример решения задачи. Для заданного ранее сетевого графика определить вероятность того, что проект будет выполнен в срок Т = 63 суткам, если 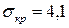 . Оценить максимально возможный срок Т выполнения проекта с надежностью β=0,95.
. Оценить максимально возможный срок Т выполнения проекта с надежностью β=0,95.
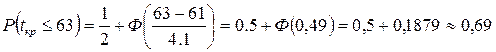 ,
,
то есть с вероятностью 0,69 проект будет выполнен за 63 дня.
Для обратной задачи:
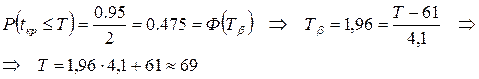
То есть с надежностью 0,95 срок выполнения проекта не превысит 69 суток.
Дата добавления: 2020-10-14; просмотров: 1069;











