Дифференциальные уравнения. Общее и частное решение дифференциальных уравнений. Уравнения с разделяющимися переменными.
Изучению этой темы предшествуют разделы «Дифференциальное исчисление» и «Интегральное исчисление».
Вспомогательные материалы:
Основные соотношения:
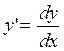
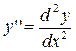
Таблица интегралов
1. 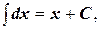
2. 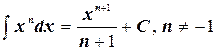
3. 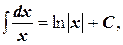
4. 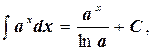
5. 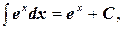
6. 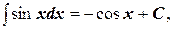
7. 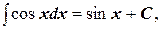
8. 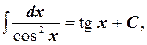
9. 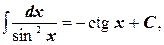
10. 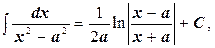
11. 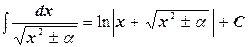
12. 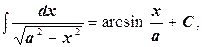
13. 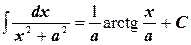 ,
,
Свойства интегралов:
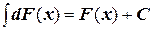
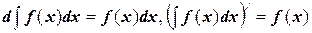
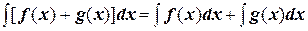
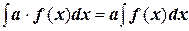
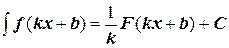
1.1. Основные понятия теории обыкновенных дифференциальных уравнений.
Дифференциальные уравнения (ДУ) являются одним из самых употребительных средств математического моделирования и используются при изучении процессов, в которых участвуют такие величины как скорость и ускорение. Термин "дифференциальное уравнение" принадлежит немецкому математику Готфриду Вильгельму Лейбницу (1676 г.).
Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию y = f(x) и ее производные f '(x), f ''(x), …, f(n)(x).
ДУ в общем виде можно записать так:
Определение 2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Пример.
Определение 3. Решением (интегралом) ДУ называется любая функция y = j(x) которая при подстановке в уравнение (1), превращает его в тождество.
Например, решением уравнения y = f '(x) является функция y = F(x) – первообразная для f(x).
Определение 4. Решение ДУ называется общим, если оно содержит столько произвольных постоянных C1, C2, …, Cn, каков порядок n этого уравнения y = j (x, C1, C2, …, Cn).
Задача. Проверить, будет ли указанная функция являться решением ДУ
Определение 5. Частным решением ДУ называется решение, полученное из общего при различных числовых значениях произвольных постоянных.
Обычно частное решение получают из общего не прямым заданием значений произвольным постоянным C1, C2, …, Cn, а исходя из n начальных условий, которым должно удовлетворять искомое частное решение y = j(x):
Задача нахождения частного решения, удовлетворяющего начальным условиям, называется задачей Коши.
Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой. С геометрической точки зрения общее решение ДУ представляет собой семейство кривых, а частное решение – отдельную кривую этого семейства.
Некоторые задачи, приводящие к составлению дифференциальных уравнений (см. учебник Н.Л. Лобоцкой. Основы высшей математики):
- закон свободных незатухающих колебаний 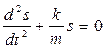 ; m - где масса тела, s - величина смещения тела от положения равновесия, t – время, k – коэффициент упругости;
; m - где масса тела, s - величина смещения тела от положения равновесия, t – время, k – коэффициент упругости;
- закон охлаждения тела 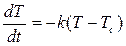 , где Тc – температура окружающей среды, t –время, k – коэффициент пропорциональности, зависящий от физических свойств тела и его геометрической формы,
, где Тc – температура окружающей среды, t –время, k – коэффициент пропорциональности, зависящий от физических свойств тела и его геометрической формы,
- закон размножения бактерий 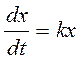 ; k – коэффициент пропорциональности, x - количество бактерий, t - время.
; k – коэффициент пропорциональности, x - количество бактерий, t - время.
- закон роста клеток с течением времени 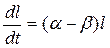 , где l - длина клетки, t – время, α и β – постоянные, характеризующие процессы синтеза и распада.
, где l - длина клетки, t – время, α и β – постоянные, характеризующие процессы синтеза и распада.
1.2. ДУ первого порядка с разделяющимися переменными
Определение 6. Уравнение вида
называется ДУ с разделяющимися переменными. Оно может быть приведено к виду:
Это выражение является общим решением .
Примеры.
1.3. Дифференциальные уравнения второго порядка.
Рассмотрим ДУ вида y '' = f(x,y,y').
Общим решением ДУ второго порядка является функция y = j(x, C1, C2), где С1 и С2 не зависящие от х произвольные постоянные.
Часто встречаются линейные однородные ДУ второго порядка с постоянными коэффициентами вида:
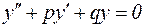 , где pи q– действительные числа
, где pи q– действительные числа
или 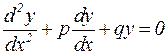 . (1.2)
. (1.2)
В уравнениях (1.2) может быть p=0 или q=0, или p=0 и q=0.
Теорема. Пусть дано ДУ 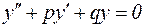 и его характеристическое уравнение имеет вид r2+py+q = 0, тогда при решении этого уравнения возможны три случая:
и его характеристическое уравнение имеет вид r2+py+q = 0, тогда при решении этого уравнения возможны три случая:
1) если корни действительные r1 ≠ r2, то:
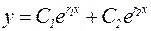 ; (1.3)
; (1.3)
2) если корень один (действительный), т.е. 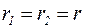 , то:
, то:
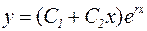 ; (1.4)
; (1.4)
3) если действительных корней нет, т.е. 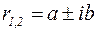 (мнимые или комплексные), то:
(мнимые или комплексные), то:
y= eαx(C1⸱cosβx+ C2⸱sinβx) (1.5)
В уравнении 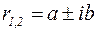 буквой «i» обозначена мнимая единица, квадрат которой равен «-1», т.е.
буквой «i» обозначена мнимая единица, квадрат которой равен «-1», т.е. 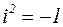 . Например:
. Например: 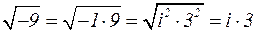 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Вестибулярная сенсорная система | | |
Дата добавления: 2017-10-04; просмотров: 2058;











