Контроль целостности информации

В процессе хранения и передачи информации могут происходить ошибки. Приемнику и передатчику информации необходимо знать, что данные в потоке должны соответствовать определенным правилам. Приводя реальный поток в соответствие с этими правилами, приемник может восстановить его исходное содержание. Количество и типы практически восстановимых ошибок определяются применяемыми правилами кодирования. Всегда существует порог ошибок в сообщении, после которого сообщение не поддается даже частичному восстановлению. Соответствие потока данных тем или иным правилам теория информации описывает как наличие статистических автокорреляций или информационной избыточности в потоке. Такие данные всегда будут больше по объему, чем исходные.

Естественные языки обеспечивают очень высокую (в письменной форме двух- и трехкратную, а в речевой – еще большую) избыточность за счет применения сложных фонетических, лексических и синтаксических правил. Одним из способов повышения избыточности человеческой речи является применение стихов. Но справиться с задачей восстановления такой информации способен лишь человеческий мозг. Поэтому правила кодирования, применяемые в вычислительных системах, должны удовлетворять не только требованиям теоретико-информационной оптимальности, но и быть достаточно просты для программной или аппаратной реализации.

Простейшим способом внесения избыточности является полное дублирование данных. При этом избыточность этого метода слишком велика для большинства применений, а, кроме того, данный метод позволяет только обнаружить ошибку, но не устранить ее. Трехкратное копирование в ряде случаев позволяет не только обнаружить, но и устранить ошибку. Видно, что ряд методов позволяет только обнаружить ошибку, а другие – и восстановить ее. Все данные, с которыми работают современные вычислительные системы, представляют собой последовательности битов, поэтому рассмотрим только такие последовательности.

Простейшим из способов кодирования с обнаружение ошибок – это бит четности. В данном случае блок дополняется битом для того, чтобы общая сумма битов была четной или нечетной. Данный способ позволяет выявить ошибку об одном бите.

Более сложная схема – это CRC (Cycle Redundancy Code) – циклический избыточный код. При вычислении CRC разрядности N выбирают число R требуемой разрядности и вычисляют остаток от деления на R блока данных, сдвинутое влево на N битов. Двоичное число, образованное блоком данных и остатком, делится на R и это можно использовать для проверки целостности блока.

Простой метод кодирования, позволяющий не только обнаруживать, но и устранять ошибки, называется блочной или параллельной четностью и состоит в том, что мы записываем блок данных в виде двухмерной матрицы и подсчитываем бит четности для каждого столбца и каждой строки. При одиночной ошибке, таким образом, легко обнаружить бит, который содержит ошибку.

Широко применяемый код Хэмминга находится в близком родстве с параллельной четностью. Его идея состоит в том, чтобы снабжать каждый блок несколькими битами четности, подсчитанными по различным совокупностям битов данных. Этот код гарантирует обнаружение одиночной ошибки (в отличие от CRC, который имеет всего лишь вероятность обнаружения ошибки). Этот код позволяет устранить одиночную ошибку в блоке. Для работы алгоритма необходимо выполнять соотношение

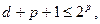
где 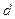– количество битов данных, 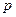– разрядность контрольного кода.

Если это уравнение превращается в равенство, то этот код называют оптимальным кодом Хэмминга.

Часто оказывается выгодно, как это ни странно, сочетать упаковку данных с их избыточным кодированием. При этом достигается уменьшение передаваемой или хранимой информации при условии ее защиты от ошибок ее передачи.