Введение в криптографию

При передаче или хранении данных часто возникает задача защиты информации от нежелательного прочтения. Чаще всего в этом случае используют один из методов криптографии (от греческого тайнопись). В отличие от большинства терминов компьютерной лексики это слово не английского, а греческого происхождения.

История криптографии насчитывает тысячи лет, и многие основополагающие принципы современной криптографии известны, возможно, с доисторических времен, однако, существенный прогресс в теории шифрования был достигнут лишь относительно недавно, в связи с разработкой современной теории информации.

Практически все методы криптографии сводятся к преобразованию данных в набор из конечного количества символов и осуществлению над этими символами двух основных операций: подстановки и перестановки. Подстановка состоит в замене одних символов на другие. Перестановка состоит в изменении порядка символов. В качестве символов при этом могут выступать различные элементы сообщения – так, при шифровании сообщений на естественных языках подстановке и перестановке могут подвергаться как отдельные буквы, так и слова или даже целые предложения (как, например, в аллегорических изложениях магических и священных текстов). В современных алгоритмах этим операциям чаще всего подвергаются блоки последовательных битов. Некоторые методики можно описать как осуществление операции подстановки над полным сообщением. Подстановки и перестановки производятся по определенным правилам. При этом надежда возлагается на то, что эти правила и/или используемые в них параметры известны только автору и получателю шифрованного сообщения и неизвестны посторонним лицам. В докомпьютерную эру старались засекретить обе составляющие процесса шифрования. Сейчас для шифрования, как правило, используют стандартные алгоритмы, секретность же сообщения достигается путем засекречивания используемого алгоритмом параметра, ключа (key). Прочтение секретного сообщения посторонним лицом, теоретически, может быть осуществлено двумя способами: похищением ключевого значения либо его угадыванием путем анализа перехваченной шифровки. Если первое мероприятие может быть предотвращено только физической и организационной защитой, то возможность второго определяется используемым алгоритмом. Ниже мы будем называть процесс анализа шифровки взломом шифра, а человека, осуществляющего этот процесс, – взломщиком. По-научному эта деятельность называется более нейтрально – криптоанализ. К примеру, сообщение на естественном языке, зашифрованное подстановкой отдельных букв, уязвимо для частотного анализа: основываясь на том факте, что различные буквы встречаются в текстах с разной частотой, взломщик легко – и с весьма высокой достоверностью – может восстановить таблицу подстановки. Существуют и другие примеры неудачных алгоритмов, которые сохраняют в неприкосновенности те или иные присутствовавшие в сообщении автокорреляции – каждый такой параметр можно использовать как основу для восстановления текста сообщения или обнаружения ключа.

Устойчивость шифра к поиску автокорреляций в сообщении называется криптостойкостью алгоритма. Даже при использовании удачных в этом смысле алгоритмов, если взломщик знает, что исходные (нешифрованные) данные удовлетворяют тому или иному требованию, например, содержат определенное слово или снабжены избыточным кодом, он может произвести полный перебор пространства ключей: перебирать все значения ключа, допускаемые алгоритмом, пока не будет получено удовлетворяющее требованию сообщение. При использовании ключей достаточно большой разрядности такая атака оказывается чрезмерно дорогой, однако прогресс вычислительной техники постоянно сдвигает границу "достаточности" все дальше и дальше. Так, сеть распределенных вычислений Bovine в 1998 году взломала сообщение, зашифрованное алгоритмом DES с 56-разрядным ключом за 56 часов работы. Простым и эффективным способом борьбы с такой атакой является расширение пространства ключей. Увеличение ключа на один бит приводит к увеличению пространства вдвое – таким образом, линейный рост размера ключа обеспечивает экспоненциальный рост стоимости перебора. Некоторые алгоритмы шифрования не зависят от разрядности используемого ключа – в этом случае расширение достигается очевидным способом. Если же в алгоритме присутствует зависимость от разрядности, расширить пространство можно, всего лишь применив к сообщению несколько разных преобразований, в том числе и одним алгоритмом, но с разными ключами. Еще один способ существенно усложнить работу взломщику – это упаковка сообщения перед шифрованием и/или дополнение его случайными битами. Важно подчеркнуть, впрочем, что количество двоичных разрядов ключа является лишь оценкой объема пространства ключей сверху, и во многих ситуациях эта оценка завышена. Некоторые алгоритмы в силу своей природы могут использовать только ключи, удовлетворяющие определенному условию – например, RSA использует простые числа. Это резко сужает объем работы по перебору, поэтому для обеспечения сопоставимой криптостойкости разрядность ключа RSA должна быть намного больше, чем у алгоритмов, допускающих произвольные ключи. Низкая криптостойкость может быть обусловлена. не только алгоритмом шифрования, но и процедурой выбора ключа: если ключ может принимать любые двоичные значения заданной разрядности, но реально для его выбора используется страдающий неоднородностью генератор псевдослучайных чисел, мы можем значительно сократить объем пространства, которое реально должен будет перебрать взломщик наших сообщений. Еще хуже ситуация, когда в качестве ключа используются легко запоминаемые слова естественного языка: в этом случае реальный объем пространства ключей даже довольно большой разрядности может измеряться всего лишь несколькими тысячами различных значений.

Современные алгоритмы шифрования делятся на два основных класса: с секретным и с публичным ключом.

Алгоритмы с секретным ключом, в свою очередь, делятся на потоковые (stream) и блочные (block). Потоковые алгоритмы обычно используют подстановку символов без их перестановки. Повышение криптостойкости при этом достигается за счет того, что правила подстановки зависят не только от самого заменяемого символа, но и от его позиции в потоке. Примером простейшего – и в то же время абсолютно не поддающегося взлому – потокового алгоритма является система Вернама или одноразовый блокнот. Система Вернама основана на ключе, размер которого равен размеру сообщения или превосходит его. При передаче двоичных данных подстановка осуществляется сложением по модулю 2 (операцией исключающего или) соответствующих битов ключа и сообщения.

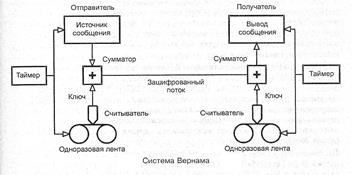
Если ключ порожден надежным генератором случайных чисел (например, правильно настроенным оцифровщиком теплового шума), никакая информация об автокорреляциях в исходном тексте сообщения взломщику не поможет: перебирая полное пространство ключей, взломщик вынужден будет проверить все сообщения, совпадающие по количеству символов с исходным, в том числе и все сообщения, удовлетворяющие предполагаемому автокорреляционному соотношению. Это преимущество теряется, если один и тот же ключ будет использован для кодирования нескольких сообщений: взломщик, перехвативший их все, сможет использовать эти сообщения и предположения об их содержимом при попытках отфильтровать ключ от полезной информации – отсюда и второе название алгоритма. Применение системы Вернама, таким образом, сопряжено с дорогостоящей генерацией и, главное, транспортировкой ключей огромной длины, и поэтому она используется лишь в системах экстренной правительственной и военной связи.

Более практичным оказалось применение в качестве ключа псевдослучайных последовательностей, порождаемых детерминированными алгоритмами. В промежутке между первой и второй мировыми войнами широкое распространение получили шифровальные машины, основанные на механических генераторах таких последовательностей. Чаще всего использовались сочетания, получаемые при вращении колес с взаимно простыми количествами зубцов. Основной опасностью при использовании таких методов шифрования является возможность определить текущую точку последовательности – узнав ее (например, по косвенным признакам догадавшись, что в данной точке сообщения должно быть такое-то слово, и восстановив использовавшийся при ее шифровании элемент ключа), взломщик может продолжить генерацию с той же точки и расшифровать весь дальнейший поток.

В системах цифровой связи широкое применение получили блочные алгоритмы, выполняющие над блоками данных фиксированной длины последовательности – иногда довольно сложные – перестановок, подстановок и других операций, чаще всего двоичных сложений данных с ключом по какому-либо модулю. В операциях используются компоненты ключевого слова относительно небольшой разрядности. Например, широко применяемый блочный алгоритм DES шифрует 64-битные блоки данных 56-битным ключом. Для современной вычислительной техники полный перебор 56-битного пространства возможен, поэтому сейчас все большее распространение получают алгоритмы с большей разрядностью ключа – Blowfish, IDEAL и др.

Шифры с открытым ключом называются также двухключевыми. Если в алгоритмах со скрытым ключом для кодирования и декодирования сообщений используется один и тот же ключ, то здесь используются два ключа: публичный и приватный. Для прочтения сообщения, закодированного публичным ключом, необходим приватный, и наоборот. Помимо обычных соображений криптостойкости, к таким алгоритмам предъявляется дополнительное требование: невозможность восстановления приватного ключа по публичному иначе как полным перебором пространства ключей. Двухключевые схемы шифрования намного сложнее в разработке, чем схемы с секретным ключом: требуется найти преобразование, не поддающееся обращению при помощи применявшегося в нем публичного ключа, но такое, чтобы с применением приватного ключа его все-таки можно было обратить. Известные криптоустойчивые схемы основаны на произведениях простых чисел большой разрядности, дискретных логарифмах и эллиптических кривых. Наиболее широкое применение получил разработанный в 1977 г. алгоритм RSA. Известные двухключевые алгоритмы требуют соответствия ключей весьма специфическим требованиям, поэтому для достижения криптостойкости, сопоставимой с блочными алгоритмами, необходимо использовать ключи намного большей разрядности. Так, снятые в 2000 году ограничения Министерства торговли США устанавливали ограничения разрядности ключа, который мог использоваться в экспортируемом за пределы США программном обеспечении: для схем с секретным ключом устанавливался предел, равный 48 битам, а для схем с открытым – 480. Использование ключей большой разрядности требует значительных вычислительных затрат, поэтому двухключевые схемы чаще всего применяются в сочетании с обычными: обладатель публичного ключа генерирует случайную последовательность битов, кодирует ее и отправляет обладателю приватного ключа. Затем эта последовательность используется в качестве секретного ключа для шифрования данных. При установлении двустороннего соединения стороны могут сначала обменяться своими публичными ключами, а затем использовать их для установления двух разных секретных ключей, используемых для шифрования данных, передаваемых в разных направлениях. Такая схема делает практичной частую смену секретных ключей: так, в протоколе SSH ключ генерируется на каждую сессию, в протоколе виртуальных приватных сетей IPSEC время жизни ключа ограничено восемью часами. Еще более широкое применение двухключевые схемы нашли в области аутентификации и электронной подписи. Электронная подпись представляет собой контрольную сумму сообщения, зашифрованную приватным ключом отправителя. Каждый обладатель соответствующего публичного ключа может проверить аутентичность подписи и целостность сообщения. Это может использоваться для проверки аутентичности как сообщения, так и самого отправителя. Использование в качестве контрольной суммы обычного CRC невозможно, потому что генерация сообщения с заданным CRC не представляет вычислительной сложности. Для применения в электронной подписи были разработаны специальные алгоритмы вычисления контрольных сумм, затрудняющие подбор сообщения с требуемой суммой.

Загрузка программ

Поскольку программа представляет из себя набор машинных кодов, требуется рассмотреть процедуру ее загрузки в оперативную память компьютера (многие из обсуждаемых далее концепций, впрочем, в известной мере применимы и к прошивке программы в ПЗУ).

Для начала предположим, что программа была заранее собрана в некий единый самодостаточный объект, называемый загрузочным или загружаемым модулем. В ряде операционных систем программа собирается в момент загрузки из большого числа отдельных модулей, содержащих ссылки друг на друга.

Для того чтобы не путаться, давайте будем называть программой ту часть загрузочного модуля, которая содержит исполняемый код. Результат загрузки программы в память будем называть процессом или, если нам надо отличать загруженную программу от процесса ее исполнения, образом процесса. К образу процесса иногда причисляют не только код и данные процесса (подвергнутые преобразованию как в процессе загрузки, так и в процессе работы программы), но и системные структуры данных, связанные с этим процессом. В старой литературе процесс часто называют задачей.

В системах с виртуальной памятью каждому процессу обычно выделяется свое адресное пространство, поэтому мы иногда будем употреблять термин процесс и в этом смысле. Впрочем, во многих системах значительная часть адресных пространств разных процессов перекрывается – это используется для реализации разделяемого кода и данных. В рамках одного процесса может исполняться один или несколько потоков или нитей управления.

Некоторые системы предоставляют и более крупные структурные единицы, чем процесс. Например, в системах семейства Unix существуют группы процессов, которые используются для реализации логического объединения процессов в задания (job). Ряд систем имеют также понятие сессии – совокупности всех заданий, которые пользователь запустил в рамках одного сеанса работы. Впрочем, соответствующие концепции часто плохо определены, а их смысл сильно меняется от одной ОС к другой.

В более старых системах и в старой литературе называют результат загрузки задачей, а процессами – отдельные нити управления. Однако в наиболее распространенных ныне ОС семейств Unix и Win32, принято задачу называть процессом, а процесс – нитью (tread).