Принцип Даламбера для точки и системы материальных точек.
При движении материальной точки в любой момент времени приложенные к ней активные силы и реакции связей вместе с силой инерции образуют систему сил, эквивалентную нулю (уравновешенную систему сил)
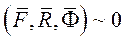
|
В соответствии с аксиомами статики основное уравнение движения материальной точки имеет вид
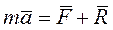
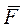 - равнодействующая активных сил,
- равнодействующая активных сил, 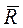 - равнодействующая реакций связей.
- равнодействующая реакций связей.
Запишем уравнение в виде
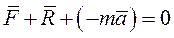
Слагаемое 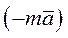 обозначают
обозначают 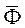 и называют даламберовой силой инерции (или просто силой инерции).
и называют даламберовой силой инерции (или просто силой инерции).
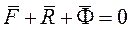
|
При движении механической системы в любой момент времени приложенные силы и реакции связей вместе с силами инерции образуют систему сил, эквивалентную нулю.
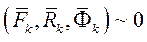
|
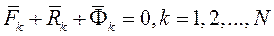 (I)
(I)
Суммируя левые части по всем точкам
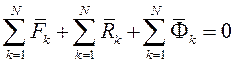
Умножив каждое уравнение векторно слева на радиус-вектор 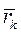 k-й точки и просуммировав их, имеем:
k-й точки и просуммировав их, имеем:
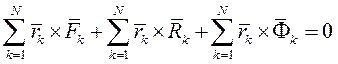
или
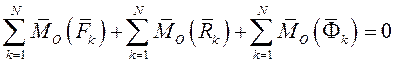
Если силы, приложенные к k-й точке системы, разложить на внешнюю и внутреннюю, а не на активные и реакции связей, то
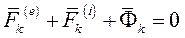
Так как главный вектор и главный момент относительно произвольного центра приведения внутренних сил системы равен нулю, то
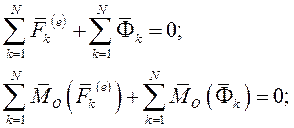
Дата добавления: 2021-07-22; просмотров: 505;











