Упражнения для самостоятельной работы

1. Постройте графики следующих функций:
1) , , , ;
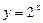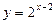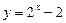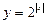2) , , , , , ;
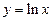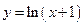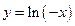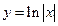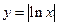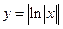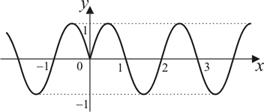
3) , , , , , ;
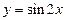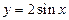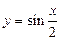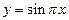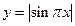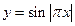4) , , .

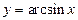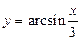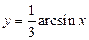2. Докажите справедливость следующих равенств:
1) ;
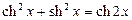2) ;
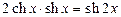3) ;
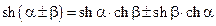4) .

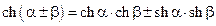Ответы к упражнениям для самостоятельной работы

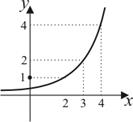
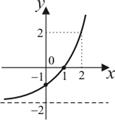
1.	1)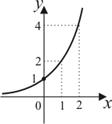
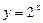
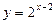
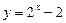
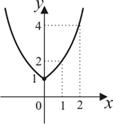
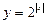
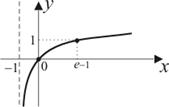
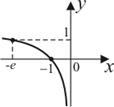
	2)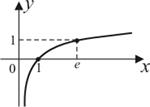
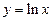
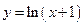
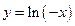
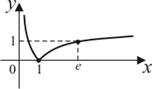
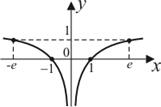
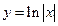
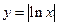
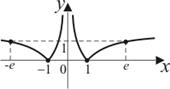
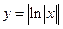
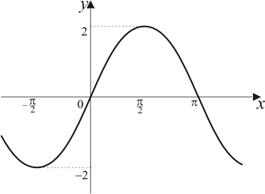
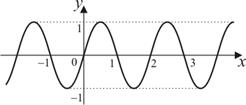
	3)
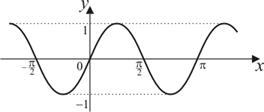
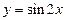
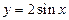
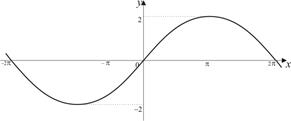
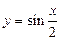
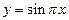
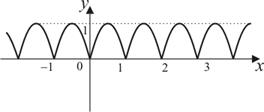
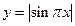
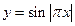
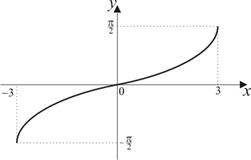
	4)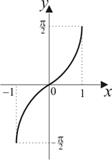

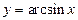
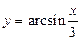
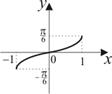
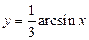
Вопросы для самопроверки

Что такое постоянная функция?

Что такое степенная функция?

Что такое показательная функция?

Что такое логарифмическая функция?

Что такое тригонометрические функции?

Что такое обратные тригонометрические функции?

Что такое гиперболические функции?

Что называется степенной функцией?

Что называется показательной функцией?

Что такое логарифмическая функция?

Что называется логарифмом числа х по основанию а?

Что такое натуральные логарифмы?

Что называется экспонентой?

Что такое обратные тригонометричекие функции?

Что такое арккосинус х?

Что такое арксинус х?

Что такое арктангенс х?

Что такое арккотангенс х?

Что такое гиперболические функции?

Что такое гиперболический синус?

Что такое гиперболический косинус?

Что такое гиперболический тангенс?

Что такое гиперболический котангенс?

Что такое основное тождество для гиперболических функций?

Глоссарий

арккосинус х это…(стр. 138)

арккотангенс х это…(стр. 138)

арксинус х это…(стр. 138)

арктангенс х это…(стр. 138)

гиперболические функции это…(стр. 130)

гиперболические функции это…(стр. 139)

гиперболический косинус это... (стр. 139)

гиперболический котангенс это…(стр. 140)

гиперболический синус это…(стр. 139)

гиперболический тангенс это…(стр. 140)

логарифмическая функция это…(стр. 133)

логарифмическая функция это…(стр. 130)

логарифмом числа х по основанию а называется…(стр. 133)

натуральные логарифмы это…(стр. 134)

обратные тригонометричекие функции это…(стр. 137)

обратные тригонометрические функции это…(стр. 130)

основное тождество для гиперболических функций это…(стр. 140)

основными преобразованиями графика 140 называется…(стр. 140)

показательная функция это…(стр. 130)

показательной функцией называется…(стр. 132)

постоянная функция это…(стр. 130)

степенная функция это…(стр. 130)

степенной функцией называется…(стр. 131)

тригонометрические функции это…(стр. 130)

экспонентой называется…(стр. 134)