Натуральные логарифмы
Натуральные логарифмы— это логарифмы по основанию е, где 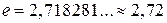 — иррациональное число. Обозначаются
— иррациональное число. Обозначаются 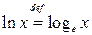 .
.
Основное свойство функции «натуральный логарифм» состоит в том, что касательная к графику функции 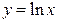 в его точке
в его точке 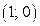 наклонена к оси OX под углом 45°, (рис. 67). Соответствующая этой функции обратная функция
наклонена к оси OX под углом 45°, (рис. 67). Соответствующая этой функции обратная функция 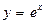 называется экспонентой. Графики обеих взаимно обратных функций
называется экспонентой. Графики обеих взаимно обратных функций 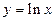 и
и 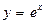 приведены на рис. 68.
приведены на рис. 68.
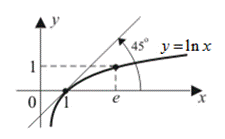 Рис. 67
Рис. 67
| 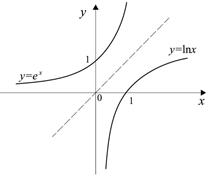 Рис. 68
Рис. 68
|
Тригонометрические функции
Основными тригонометрическими функциями называются следующие четыре функции: 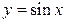 ,
, 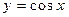 ,
, 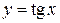 ,
, 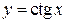 . Их графики приведены на рис. 69.
. Их графики приведены на рис. 69.
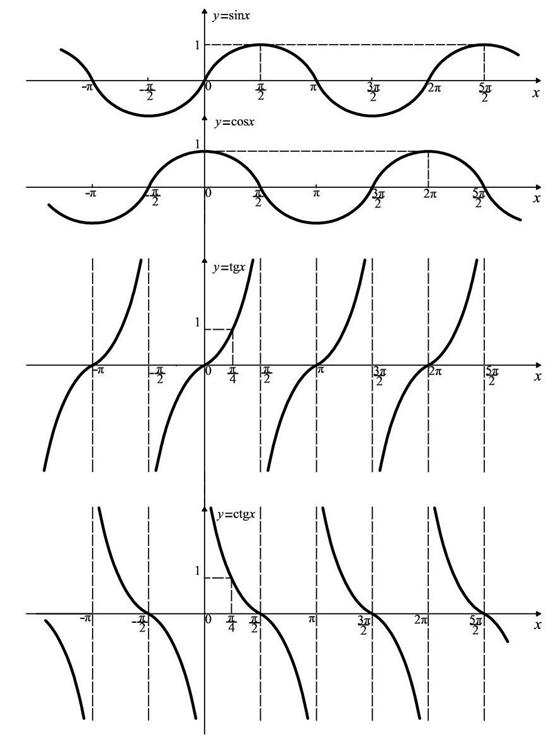
Рис. 69
Для определения основных тригонометрических функций используется тригонометрический круг, (рис. 70).
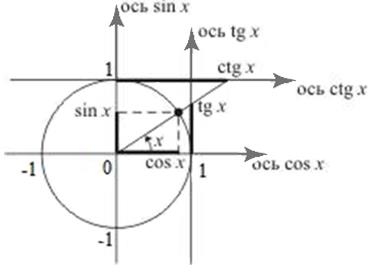 Рис. 70
Рис. 70
| ООФ:
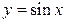 , , 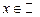 ; ;
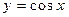 , , 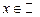 ; ;
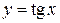 , ,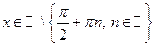 ; ;
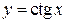 , , 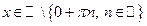 .
ОЗФ: .
ОЗФ:
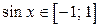 ; ; 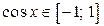 ; ;
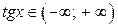 ; ;
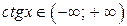 . .
|
Основным отличительным свойством тригонометрических функций является их периодичность:
для 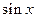 и
и 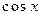 – наименьший период
– наименьший период 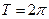 ;
;
для 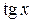 и
и 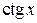 — наименьший период
— наименьший период 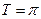 .
.
Основные формулы, связывающие тригонометрические функции
1. Для функций одного аргумента: 
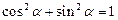
| 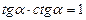
| 
|
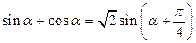
| 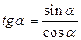
| 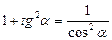
|
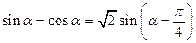
| 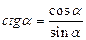
| 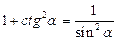
|
2. Для функций аргумента кратности 2:
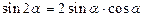
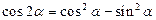
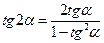
| 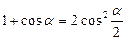
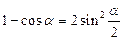
| 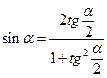
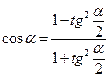
|
3. Для функций существенно различных аргументов
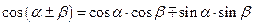
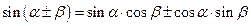
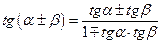
| 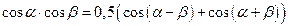
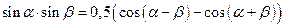
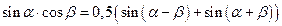
|
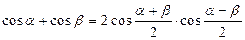 ; ; 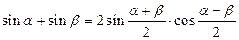
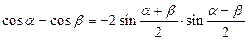 ; ; 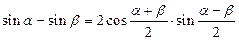
|
Дата добавления: 2021-07-22; просмотров: 578;











